Grade 8 Measure of central tendency: Mean, median, mode for ungrouped data week 1 #math8 #matatag
Summary
TLDRIn this mathematics tutorial, the presenter explains the concept of central tendency, focusing on how to calculate the mean, median, and mode for ungrouped data. Using a set of example scores, the video walks viewers through each step of the calculation, starting with the mean (average), followed by the median (middle value), and finally the mode (most frequent value). The video also includes a multiple-choice activity and a practical question about averages. The presenter encourages viewers to practice and offers solutions at the end, aiming to help students better understand central tendency in statistics.
Takeaways
- 😀 The video introduces the concept of central tendency, which includes the mean, median, and mode for ungrouped data.
- 😀 The mean is the most commonly used measure of central tendency and is calculated by summing all data points and dividing by the number of data points.
- 😀 To calculate the mean, sum the individual scores and divide by the total number of scores in the data set.
- 😀 The median is the middle value in a sorted data set, and can be found by arranging the data in ascending or descending order.
- 😀 When the data set has an odd number of values, the median is the middle value, but when the number is even, the median is the average of the two middle values.
- 😀 The mode is the most frequently occurring value in a data set, and in cases with more than one mode, the data set is considered bimodal or multimodal.
- 😀 If there is no repetition of values in the data set, then there is no mode.
- 😀 A practical example was given using a set of data where the mode was found to be 8, as it appeared the most frequently.
- 😀 The video explains how to handle situations with multiple modes, either bimodal or multimodal, when two or more values repeat with the same frequency.
- 😀 A multiple-choice question was used to illustrate how the mean, median, and mode can be calculated for a given set of data to determine which statement is true.
- 😀 The video concludes with a problem-solving activity where viewers were encouraged to compute the necessary grade for Anna to achieve an average of 78 after four tests.
Q & A
What is the definition of 'mean' in statistics?
-The mean is the most commonly used measure of central tendency, calculated by adding all the data points and dividing by the total number of data points.
How do you calculate the mean for ungrouped data?
-To calculate the mean for ungrouped data, sum all the individual data points and then divide the sum by the total number of data points.
What is the formula used to calculate the mean?
-The formula for the mean is represented as x̄ = Σxi / n, where x̄ is the mean, Σxi is the sum of all the data points, and n is the total number of data points.
How do you calculate the median for ungrouped data?
-To calculate the median, first arrange the data points in ascending or descending order. If the number of data points is odd, the median is the middle value. If it is even, the median is the average of the two middle values.
What should you do if the set of data has an even number of points when calculating the median?
-If the data set has an even number of points, you calculate the median by averaging the two middle values after arranging the data in order.
What does the term 'mode' refer to in statistics?
-The mode refers to the most frequently occurring value in a data set. A set may have one mode (unimodal), two modes (bimodal), or more modes (multimodal).
Can a data set have no mode? If so, give an example.
-Yes, a data set can have no mode if no value repeats. For example, the data set {1, 2, 3, 4, 5} has no mode because all values occur only once.
What is the mode of the data set {2, 4, 4, 5, 7, 8, 8, 8, 11, 12}?
-The mode of the data set is 8, as it appears three times, more frequently than any other value.
What does it mean when a data set is described as 'bimodal'?
-A data set is bimodal if it has two modes, meaning two values appear with the same highest frequency. For example, {4, 4, 8, 8, 10} is bimodal, with modes of 4 and 8.
In the example problem about Anna's grades, how do you calculate the grade needed on the fourth test to achieve an average of 78?
-To achieve an average of 78, you need to calculate the total sum required for four tests, which is 78 * 4 = 312. Since the sum of the first three grades (86, 68, 79) is 233, Anna needs to score 79 on the fourth test to reach the target average.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Ukuran Pemusatan Data Kelompok

Statistika Dasar Ukuran Pemusatan Data (Mean, Modus, Median) Data Tunggal dan Data Kelompok

UKURAN PEMUSATAN DATA BERKELOMPOK | Rataan Median Modus Kuartil Desil Persentil

Statistika - Ukuran Pemusatan Data (Mean, Median, Modus)
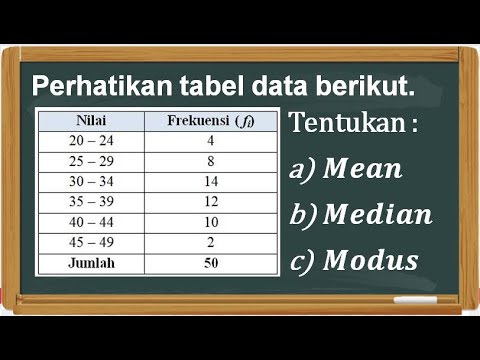
Menentukan Mean, Median, dan Modus Data Kelompok

STATISTIKA: Ukuran gejala pusat dan ukuran letak 1
5.0 / 5 (0 votes)
