Pembahasan Latihan Soal Busur Lingkaran - Matematika SMA Kelas XI Kurikulum Merdeka
Summary
TLDRIn this educational video, the presenter explains how to solve a circle arc length problem. The scenario involves a circle with points A and B, a given central angle of 120 degrees, and a radius of 18 cm. The video walks viewers through the process of calculating the length of the minor arc AB using a formula. After analyzing the given data, the presenter demonstrates how to substitute values into the formula and simplify to get the final result: 12π cm. The video aims to help viewers understand and solve similar problems with clarity and confidence.
Takeaways
- 😀 The video explains how to calculate the length of an arc in a circle using a given central angle and radius.
- 😀 The problem involves a circle with points A and B on the circumference, and the central angle between them is 120°.
- 😀 The radius of the circle is given as 18 cm, and the objective is to find the length of the minor arc AB.
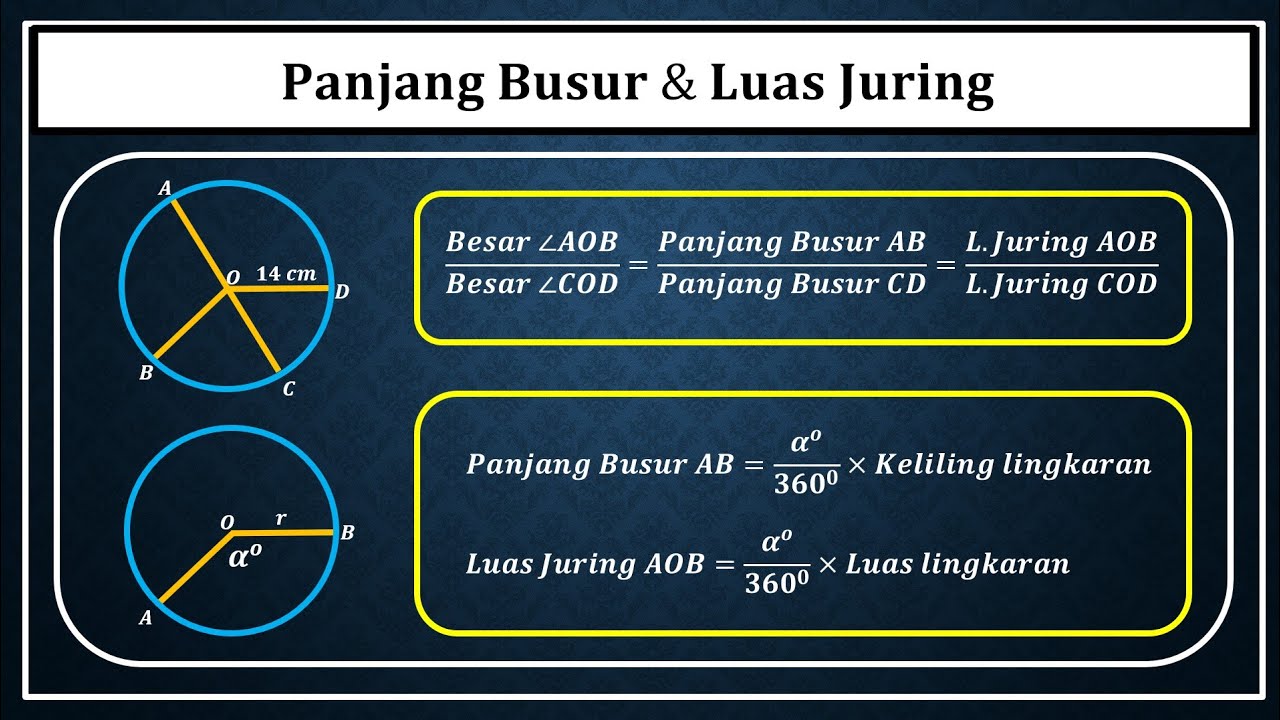
- 😀 The formula to calculate the length of an arc is: Arc Length = (A / 360°) × 2πr.
- 😀 The central angle A is 120°, and the radius r is 18 cm, which are substituted into the arc length formula.
- 😀 The angle 120° is simplified as 120/360 = 1/3, which is then used in the formula to calculate the arc length.
- 😀 The formula becomes (1/3) × 2 × 18 × π, simplifying to 12π cm as the length of the arc.
- 😀 The correct answer is 12π cm, which corresponds to option C in the provided multiple-choice answers.
- 😀 The presenter emphasizes the importance of simplifying fractions and keeping π as is (not replacing with 3.14 or 22/7).
- 😀 The video concludes by thanking the viewers for participating and encouraging them to keep practicing and stay motivated in their studies.
Q & A
What is the main topic of the video?
-The video explains how to solve a problem related to finding the length of an arc in a circle.
What are the given values in the problem?
-The given values in the problem are a central angle of 120° and a radius of 18 cm.
What formula is used to find the length of an arc?
-The formula used is: Arc length = (θ / 360°) * 2πr, where θ is the central angle and r is the radius.
How is the central angle used in the formula?
-The central angle (θ) is used to find the fraction of the circle that the arc represents by dividing it by 360°, the total degrees in a circle.
What is the value of the central angle in the given problem?
-The value of the central angle is 120°.
How is the radius represented in the formula?
-The radius is represented as 'r' in the formula, and in this problem, it is given as 18 cm.
Why is π (pi) not substituted with a numerical value in the answer?
-Pi (π) is not substituted with a numerical value because the options in the answer choices include π, so it is kept as π for consistency.
What does the simplification of 120/360 result in?
-The simplification of 120/360 results in 1/3.
What is the final length of the arc AB?
-The final length of the arc AB is 12π cm.
How does the simplification of the expression help in solving the problem?
-Simplifying the fraction 120/360 to 1/3 makes the calculation easier, as it reduces the complexity of the expression and allows for quick multiplication to find the arc length.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)