Panjang Busur dan Luas Juring Lingkaran

Summary

In this tutorial video, the presenter explains how to calculate the area of a sector and the length of an arc in a circle. The formulas for these calculations are demonstrated with two examples: one where the angle and radius are provided, and another using known arc lengths. The video covers essential concepts like the relationship between the angle, radius, and the resulting sector or arc measurements, providing clear and easy-to-follow steps to ensure understanding. It aims to help viewers confidently solve problems related to circle geometry.

Takeaways

• 😀 The video introduces the concepts of arc length and sector area in a circle.
• 😀 It explains two sets of formulas used to calculate these values based on different problem scenarios.
• 😀 Formula Set 1 is used when two angles, arc lengths, or sector areas are given.
• 😀 Formula Set 2 is used when only one angle and the radius are given.
• 😀 The formula for the area of a sector is: (Angle/360) * π * r², where 'Angle' is the central angle and 'r' is the radius.
• 😀 The formula for the length of an arc is: (Angle/360) * 2 * π * r, where 'Angle' is the central angle and 'r' is the radius.
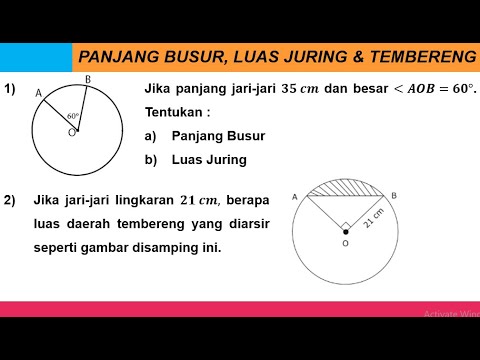
• 😀 In the first example, the sector area is calculated using a 90° angle and a radius of 14 cm, resulting in an area of 154 cm².
• 😀 The length of the arc for the same problem is calculated as 22 cm.
• 😀 In the second example, the area of a sector is calculated using given arc lengths and a known sector area (48 cm²), resulting in an area of 120 cm² for another sector.
• 😀 The script emphasizes simplifying fractions and applying the correct formula depending on the given information.
• 😀 The video concludes with the host thanking the viewers and inviting them to engage with the channel through likes, subscriptions, and comments.

Q & A

What are the two main formulas used in the video to calculate arc length and sector area?

The two main formulas used in the video are: 1) For sector area: (Alfa degrees / 360 degrees) * π * r², where Alfa is the central angle in degrees and r is the radius of the circle. 2) For arc length: (Alfa degrees / 360 degrees) * 2 * π * r, where Alfa is the central angle in degrees and r is the radius of the circle.

When should you use the first formula in the video?

The first formula should be used when the problem provides either two arc lengths, two sector areas, or two central angles.

What is the significance of the 90/360 simplification in the video?

The 90/360 simplification is used to reduce the ratio of the central angle (90 degrees) to the full circle (360 degrees) in order to simplify the calculations. It simplifies to 1/4.

Why was π set to 22/7 in the video example?

π was set to 22/7 in the video because the radius (14) is a multiple of 7, making 22/7 the appropriate approximation of π for easier calculations.

How do you calculate the sector area when the radius is given as 14 cm?

To calculate the sector area, first use the formula (Alfa / 360) * π * r². For Alfa = 90 degrees and r = 14 cm, this becomes (90/360) * 22/7 * 14², which simplifies to 154 cm².

What is the correct approach to calculating the arc length in the video?

The correct approach to calculating the arc length is using the formula (Alfa / 360) * 2 * π * r. For a 90-degree angle and radius of 14 cm, the arc length is calculated as (90/360) * 2 * 22/7 * 14, resulting in an arc length of 22 cm.

What does the term 'juring' refer to in the context of the video?

'Juring' refers to a sector of a circle in the context of the video. It represents the area bounded by two radii and the arc of the circle.

What is the significance of using 360 degrees in the formulas?

The 360 degrees in the formulas is used because a full circle has 360 degrees. The formula calculates a fraction of the total area or arc length based on the central angle.

What should you do when the problem involves two arc lengths, as seen in the example?

When the problem involves two arc lengths, you should use the first formula, which involves cross-multiplying the known arc lengths with the corresponding sector areas, as demonstrated in the second part of the video.

What is the final result of calculating the area of sector AOB in the video?

The final result for the area of sector AOB is 154 cm², based on the given radius of 14 cm and a central angle of 90 degrees.