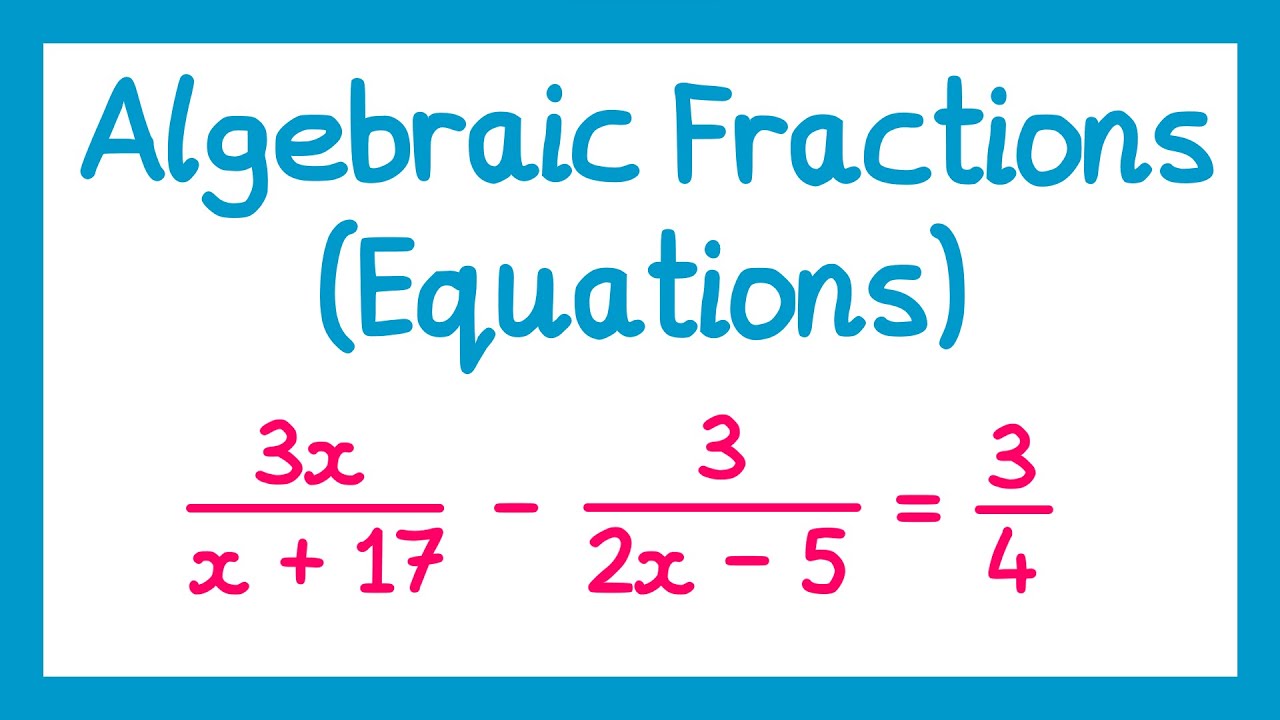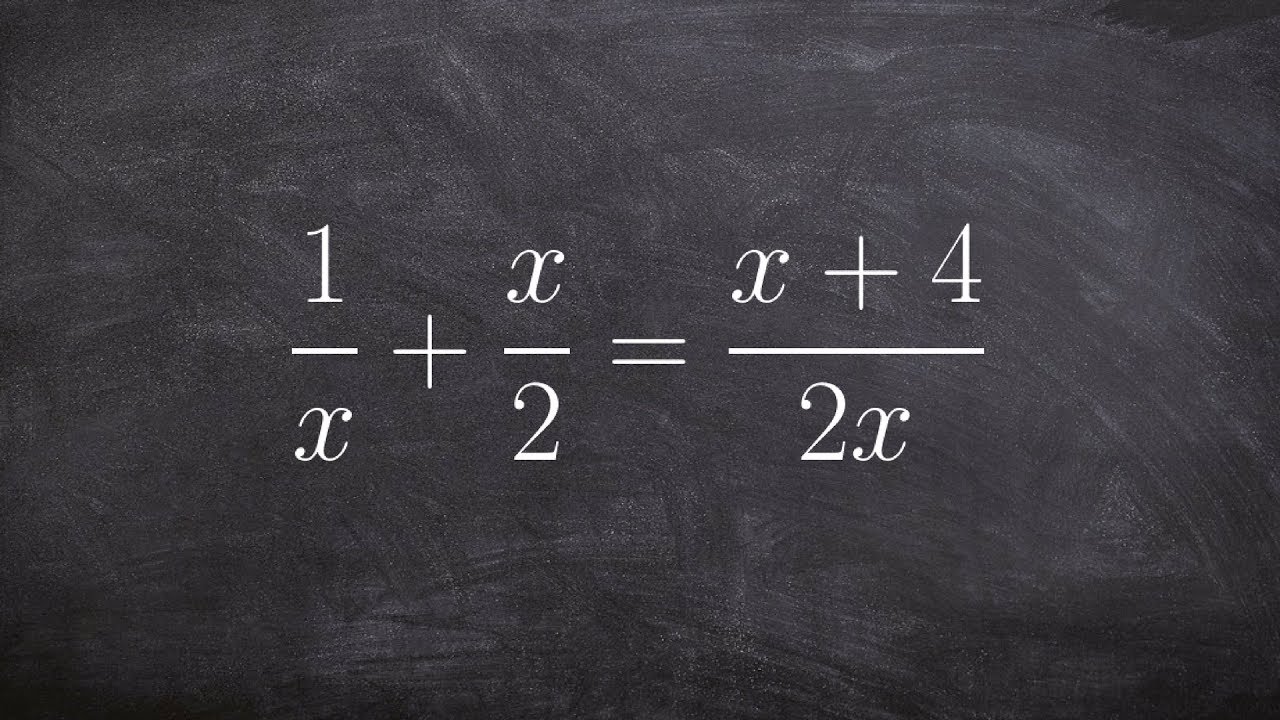Rational Equations

Summary

This instructional video script focuses on solving rational equations, which are equations involving fractions with variables. The approach emphasized is to gather all fractions on one side with a common denominator before proceeding with the solution. The script explains the importance of avoiding division by zero and provides step-by-step examples to illustrate the process of finding a common denominator and solving for the variable. It also highlights the significance of excluding values that would result in a zero denominator. The examples gradually increase in complexity, demonstrating how to handle different scenarios, including when denominators are factored or when there are no additions or subtractions involved. The goal is not only to solve the equations but also to prepare for tackling rational inequalities and graphing rational functions.

Takeaways

• 🧩 Rational equations involve fractions with variables, also known as rational expressions.
• ❌ Division by zero is undefined in mathematics, which is a crucial concept when solving rational equations.
• 🔍 If the numerator of a fraction is zero and the denominator is not zero, the expression evaluates to zero.
• 🚫 Exclude values that would make the denominator zero, as these cannot be solutions to the equation.
• 📚 Finding a common denominator is essential for combining fractions and solving rational equations.
• 📉 Rational equations can be solved by moving all fractions to one side of the equation and setting the sum equal to zero.
• 🔢 Factoring can simplify the process of finding a common denominator, especially when denominators can be factored.
• 📌 Multiplying the numerator and denominator of a fraction by the same non-zero expression does not change its value.
• 📝 When subtracting fractions, ensure that the entire numerator of the fraction being subtracted is accounted for.
• 🔑 Solutions to rational equations must not result in division by zero, so check the solutions against the excluded values.
• 📉 In cases where the solutions do not satisfy the original equation, it indicates there is no solution.

Q & A

What is a rational equation?

A rational equation is an equation that contains rational expressions, which are fractions with variables in the numerator and/or denominator.

Why should we avoid dividing by zero when solving rational equations?

Division by zero is undefined in mathematics. If the denominator of a rational expression is zero, the expression itself becomes undefined, which means we cannot have a solution that results in division by zero.

How does the value of zero affect the numerator and denominator of a fraction?

If the numerator of a fraction is zero, the entire expression evaluates to zero, regardless of the denominator (as long as it's not zero). However, if the denominator is zero, the expression is undefined.

What is the purpose of finding a common denominator when solving rational equations?

Finding a common denominator allows us to combine all the fractions in the equation into a single fraction, which simplifies the process of solving the equation by making it easier to isolate the variable.

What technique does the video suggest for solving rational equations, and why?

The video suggests getting all the fractions together on one side with a common denominator. This approach is used because it is also applicable to solving rational inequalities and graphing rational functions, making it a versatile technique.

What are the excluded values for the potential solution in the first example equation x - 4 / (2ar * 3x + 1) over (2x to the 3 power * 5x - 4) equals 0?

The excluded values are x = 0 and x = 4/5 because these values would make the denominator equal to zero, which is not allowed.

How do we solve the equation 5/x + 1 = 3x/(x + 1)?

We get all the fractions on one side by subtracting 3x/(x + 1) from both sides, combine the fractions since they have a common denominator, and then solve for x by setting the numerator equal to zero and ensuring the denominator is not zero.

What is the solution to the equation 6/x = -2/(x - 4)?

The solution is x = 3, as it is the value that makes the numerator zero without making the denominator zero.

How does the video approach solving rational inequalities?

The video mentions that the same technique used for solving rational equations will be applied to rational inequalities, although it does not go into detail on how this is done.

What is a shortcut mentioned in the video for finding a common denominator?

A shortcut mentioned is to factor the denominators that can be factored, which can simplify the process of finding a common denominator.

What is the solution to the equation 6/x = 11/(3x + 8)?

The solution is x = 7/24, after finding a common denominator and solving for x by setting the numerator equal to zero.