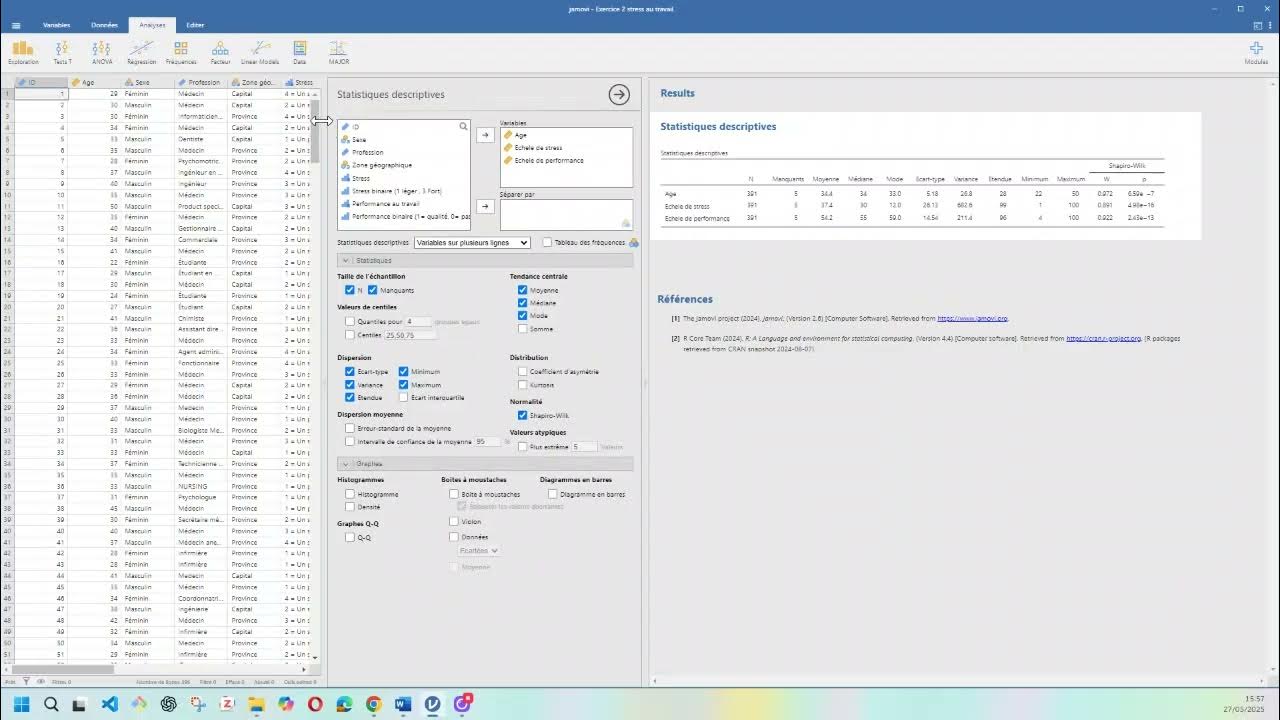
✅ Information cachée derrière : Moyenne, Médiane, Variance, Écart type
Summary
TLDRDans cette vidéo, l'orateur explique l'importance des indicateurs de dispersion, tels que la variance et l'écart type, pour mesurer la dispersion des données autour de la moyenne. À travers un exemple pratique avec les notes d'élèves, il montre comment ces mesures permettent de mieux comprendre la variabilité des scores, contrairement à la moyenne et à la médiane qui ne fournissent pas cette information. Le calcul de la variance et de l'écart type est également détaillé, soulignant comment ces deux indicateurs offrent des perspectives claires sur l'homogénéité ou la dispersion des données dans une classe.
Takeaways
- 😀 La variance et l'écart type sont des indicateurs de dispersion qui mesurent l'étendue des données autour de la moyenne.
- 😀 La moyenne est simplement la somme des valeurs divisée par le nombre total d'élèves, mais elle ne donne pas d'information sur la répartition des scores.
- 😀 La médiane est la valeur centrale qui sépare les données en deux parties égales, mais elle n'indique pas non plus la dispersion des données.
- 😀 Les valeurs de variance et d'écart type montrent combien les données sont éloignées de la moyenne et permettent de comparer les dispersions entre différentes classes.
- 😀 La variance est calculée en élevant au carré les écarts par rapport à la moyenne, ce qui peut exagérer les différences extrêmes.
- 😀 L'écart type est la racine carrée de la variance, ce qui permet de ramener l'échelle à une unité plus compréhensible et plus proche des valeurs originales.
- 😀 Même si deux classes ont la même moyenne et médiane, la dispersion des notes peut être très différente, ce que la variance et l'écart type révèlent clairement.
- 😀 Dans l'exemple donné, la classe 1 a une grande dispersion (variance de 18) alors que la classe 2 a une faible dispersion (variance de 2), bien que les deux aient une moyenne et une médiane de 11.
- 😀 Les calculs de la variance et de l'écart type sont essentiels pour comprendre la variabilité des données et pour comparer différents ensembles de données.
- 😀 L'écart type fournit une mesure plus intuitive de la dispersion des données, en raison de sa racine carrée, par rapport à la variance qui est exagérée à cause des carrés des écarts.
Q & A
Qu'est-ce que la variance et pourquoi est-elle importante ?
-La variance est une mesure de la dispersion des valeurs d'un ensemble de données. Elle est importante car elle permet de quantifier l'écart moyen des valeurs par rapport à la moyenne, indiquant ainsi à quel point les valeurs sont réparties autour de la moyenne.
Quel est le lien entre la variance et l'écart-type ?
-L'écart-type est la racine carrée de la variance. Tandis que la variance mesure l'écart au carré, l'écart-type ramène cette mesure à l'unité d'origine des données, rendant ainsi l'interprétation plus intuitive.
Dans l'exemple des notes des élèves, pourquoi la moyenne et la médiane sont-elles égales à 11 ?
-Dans l'exemple des notes des élèves, les notes sont suffisamment symétriques autour de 11, ce qui fait que la moyenne (la somme des notes divisé par le nombre d'élèves) et la médiane (la valeur centrale) sont égales à 11.
Comment la variance permet-elle de comparer deux groupes avec des moyennes identiques ?
-Même si deux groupes ont la même moyenne, la variance permet de mesurer leur dispersion. Un groupe avec une variance plus élevée indique une plus grande dispersion autour de la moyenne, tandis qu'une faible variance suggère des valeurs plus proches de la moyenne.
Pourquoi les calculs de variance peuvent-ils donner des résultats exagérés ?
-La variance peut donner des résultats exagérés car les différences entre les valeurs et la moyenne sont élevées au carré, ce qui accentue les écarts importants. Cela peut rendre la mesure moins représentative de la dispersion réelle des données.
Comment la médiane est-elle déterminée dans cet exemple ?
-La médiane est déterminée en identifiant la valeur qui divise les données en deux parties égales. Dans l'exemple, la médiane est 11, car deux élèves ont des notes supérieures et deux ont des notes inférieures à 11.
Quel est l'avantage de l'écart-type par rapport à la variance ?
-L'écart-type est souvent préféré car il ramène la mesure de la dispersion à la même unité que les données d'origine, ce qui le rend plus facile à interpréter que la variance, qui est exprimée en unités au carré.
Pourquoi est-il important de comprendre l'écart-type et la variance dans l'analyse des données ?
-L'écart-type et la variance permettent de mieux comprendre la répartition des données. Tandis que la moyenne ou la médiane donnent une idée générale du centre des données, ces mesures de dispersion offrent un aperçu de la variabilité ou de l'homogénéité des valeurs.
Dans l'exemple des deux classes, quelle différence observe-t-on dans la dispersion des notes ?
-La première classe présente une grande dispersion des notes, avec une variance de 18 et un écart-type de 4,2. En revanche, la deuxième classe a une faible dispersion avec une variance de 2 et un écart-type de 1,4. Cela montre que les élèves de la deuxième classe ont des notes plus proches de la moyenne.
Que signifie un écart-type de 4,2 dans cet exemple ?
-Un écart-type de 4,2 signifie que, en moyenne, les notes des élèves de la première classe diffèrent de la moyenne de 4,2 points. Cela donne une idée de l'amplitude des écarts entre les notes des élèves par rapport à la moyenne.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)