Chapter 8: Piecewise Interpolation (Part 1 - Introduction)
Summary
TLDRIn this video, we explore chapter 8 on piecewise interpolation, focusing on spline functions. The chapter introduces how piecewise interpolation can overcome the oscillatory behavior of high-degree polynomials. It covers different spline types: zero-order (constant), first-order (linear), second-order (quadratic), and third-order (cubic), each offering varying levels of smoothness and continuity in their derivatives. The video explains the construction and application of these splines, highlighting how they can be used to approximate complex functions with stability and accuracy, making them ideal for large datasets.
Takeaways
- 😀 Piecewise interpolation is a method that improves the stability of interpolation when working with large datasets, avoiding the oscillations caused by high-degree polynomials.
- 😀 Spline interpolation uses polynomials defined on sub-intervals, providing smoother and more accurate interpolation than traditional polynomial methods.
- 😀 The order of the spline polynomial does not depend on the number of data points but on the desired smoothness of the interpolation.
- 😀 Spline functions are constructed on intervals between consecutive data points, known as 'knots,' where the function must pass through each data point.
- 😀 A spline of degree 0 is a piecewise constant function, providing no smoothness or continuity in its derivatives.
- 😀 A spline of degree 1 is a piecewise linear function, which connects data points with straight lines. It has a continuous first derivative but is not smooth at the data points.
- 😀 A spline of degree 2 is a piecewise quadratic function that ensures continuity of the first derivative but lacks smoothness at the data points.
- 😀 A spline of degree 3 is a piecewise cubic function, where both the first and second derivatives are continuous, making the function smooth at the data points.
- 😀 Higher-degree splines (especially cubic splines) provide more accurate and smoother approximations of the true function, especially when working with real-world data.
- 😀 Piecewise interpolation allows for the use of lower-degree polynomials, which can significantly reduce computational complexity while maintaining accuracy.
Q & A
What is piecewise interpolation?
-Piecewise interpolation is a method of approximating a function by using simpler polynomials over smaller subintervals. This approach avoids the oscillatory behavior of high-degree polynomials by keeping the degree of the interpolating polynomial low.
What is the primary advantage of piecewise interpolation over polynomial interpolation?
-The primary advantage of piecewise interpolation is that it avoids the highly oscillatory behavior that can occur when using high-degree polynomials with large datasets. It uses lower-degree polynomials on smaller subintervals, resulting in more stable and smoother approximations.
What are splines in the context of piecewise interpolation?
-Splines are piecewise polynomials used to approximate a function over subintervals. They are constructed to ensure a specified level of continuity between adjacent pieces, making the overall approximation smooth and well-behaved.
What is a spline of degree 0, and how is it constructed?
-A spline of degree 0 is a piecewise constant function, where the function value remains constant over each subinterval. It is constructed by simply assuming that the function takes a constant value on each subinterval between the data points.
How does a piecewise linear spline differ from a piecewise constant spline?
-A piecewise linear spline connects each pair of data points with straight lines, providing a linear interpolation between the points. In contrast, a piecewise constant spline simply assigns a constant value to the function on each subinterval without any variation between points.
What is the main difference between a piecewise quadratic spline and a piecewise cubic spline?
-A piecewise quadratic spline uses a quadratic polynomial on each subinterval, while a piecewise cubic spline uses a cubic polynomial. The cubic spline provides more flexibility, ensuring both the first and second derivatives are continuous across the subintervals, resulting in a smoother interpolation.
What is the significance of ensuring continuity of derivatives in spline interpolation?
-Ensuring continuity of derivatives in spline interpolation is crucial for maintaining smooth transitions between subintervals. It prevents abrupt changes in the function's behavior and ensures that the spline behaves smoothly across the entire domain, particularly in terms of its slope and curvature.
Why is a cubic spline often preferred over linear or quadratic splines?
-A cubic spline is often preferred because it provides a smoother and more accurate interpolation. It ensures continuity of both the first and second derivatives, which results in better approximations of real-world data and is capable of modeling more complex functions with curvature.
What is the role of 'knots' in spline interpolation?
-Knots are the data points where the spline must pass through. They are the points that define the subintervals, and the spline is constructed such that the interpolation passes through these points while maintaining the required level of derivative continuity.
How does a cubic spline perform when approximating the Runga function in the provided example?
-In the provided example, the cubic spline approximation of the Runga function closely matches the actual derivative of the function. This demonstrates how cubic splines can effectively capture the curvature of a function and provide highly accurate derivative approximations.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
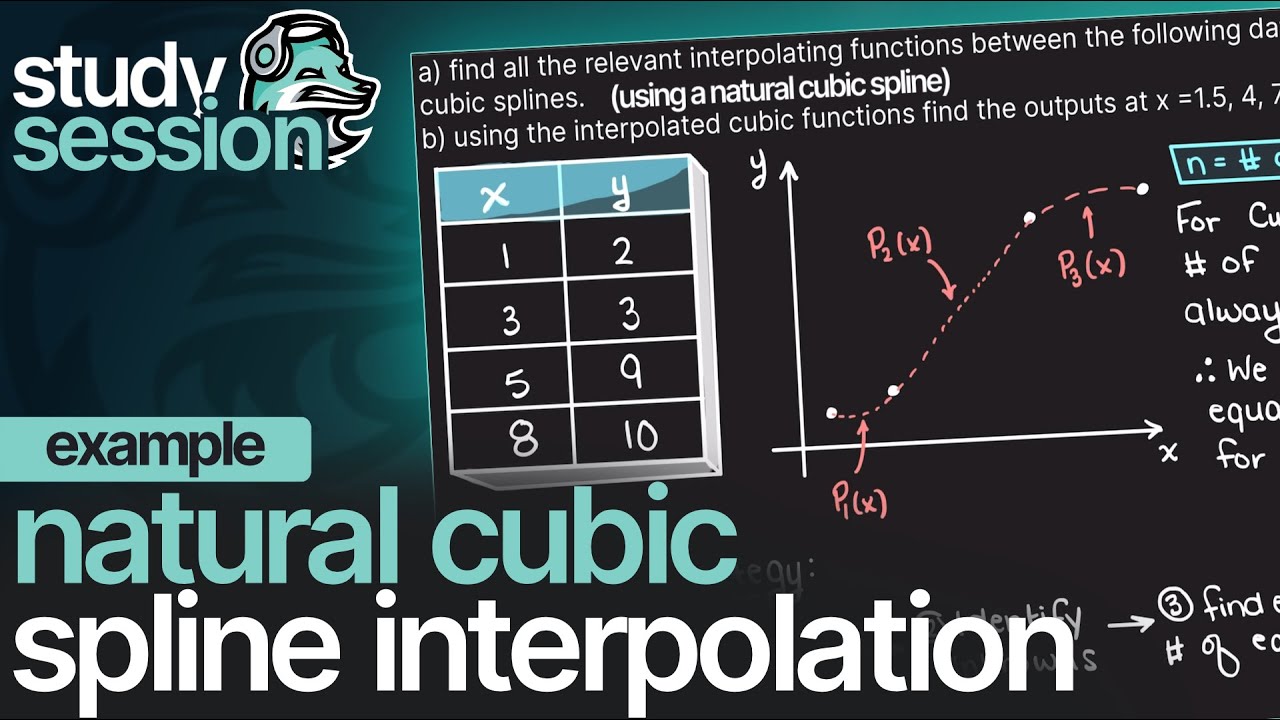
Natural Cubic Spline Interpolation Example | Numerical Methods

Evaluate a Piecewise Function | Eat Pi

FUNGSI PIECEWISE || PRESENTASI KELOMPOK 5 XI 13-SMASTA

Graphing Piecewise Functions, Domain & Range - Limits, Continuity, & Absolute Value ,

Laplace Transform and Piecewise or Discontinuous Functions

Fungsi Tangga , Matematika Lanjut Kelas XI Semester 4, oleh Ranty Aditya Aggriamurti, S.Pd.
5.0 / 5 (0 votes)
