Equations Reducible to Exact by Integrating Factors
Summary
TLDRThe video discusses various methods and rules related to solving differential equations, with a focus on integration techniques such as finding the integrating factor and multiplying equations. It also touches on rules for transforming equations into exact forms and solving them using different approaches. While the main focus is on mathematical principles, the transcript includes some unrelated references and informal content, adding a unique flavor to the tutorial. The speaker encourages viewers to engage with additional resources and continue learning about these advanced mathematical concepts.
Takeaways
- 😀 Rule #1 for solving differential equations involves multiplying by an integrating factor to simplify and solve the equation.
- 😀 Multiple methods can be used to handle different types of differential equations, often involving integration and multiplication.
- 😀 There is an emphasis on the importance of an integrating factor, which helps in solving linear differential equations.
- 😀 The script discusses several rules that aid in solving differential equations, including Rule #2, which seems to involve flexibility in applying different approaches.
- 😀 The transcript mentions the importance of 'multiplying by the original' equation to transform it into an exact differential equation.
- 😀 Rule #6 is noted as not being applicable in certain cases, but no specific context is given for its restrictions.
- 😀 The script briefly touches on rules and formulas for integrating differential equations but does not go into full detail on each rule.
- 😀 The discussion includes references to real-world applications like fluid dynamics, but the technical details are less clear in this part of the script.
- 😀 The use of subscription-based content is mentioned, indicating that the video or script may be part of a tutorial or educational platform.
- 😀 The transcript references 'Doremon' and 'Buddhist devotion,' suggesting an eclectic mix of topics, but the connection to the main subject of differential equations is unclear.
Q & A
What is the primary focus of the transcript?
-The transcript primarily focuses on methods for solving differential equations, including the use of integration factors, multiplication of equations, and the application of specific mathematical rules for transforming equations.
What is the concept of an integration factor in solving differential equations?
-An integration factor is a mathematical function that is multiplied to a differential equation to make it easier to solve, often by simplifying the equation or making it exact.
How do the 'rules' mentioned in the transcript relate to solving differential equations?
-The 'rules' refer to specific methods or strategies that are applied to manipulate or transform differential equations in order to solve them more efficiently. For example, one rule may be to multiply the equation by an integrating factor.
What is the significance of the reference to 'Rule Number One' in the transcript?
-Although not fully explained in the transcript, 'Rule Number One' seems to refer to a fundamental approach for solving differential equations, likely involving the integration factor or another key method.
What does the phrase 'multiplying the original equation' refer to in the context of differential equations?
-Multiplying the original equation refers to the process of applying a transformation, such as multiplying the equation by an integrating factor or another function, to simplify or make the equation solvable.
Why is the 'function of 21 and 2010' mentioned in the transcript?
-The 'function of 21 and 2010' might be part of an example illustrating how to apply certain mathematical rules or transformations to solve a differential equation. It could be part of a specific case study mentioned in the video.
What is meant by 'exact differential equations' as mentioned in the transcript?
-Exact differential equations are those for which an integrating factor can make them solvable by direct integration. These equations have the property that they can be written in a form where a potential function exists.
How does the concept of 'subscript' come into play in the solving process?
-The mention of 'subscript' likely refers to the notation used in differential equations to identify specific terms or variables within the equation. This can help in organizing and manipulating the equation more clearly.
What is the role of the term 'multiplied differential equation' in the context of solving these equations?
-The term 'multiplied differential equation' likely refers to the process of multiplying the differential equation by a factor (like an integrating factor) to simplify or make the equation solvable by standard methods.
What might 'subscribing for more videos from search engines' imply in the transcript?
-This appears to be a call to action, encouraging viewers to subscribe for more educational content on solving differential equations or related topics, likely hosted on a video platform or educational website.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

S. Y. B. SC. (Comp.Sci.) (Paper - II: Numerical Techniques) Ch1-Algebraic & Transcendental Eq.(Lec1)
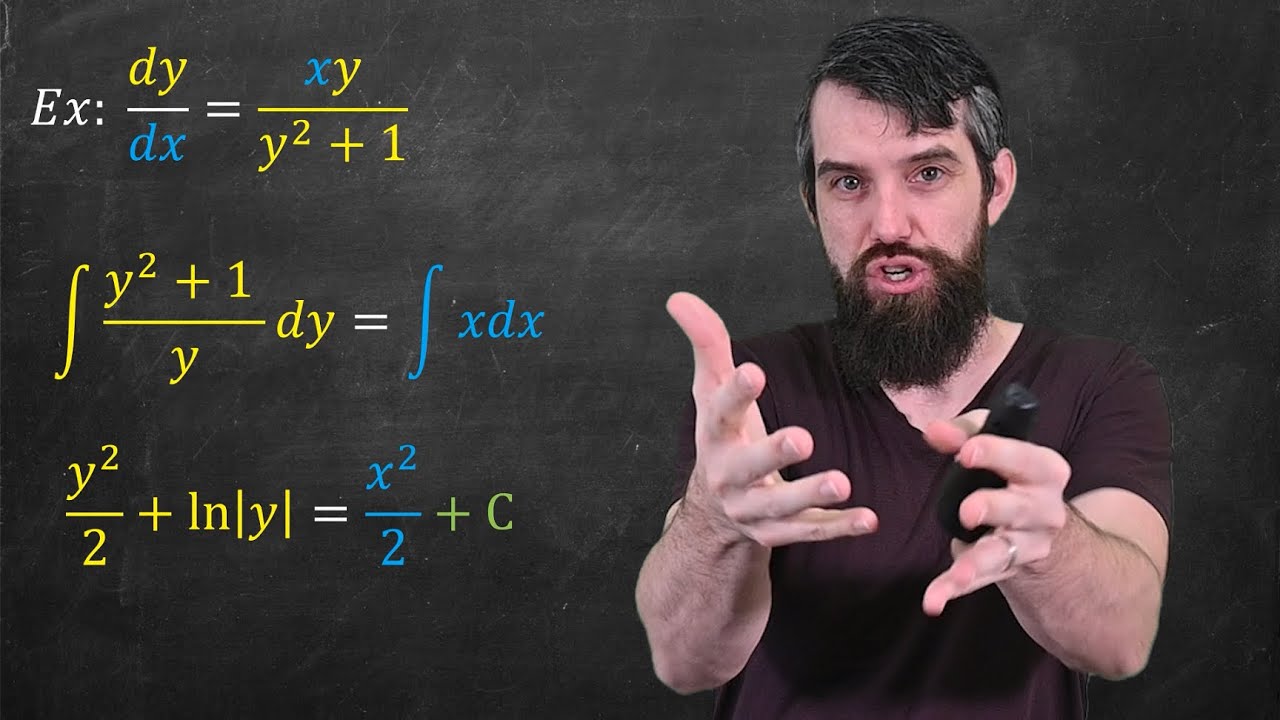
Separation of Variables // Differential Equations

Finalizando a semana 3

Differential Equation | Reducible Exact Differential Equation PART 3 - Concept & Example By GP Sir

Introducing Weird Differential Equations: Delay, Fractional, Integro, Stochastic!

Solving Polynomial Equations By Factoring and Using Synthetic Division
5.0 / 5 (0 votes)
