Solving Logarithmic Equations
Summary
TLDRThis lesson focuses on solving basic logarithmic equations, covering key concepts like converting logarithmic forms to exponential ones, using the change of base formula, and applying logarithmic properties. It explores various examples, from simple equations like log base 2 of 16 to more complex ones involving natural logs, quadratic equations, and logarithms with multiple terms. The video emphasizes strategies for simplifying logarithmic expressions, factoring quadratics, and solving for unknown variables in both logarithmic and exponential forms. Through detailed examples, viewers learn how to handle both straightforward and challenging logarithmic problems effectively.
Takeaways
- 😀 Logarithmic equations can be solved by converting them into exponential form, allowing for easier manipulation and solving.
- 😀 For example, log base 2 of 16 equals x can be rewritten as 2^x = 16, and solved by recognizing that 2^4 = 16, so x = 4.
- 😀 The change of base formula (log(a) / log(b)) can be used to find logarithmic values when a direct conversion to exponential form is difficult.
- 😀 When solving equations like log base x of 81 = 4, converting to exponential form (x^4 = 81) allows you to solve for x by taking the fourth root.
- 😀 In some cases, solving logarithmic equations may require using fractional exponents, like when working with expressions such as 32^(4/5) to find the value of x.
- 😀 The natural logarithm (ln) has a base of e, and solving equations involving ln can be done by converting them to exponential form (e^7 = x).
- 😀 Logarithmic equations can sometimes result in quadratic equations, which can be solved using factoring, as shown in equations like log base 3 of (5x + 2) = log base 3 of (7x - 8).
- 😀 When solving equations with logarithms on both sides, like log base 2 of (x^2 + 4x) = log base 2 of 5, you can equate the expressions inside the logs and solve the resulting quadratic equation.
- 😀 The properties of logarithms, such as log(a) + log(b) = log(ab) and log(a) - log(b) = log(a/b), are useful for simplifying and solving logarithmic expressions.
- 😀 Some equations involve extraneous solutions, which must be checked to ensure the solution is valid, as negative numbers inside a logarithm are not allowed.
Q & A
What is the first step when solving a logarithmic equation like log base 2 of 16 equals x?
-The first step is to convert the logarithmic equation to its exponential form. In this case, log base 2 of 16 equals x is converted to 2^x = 16.
How can we solve for x when log base 2 of 16 equals x?
-We know that 2^4 = 16, so x equals 4.
What is the change of base formula used in logarithmic equations?
-The change of base formula is log_b(a) = log(a) / log(b), where you can calculate logarithms in any base using common logarithms (base 10).
How do you solve log base x of 81 equals 4?
-Convert the equation to exponential form: x^4 = 81. Then, take the fourth root of both sides to find x = 3.
How do you solve log base 32 of x equals 4/5?
-First, convert to exponential form: 32^(4/5) = x. Find the fifth root of 32, which is 2, and then raise it to the fourth power to get x = 16.
What is the process for solving a logarithmic equation involving a natural logarithm (ln)?
-For ln(x) = 7, the base is e, so convert it to exponential form: e^7 = x. This gives x = e^7, which is approximately 1096.65.
What happens if a logarithmic equation has the same base on both sides?
-If the bases are the same, you can set the expressions inside the logs equal to each other and solve for the variable.
What does the equation log base 7 of (x^2 + 3x + 9) = 2 mean?
-Convert to exponential form: 7^2 = x^2 + 3x + 9. This becomes 49 = x^2 + 3x + 9. Subtract 9 from both sides to get x^2 + 3x = 40, then solve the quadratic equation.
How do you check for extraneous solutions in logarithmic equations?
-After finding potential solutions, substitute them back into the original logarithmic equation. If any result in a negative number inside a logarithm, discard them as extraneous solutions.
What do you do if you have an equation like log base 2 of (x^2 + 4x) = log base 2 of 5?
-Since the bases are the same, set the expressions inside the logs equal: x^2 + 4x = 5. Solve the quadratic equation x^2 + 4x - 5 = 0 to find the solutions x = -5 and x = 1.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
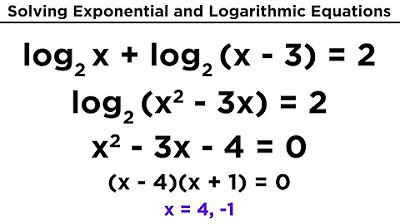
Solving Exponential and Logarithmic Equations

Logarithmic Functions | Transforming Logarithmic Equation to Exponential Form and Vice Versa

Persamaan Logaritma Matematika Peminatan Kelas 10 oleh m4thlab

Logaritmo: Introdução Parte 1 (Aula 1 de 14)
SOLVING LOGARITHMIC INEQUALITIES | GRADE 11 GENERAL MATHEMATICS Q1

Solving Logarithmic Inequalities | General Mathematics
5.0 / 5 (0 votes)
