Calculando valores Z
Summary
TLDREl video ofrece una explicación detallada sobre los valores Z y la distribución normal. Se describe cómo la curva en forma de campana está simétrica y cómo se representa la media en el centro. Los valores Z miden la distancia en términos de desviaciones estándar de la media hacia un punto dado, con desviaciones positivas a la derecha y negativas a la izquierda. Se explica que el área bajo la curva es del 100% y cómo se divide en partes iguales, con el 50% a cada lado de la media. A través de la tabla de Z, se demuestra cómo calcular probabilidades para diferentes valores Z, como el 34% entre la media y una desviación estándar, y el 68% entre -1 y 1. Además, se calcula la probabilidad del 95% para los valores entre -1.96 y 1.96, y se describe cómo encontrar la probabilidad para valores Z menores o mayores que 1.96, que corresponde al 5% restante dividido en dos colas de la distribución.
Takeaways
- 📊 La distribución normal es una curva en forma de campana con una media en el centro.
- 📌 Los valores Z miden la distancia en desviaciones estándar entre la media y un punto dado.
- ➡️ El lado derecho de la curva representa desviaciones estándar positivas, y el izquierdo, negativas.
- 🔴 El área debajo de la curva de la distribución normal es del 100%.
- 🟢 La mitad derecha y la mitad izquierda de la curva son simétricas, cada una con un 50%.
- 🔵 Al medir una desviación estándar desde la media (0), la porción de la curva correspondiente es del 34%.
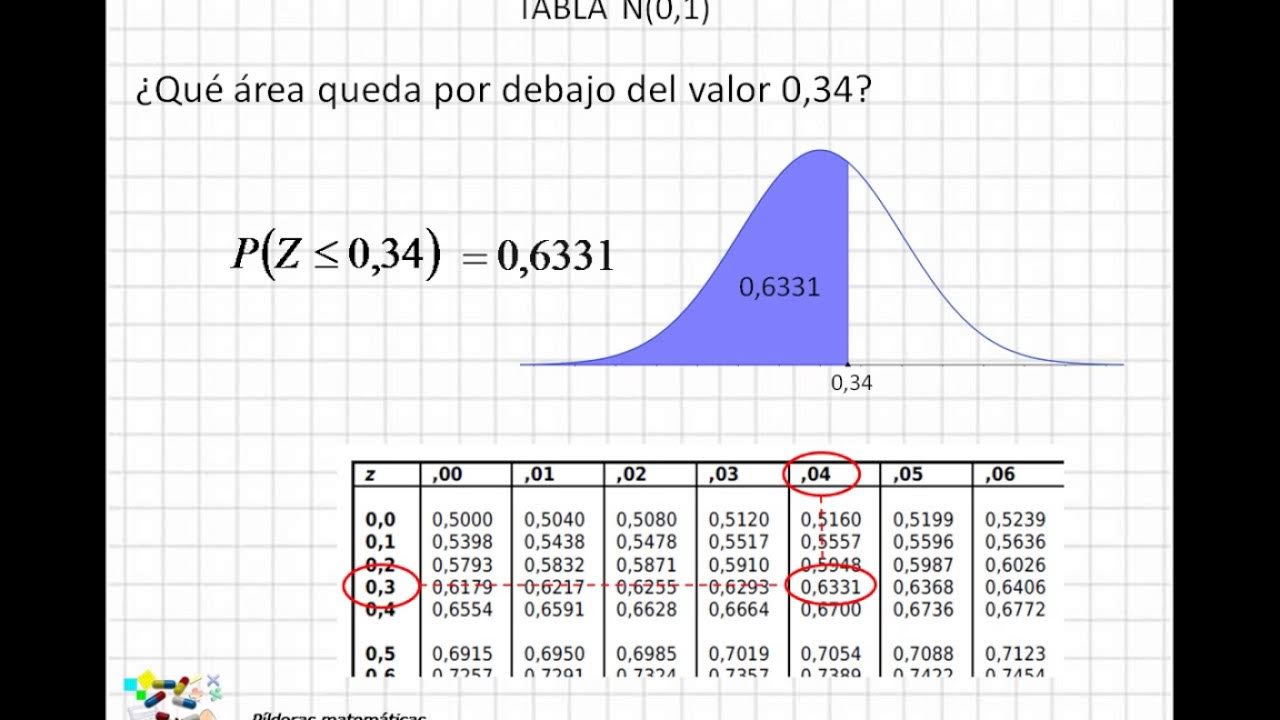
- 🔍 Utilizando una tabla de Z, se pueden encontrar probabilidades asociadas a valores Z específicos.
- 🟠 Un valor Z de 1 corresponde a un 68% de probabilidad entre -1 y 1 en la distribución.
- 📜 Para Z = 1.96, la probabilidad entre 0 y 1.96 (o entre -1.96 y 0) es del 47.5%.
- 🤔 Al sumar las probabilidades de Z = 1.96, obtenemos un 95% de probabilidad entre -1.96 y 1.96.
- 🚫 El 5% restante se divide en dos, con 2.5% en cada cola de la distribución, para Z < -1.96 y Z > 1.96.
Q & A
¿Qué representa la curva en forma de campana en la distribución normal?
-La curva en forma de campana representa la distribución de los datos en una distribución normal, donde la mayoría de los valores se concentran alrededor de la media y disminuyen en frecuencia a medida que se alejan de ella.
¿Cómo se miden los valores Z en la distribución normal?
-Los valores Z se miden en términos de distancias estándar entre la media y el punto escogido, representando la desviación estándar de ese punto respecto a la media.
¿Cuál es la relación entre las desviaciones estándar y los valores Z positivos y negativos?
-Los valores Z positivos representan desviaciones estándar a la derecha de la media, mientras que los valores Z negativos representan desviaciones estándar a la izquierda de la media.
¿Por qué la curva de la distribución normal es simétrica?
-La curva es simétrica porque la distribución normal es una distribución de probabilidad continua que se asume que se distribuye de manera uniforme en ambos lados de la media.
¿Cuál es el porcentaje de la curva que cubre desde la media hasta una desviación estándar?
-El 34% de la curva de la distribución normal cubre desde la media hasta una desviación estándar.
¿Cómo se encuentra el porcentaje asociado a un valor Z en una tabla de Z?
-Se busca el valor de Z en la primera columna de la tabla, luego se localiza la correspondiente 'ordenada superior' en la parte superior de la tabla, y se lee el valor correspondiente, que se convierte en porcentaje.
¿Cuál es la probabilidad de encontrar un valor entre -1 y 1 en la distribución normal?
-La probabilidad de encontrar un valor entre -1 y 1 en la distribución normal es del 68%.
Si Z es igual a 1.96, ¿cuál es la probabilidad de que un valor esté entre 0 y 1.96 en la distribución normal?
-La probabilidad de que un valor esté entre 0 y 1.96 cuando Z es igual a 1.96 es del 47.5%.
¿Cuál es el porcentaje de probabilidad que cubre el rango entre -1.96 y 1.96 en la distribución normal?
-El 95% de la distribución normal cubre el rango entre -1.96 y 1.96.
Si se busca la probabilidad de una observación que caiga por fuera de -1.96 y 1.96 en la distribución normal, ¿qué porcentaje representa esto?
-La probabilidad de una observación que caiga por fuera de -1.96 y 1.96 es del 5%, que se divide en dos partes iguales en las colas de la distribución (2.5% a cada lado).
¿Cómo se interpreta el 5% restante después de cubrir el 95% de la curva de la distribución normal con -1.96 y 1.96?
-El 5% restante se encuentra en las colas de la distribución, más allá de -1.96 y 1.96, y representa los valores que son muy lejanos de la media, considerándose extremos o outliers.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)