Apa itu Pasar Monopoli?
Summary
TLDRThis video delves into the concept of monopoly in microeconomics, contrasting it with perfect competition. It defines monopoly as a market structure dominated by a single seller with significant price-making power. Key topics include the determination of optimal pricing and production, the effects of market power, and the causes of monopolies, such as resource control and government regulation. Additionally, it discusses the social costs associated with monopolies, like deadweight loss and rent-seeking behavior, emphasizing the need for effective government intervention and antitrust laws to promote fair competition and protect consumer welfare.
Takeaways
- 😀 Monopolies are characterized by a single seller in the market, which allows them to set prices and exert market power.
- 📉 In contrast to perfect competition, where both buyers and sellers are price takers, monopolies act as price makers.
- 📊 The demand curve for a monopolistic market is downward sloping, meaning that as prices increase, the quantity demanded decreases.
- 🔍 Marginal revenue (MR) is always less than average revenue (AR) in a monopoly due to the necessity to lower prices to sell additional units.
- 💰 To maximize profit, monopolists produce where marginal revenue equals marginal cost (MR = MC).
- 🧮 The Lerner index is used to measure a monopolist's market power, calculated as the difference between price and marginal cost divided by the price.
- 🏭 Several factors determine the strength of a monopoly's power, including demand elasticity, the number of firms in the market, and the level of competition among firms.
- 📈 Monopolies can exist due to government regulations, patent protections, or because they control essential resources.
- ⚖️ Social costs of monopolies include higher prices, reduced output, and deadweight loss, leading to decreased economic welfare compared to perfect competition.
- 🚨 Governments can regulate monopolies through price controls or antitrust laws to promote competition and prevent market abuses.
Q & A
What is the primary focus of the educational video on the inscribed circle in a triangle?
-The primary focus is to explain the concept of an inscribed circle within a triangle and how to calculate its radius.
How is the radius of the inscribed circle related to the area of the triangle?
-The radius of the inscribed circle can be calculated using the formula: radius = Area / s, where 's' is the semi-perimeter of the triangle.
What formula is used to calculate the area of a triangle?
-The area of a triangle can be calculated using various formulas, such as Heron's formula, which is Area = sqrt(s * (s - a) * (s - b) * (s - c)), where 'a', 'b', and 'c' are the lengths of the sides.
What is the significance of the inscribed circle in geometry?
-The inscribed circle is significant as it represents the largest circle that can fit inside the triangle, touching all three sides, and plays a crucial role in various geometric constructions.
What is the semi-perimeter of a triangle?
-The semi-perimeter 's' of a triangle is half the sum of its side lengths, calculated as s = (a + b + c) / 2.
How does the concept of the inscribed circle apply to real-world scenarios?
-The concept of the inscribed circle can be applied in various fields such as architecture, design, and urban planning, where efficient use of space is essential.
What are some common misconceptions about inscribed circles?
-A common misconception is that the inscribed circle is always centered at the triangle's centroid, while it is actually centered at the incenter, which is determined by the angle bisectors.
How can understanding inscribed circles improve problem-solving in geometry?
-Understanding inscribed circles can enhance problem-solving skills by providing insights into triangle properties and relationships, enabling better reasoning in geometric proofs.
What role does the incenter play in relation to the inscribed circle?
-The incenter is the point where the angle bisectors of a triangle intersect and serves as the center of the inscribed circle.
Can all types of triangles have an inscribed circle?
-Yes, all types of triangles (acute, obtuse, and right) can have an inscribed circle, as long as they have a well-defined area.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Monopolies vs. perfect competition | Microeconomics | Khan Academy

STRUKTUR PASAR

Episode 29: Monopolistic Competition

classification of market monopoly monopolistic competition oligopoly duopoly in telugu
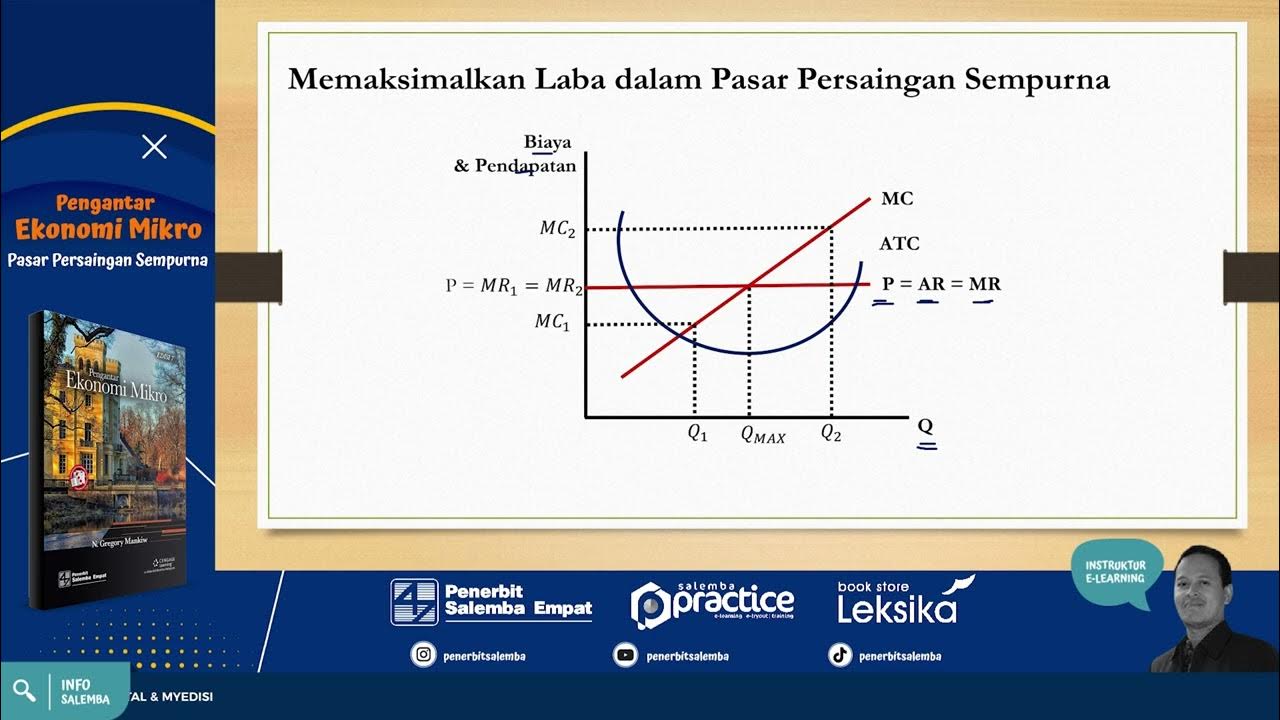
Pasar Persaingan Sempurna -Pengantar Ekonomi Mikro- #soaldanpembahasan #elearningplatform

CFA® Level I Economics - Characteristics of Market Structure
5.0 / 5 (0 votes)
