Math 251 - What is a limit?
Summary
TLDRIn this Math 251 lesson, the concept of limits in calculus is introduced. The instructor breaks down the formal definition, explaining how a function's values approach a certain real number 'l' as the input 'x' approaches a specific value 'a'. Using both graphical and tabular examples, the lesson illustrates how to determine limits, even when the function is undefined at 'x=a', emphasizing the importance of the function's behavior around 'a' rather than at the point itself.
Takeaways
- 📘 The concept of a limit in calculus is introduced, focusing on how function values approach a certain number.
- 📐 A function f(x) must be defined on an interval containing a point 'a', except possibly at 'a' itself.
- 🔢 The limit 'l' is a real number that represents the y-value the function approaches as x approaches 'a'.
- 📉 As x values get closer to 'a', the corresponding f(x) values should get closer to 'l'.
- 📊 The limit is symbolized as 'lim (x→a) f(x) = l', indicating f(x) approaches l as x approaches a.
- 📈 An example is given with a quadratic graph to illustrate how to find the limit as x approaches a specific value.
- 📋 Even with a table of values, the concept of a limit can be applied to determine what the function values approach.
- 🚫 The function does not need to be defined at the point 'a'; it's acceptable to have a 'hole' at that point.
- 📌 The limit exists and is valid even if the function is undefined at the point where x is approaching.
- 👋 The video concludes with a reminder that there are more lessons to follow on this topic.
Q & A
What is the primary focus of the lesson in the transcript?
-The lesson focuses on explaining the concept of limits in calculus, specifically what it means for the limit of a function f(x) to approach a value l as x approaches a certain point a.
How is the definition of a limit presented in the lesson?
-The definition of a limit is presented as a function f(x) being defined at all points in an open interval containing a, except possibly at a itself, with the function values approaching a real number l as x values approach a.
What does it mean for a function to be defined at all values in an open interval containing a?
-It means the function is defined throughout the interval except possibly at the point a, allowing for a 'hole' at that point without affecting the limit.
Why is it okay for the function to have a hole at point a?
-Having a hole at point a is acceptable because the definition of a limit only requires the function to be defined in an interval around a, not necessarily at a itself.
What is the symbolic representation of a limit as x approaches a?
-The symbolic representation of a limit as x approaches a is written as 'lim (x→a) f(x) = l', indicating that f(x) approaches l as x approaches a.
How does the lesson use a graph to illustrate the concept of a limit?
-The lesson uses a graph to show that as x values get closer to a, the corresponding y values (f(x)) get closer to a specific real number l, which is the limit.
What is an example of finding a limit using a graph provided in the lesson?
-An example is finding the limit as x approaches 6 on a quadratic graph, where it's observed that as x values approach 6 from both sides, the y values approach 2.
How can you determine a limit when given a table of values instead of a graph?
-With a table, you look at how the y values (f(x)) change as the x values approach the point of interest from both sides to see if they consistently approach a certain value l.
What does it mean if the function is undefined at the point x equals a?
-If the function is undefined at x equals a, it means there is a hole or a discontinuity at that point, but it does not prevent the existence of a limit as x approaches a.
What is the significance of the y value in the context of limits?
-The y value is significant because it represents the value that the function f(x) approaches as x approaches a certain point a, which is the essence of the limit concept.
How does the lesson emphasize the importance of approaching a from both sides when considering limits?
-The lesson emphasizes that to find a limit, one must consider how the function values behave as x approaches a from both directions, ensuring the function's behavior is consistent.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Calculus (Version #2) - 1.1 Limits Graphically

Introduction to limits 2 | Limits | Precalculus | Khan Academy

Calculus Made EASY! Learning Calculus
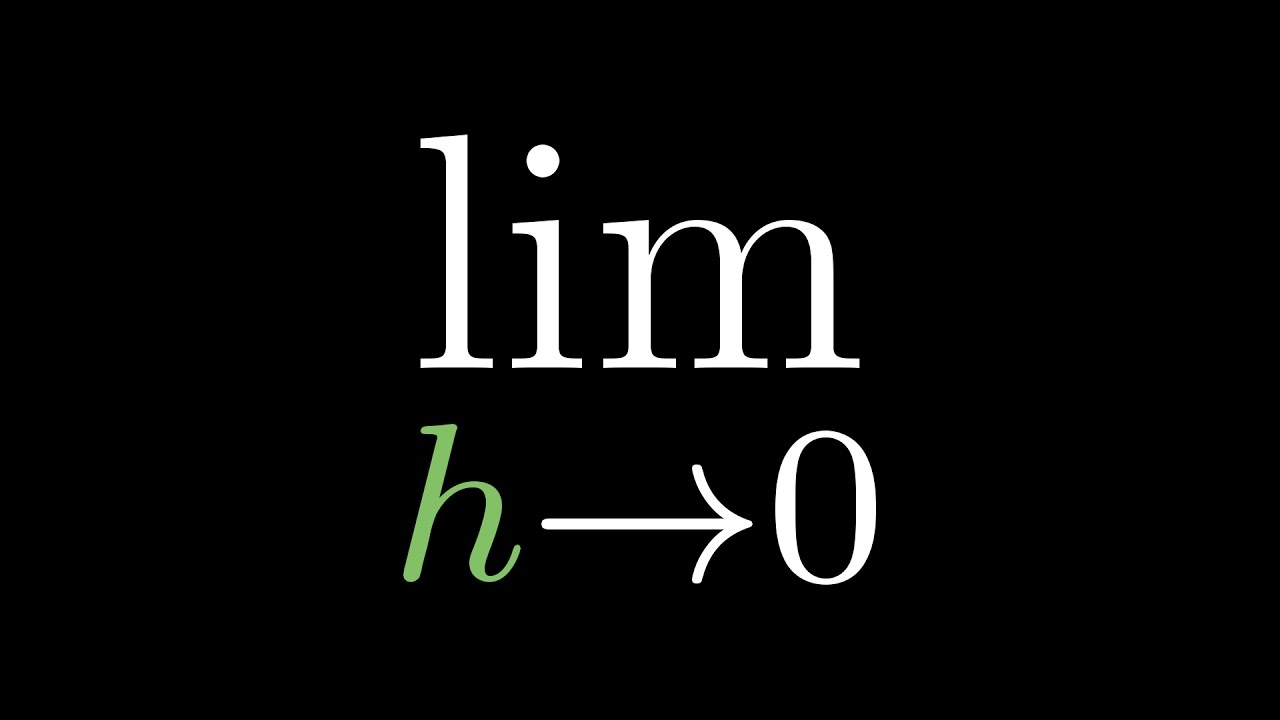
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

04. Limites e Continuidade. | Cálculo I.

Cálculo: Introdução e Noção Intuitiva de Limites (Aula 1 de 15)
5.0 / 5 (0 votes)
