The Fibonacci Sequence
Summary
TLDRThis presentation delves into the Fibonacci sequence, a series of numbers where each term is the sum of the two preceding ones, starting from 0 and 1. It highlights the sequence's historical origins with Fibonacci and its applications in nature, such as the arrangement of petals in flowers and the spiral patterns in plants and shells. The video also touches on the sequence's connection to the golden ratio and the golden spiral, illustrating how these mathematical concepts are reflected in the natural world.
Takeaways
- 🔢 The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, typically starting with 0 and 1.
- 🐰 It is famously illustrated by the problem of the growth of a population of ideal rabbits, where each month each pair of mature rabbits produces another pair.
- 🌼 The sequence is prevalent in nature, often observed in the arrangement of petals in flowers, the pattern of seeds in sunflowers, and the spirals of pinecones and pineapples.
- 🌀 The Fibonacci sequence is closely related to the golden ratio (φ), which is approximately 1.618 and is the limit of the ratios of successive Fibonacci numbers.
- 🎨 The golden spiral, a logarithmic spiral with a growth factor of φ, is approximated by the Fibonacci spiral, which is constructed by using quarter-circle arcs inscribed in squares of side lengths given by Fibonacci numbers.
- 🌿 The Fibonacci sequence and the golden ratio are not only mathematical concepts but also have aesthetic significance, often found in art, architecture, and design.
- 📚 The sequence was introduced to Western European mathematics by Leonardo Pisano, known as Fibonacci, in his 1202 book 'Liber Abaci', although it was known in Indian mathematics prior to this.
- 🔍 The Fibonacci sequence has applications in various fields including computer algorithms, mathematics, and even in the study of financial markets.
- 🌱 The number of spirals in many plants often corresponds to Fibonacci numbers, which can be observed in the arrangement of leaves on a stem or the pattern of seeds in a sunflower head.
- 🔄 The Fibonacci sequence demonstrates the interplay between mathematics and nature, highlighting the underlying mathematical patterns that govern natural growth and form.
Q & A
What is the Fibonacci sequence?
-The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1.
How is the Fibonacci sequence generated?
-The Fibonacci sequence is generated by starting with 0 and 1, and then each subsequent term is the sum of the two previous terms.
What is the recursive formula for the Fibonacci sequence?
-The recursive formula for the Fibonacci sequence is where a sub n equals a sub n minus 2 plus a sub n minus 1, with initial conditions a sub 0 equals 0 and a sub 1 equals 1.
Who is the Fibonacci sequence named after?
-The Fibonacci sequence is named after the Italian mathematician Leonardo Pisano of Pisa, also known as Fibonacci.
In what book did Fibonacci introduce the sequence?
-Fibonacci introduced the sequence in his 1202 book 'Liber Abaci'.
What is the rabbit problem associated with the Fibonacci sequence?
-The rabbit problem is a hypothetical scenario where a pair of newborn rabbits can reproduce after one month, and each month after that, they produce a new pair. The number of rabbit pairs grows according to the Fibonacci sequence.
Why is the Fibonacci sequence prevalent in nature?
-The Fibonacci sequence is prevalent in nature because it often reflects patterns of growth and arrangement found in plants, flowers, and even the spirals of galaxies and hurricanes.
What is the relationship between the Fibonacci sequence and the golden ratio?
-The golden ratio is the limit of the ratios of successive terms of the Fibonacci sequence. As the sequence progresses, the ratio of consecutive Fibonacci numbers approaches the golden ratio, which is approximately 1.618.
What is a Fibonacci spiral?
-A Fibonacci spiral is a spiral pattern created by drawing quarter-circle arcs in squares with Fibonacci-numbered side lengths, which approximates the golden spiral.
Where can Fibonacci spirals be observed in nature?
-Fibonacci spirals can be observed in nature in various forms such as the spirals of a pine cone, the arrangement of petals in a flower, or the growth pattern of plants like agaves.
What are some other interesting topics related to the Fibonacci sequence?
-Other interesting topics related to the Fibonacci sequence include its applications in art, architecture, computer algorithms, and its occurrence in various mathematical and scientific phenomena.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
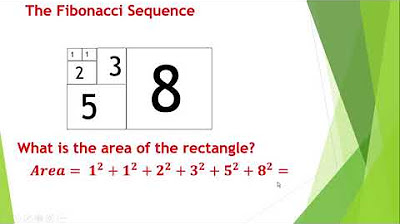
Fibonacci Sequence

What is the Fibonacci Sequence?

THE FIBONACCI SEQUENCE AND THE GOLDEN RATIO || MATHEMATICS IN THE MODERN WORLD

Unit 1 | Lesson 3: The Fibonacci Sequence (Mathematics in the Modern World)

On Fibonacci Sequence (GEC 104- Math in the Modern world)

Unit 1 Lesson 1 Practice Problems IM® Algebra 2TM authored by Illustrative Mathematics®
5.0 / 5 (0 votes)
