Why Calculus? - Lesson 1 | Infinity Learn NEET
Summary
TLDREl guion explora conceptos fundamentales del cálculo, como la velocidad instantánea y el área bajo curvas, a través de escenarios cotidianos como la caída de una pelota y el lanzamiento de una piedra. Desafía la lógica con el paradoxo de la dicotomía de Zenón y plantea la importancia del cálculo para resolver problemas de movimiento y áreas complejas, sugiriendo que el cálculo, con su enfoque en polígonos y aproximaciones, proporciona respuestas a estos misterios.
Takeaways
- 🏀 Nora juega con una pelota y se cuestiona sobre su movimiento.
- 📏 Nora suelta la pelota desde una altura de un metro y se pregunta sobre su velocidad a la mitad de su trayectoria.
- ⏱ La pelota tarda un segundo en llegar al punto medio, a 50 centímetros de altura.
- 🔢 Nora asume erróneamente que la velocidad de la pelota en el punto medio es de 50 centímetros por segundo, lo cual es la velocidad promedio.
- 🚀 La velocidad instantánea en el punto 'B' es diferente y se calcula con cálculo diferencial.
- 🤔 Nora se plantea por qué la pelota toca el suelo, considerando que si se divide la distancia en mitades infinitas, parece que tomaría un tiempo infinito.
- 🪄 Este razonamiento forma parte del paradoja de la dicotomía de Zenón, que también confundió a filósofos antiguos.
- 📐 La cálculo proporciona una respuesta satisfactoria a la paradoja de Zenón y a otros problemas similares.
- 🌊 Al lanzar una piedra, la cálculo ayuda a determinar el ángulo óptimo para alcanzar la mayor distancia.
- 📉 El cálculo también es fundamental para encontrar áreas bajo curvas, algo que no se puede hacer con formas geométricas simples.
- 📐 La idea central del cálculo se utiliza desde la antigüedad para aproximar áreas, como la del círculo, mediante el método de los polígonos inscritos y circumscriptos.
Q & A
¿Qué hace Nora mientras juega con una pelota?
-Nora se muestra curiosa acerca del movimiento de la pelota y la suelta en el suelo para observar su caída.
¿Cuál es la pregunta que se hace Nora sobre la pelota al llegar a la mitad de su trayectoria?
-Nora se pregunta cuál será la velocidad de la pelota al alcanzar la mitad de su trayectoria.
¿De qué altura inicia la caída de la pelota Nora?
-Nora suelta la pelota desde una altura de un metro sobre el suelo.
¿Cuál es la conclusión incorrecta que Nora llega a respecto a la velocidad de la pelota en el punto B?
-Nora incorrectamente concluye que la velocidad de la pelota en el punto B es de 50 centímetros por segundo, lo cual es en realidad la velocidad promedio hasta ese punto.
¿Por qué la velocidad que Nora calcula no es la velocidad instantánea en el punto B?
-La velocidad que Nora calcula no es instantánea porque asume una velocidad constante, pero en realidad la velocidad de la pelota aumenta a medida que cae.
¿Qué rama de las matemáticas ayuda a calcular la velocidad instantánea de un objeto?
-El cálculo, una rama de las matemáticas, ayuda a calcular la velocidad instantánea de un objeto.
¿Qué paradoja plantea Nora sobre por qué la pelota nunca debería tocar el suelo?
-Nora plantea la paradoja de la dicotomía de Zenón, que sugiere que la pelota nunca debería tocar el suelo debido a la división infinita de la distancia que debe recorrer.
¿Cómo podría calcularse la velocidad instantánea de un objeto utilizando el cálculo?
-La velocidad instantánea se puede calcular tomando el límite de la velocidad promedio cuando el intervalo de tiempo tiende a cero, lo cual es un concepto fundamental del cálculo.
¿En qué otro ejemplo del guion se menciona el uso del cálculo para resolver un problema real?
-Se menciona el uso del cálculo para determinar el ángulo óptimo para lanzar una piedra y cubrir la mayor distancia posible.
¿Cómo se relaciona el cálculo con la determinación del área bajo una curva?
-El cálculo permite integrar funciones para encontrar áreas bajo curvas, algo que no es posible utilizando solo formas geométricas simples.
¿Qué método utilizado por los matemáticos griegos para encontrar el área de un círculo se menciona en el guion?
-Se menciona el método de la exhaustión, que consistía en inscribir y circumscribir polígonos en el círculo para aproximar su área.
¿Cuál es la idea central del cálculo que se utiliza para resolver los problemas mencionados en el guion?
-La idea central del cálculo es la aproximación de áreas y longitudes utilizando polígonos con un número cada vez mayor de lados, lo que se relaciona con los límites y derivadas del cálculo.
¿Qué invita el guion a hacer en la sección de comentarios?
-El guion invita a los lectores a compartir sus pensamientos en la sección de comentarios sobre la paradoja planteada y cómo abordar el problema de la velocidad instantánea.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Cálculo: Que es el Cálculo, intuitivamente ...

2.8.a) Razones de Cambio en Ciencias Naturales y Sociales. Definición y ejemplo

Física 1 Caída Libre y Tiro Vertical

Curso de cinemática Amautas: 3. El movimiento

Pensamiento matemático 3. Progresión 2a. Origenes del calculo.
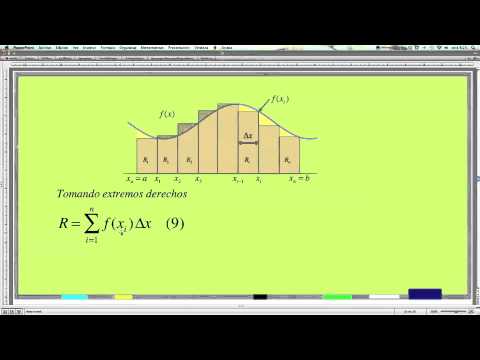
Calculo Integral 04: La integral definida. The definite integral.
5.0 / 5 (0 votes)
