Two particles of masses m_1 and m_2 are tied to the ends of an elastic string of natural length a..
Summary
TLDRThe video script discusses the concept of elastic motion, specifically harmonic motion, using a physics-based approach. It explains the natural frequency of oscillation and how it relates to the mass and tension of a system. The script also covers the mathematical representation of this motion, including the equations of motion and the concept of period. It aims to provide clarity on the problem-solving process in physics, particularly in understanding the behavior of oscillating systems.
Takeaways
- 📚 The script discusses the concept of elastic properties and their mathematical representation, possibly in the context of physics.
- 🎵 There are mentions of 'music' which could be related to the harmonic nature of the motion being discussed.
- 🔍 The term 'elas-tic' is repeated, indicating a focus on elasticity and its role in the subject matter.
- 📏 A distinction is made between natural length and the stretched or compressed length of an elastic material.
- 📉 The script describes a method to project the displacement of an elastic object directly after the loss of tension.
- 📚 There's an equation involving 'm1' and 'm2', which could represent the masses in a physical system.
- 🔗 The relationship between the acceleration of 'm2' and the force applied is discussed, with reference to Newton's second law of motion.
- 🔄 The motion of 'm2' is described as simple harmonic motion, a common topic in physics dealing with oscillatory movements.
- 📐 The script mentions the calculation of displacement over time, which is integral to understanding motion.
- 🔢 The importance of the period of motion is highlighted, indicating a discussion on periodic phenomena in physics.
- 📉 The script seems to involve solving for variables in a physics problem, possibly related to the motion of a system under force.
Q & A
What is the physical setup described in the script?
-The setup involves two masses, m1 and m2, tied to the ends of an elastic string of natural length 'a'. The system is placed on a smooth table, and m2 is projected with a velocity directly away from m1.
What is meant by 'natural length' of the elastic string?
-The 'natural length' of the elastic string refers to its length when it is neither stretched nor compressed, meaning no external force is acting on it to change its length.
What kind of motion does mass m2 undergo after being projected?
-After being projected, mass m2 undergoes simple harmonic motion (SHM) relative to mass m1.
How is the extension in the elastic string represented in the problem?
-The extension in the elastic string at any time is represented by 'x', which is the difference between the distance 'L' and the natural length 'a' of the string.
What is the significance of the smooth table in the problem setup?
-The smooth table implies that there is no friction between the masses and the table, allowing the motion of the masses to be analyzed without the influence of frictional forces.
How is the force acting on mass m1 described in the script?
-The force acting on mass m1 is described as a function of the elastic force in the string, which is proportional to the extension 'x' of the string from its natural length.
What role does the constant 'a' play in the equations of motion?
-The constant 'a' represents the natural length of the elastic string and is used in the equations to determine the extension and the resulting force acting on the masses.
How is the time period of the simple harmonic motion derived?
-The time period of the simple harmonic motion is derived using the formula for SHM, incorporating the masses m1 and m2 and the properties of the elastic string.
What is the relation between the acceleration of mass m2 and the extension of the string?
-The acceleration of mass m2 is directly related to the extension of the string, as the restoring force that causes SHM is proportional to this extension.
What is the final result or conclusion of the problem discussed in the script?
-The final result is that the motion of mass m2 is simple harmonic, with a periodic time dependent on the masses m1 and m2 and the properties of the elastic string.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
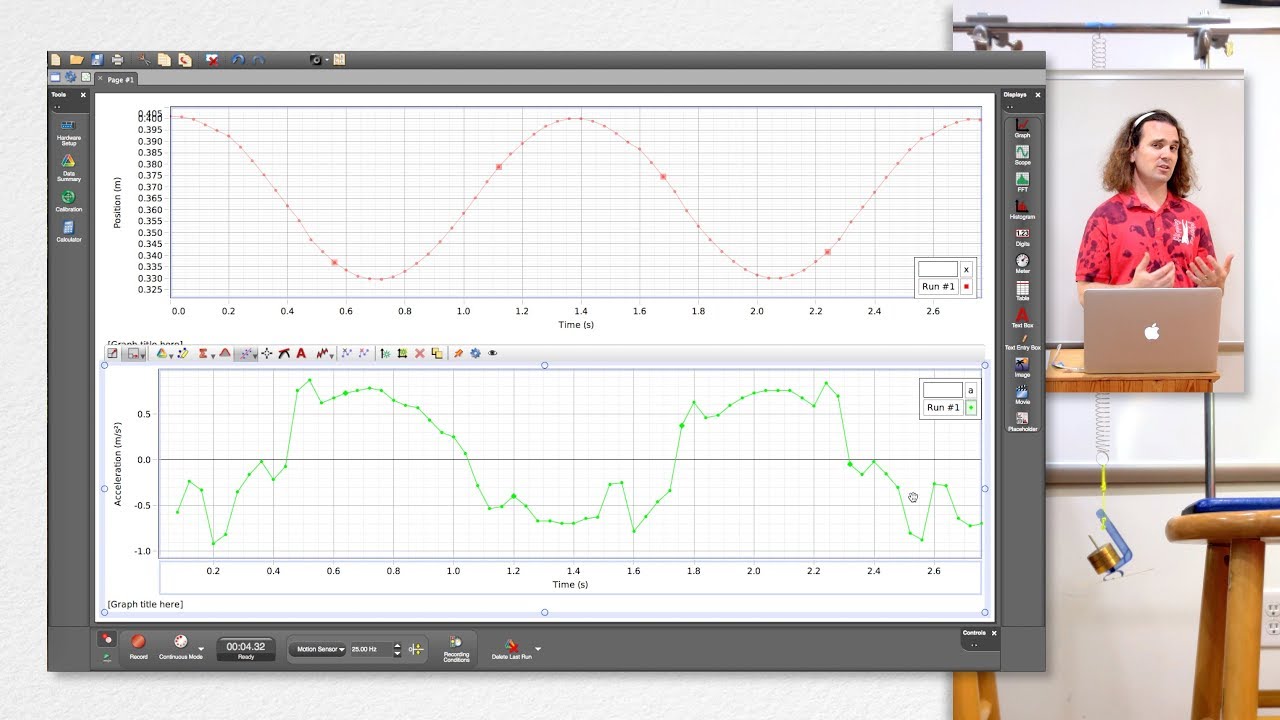
Demonstrating Position, Velocity, and Acceleration of a Mass-Spring System
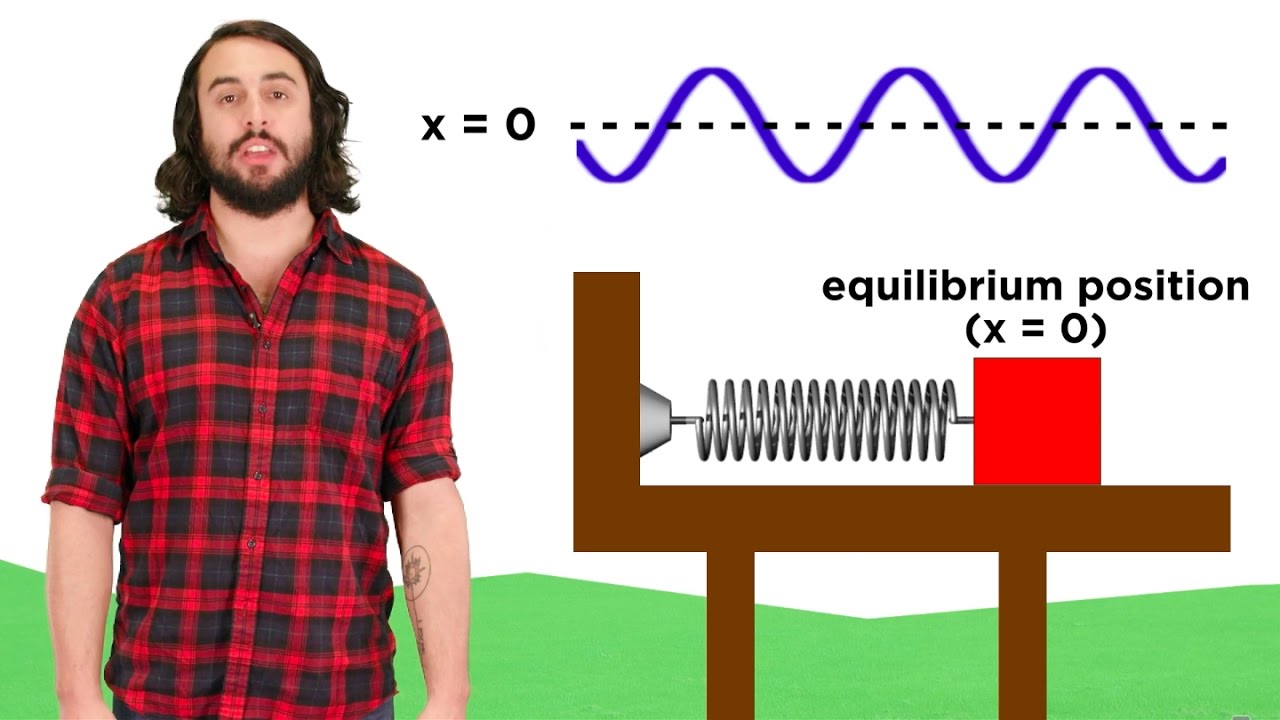
Simple Harmonic Motion: Hooke's Law

Dạng 1 Vận tốc của vật dao động điều hòa

Pengantar Materi Getaran dan Gelombang pada Mata Kuliah Fisika Dasar ITK 2020/2021

Drgania, ruch drgający #1 [ Ruch drgający i fale ]

Ayunan sederhana yang digantungkan pada langit-langit lift yang diam memiliki periode ayunan T.
5.0 / 5 (0 votes)
