Normal Distribution: Calculating Probabilities/Areas (z-table)
Summary
TLDRThis video tutorial demonstrates how to use standard normal distribution tables to calculate probabilities. It explains the concept of a z-score, which measures how many standard deviations a data point is from the mean. The script guides through examples of finding probabilities for scores below a certain value, above another, and between two values. It concludes with the method to determine 'less than', 'greater than', and 'between' areas using cumulative tables, emphasizing the importance of subtracting areas, not z-values, for the latter.
Takeaways
- 📚 The video explains how to use standard normal distribution tables to calculate probabilities.
- 📉 A normal distribution is symmetric and bell-shaped, with the total area under the curve equaling 1 or 100%.
- 📍 The standard normal distribution has a mean (µ) of 0 and a standard deviation (σ) of 1.
- 🔄 The formula to convert any score x from a normal distribution to a standard normal score (z-score) is z = (x - µ) / σ.
- 📊 The z-score represents how many standard deviations a score is from the mean.
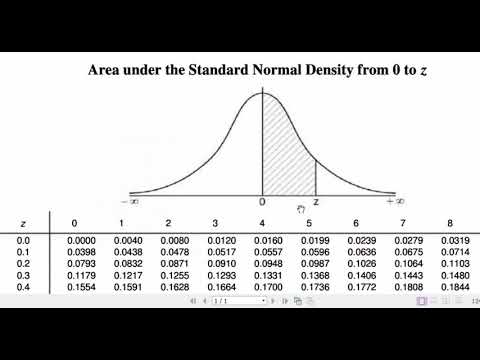
- 🔑 The video uses 'Less Than' cumulative tables for standard normal distribution, which are typically shaded for the left tail.
- 🔍 For a given exam score example, the z-score for x = 54 is calculated as -1.22 (rounded from -1.2222).
- 📌 The probability that a score is less than 54 is found by looking up the area to the left of z = -1.22 in the table, which is 0.1112 or 11.12%.
- 🚫 In continuous distributions like the normal distribution, 'at least' and 'greater than' are treated the same for probability calculations.
- 🔢 For the exam example, the probability that a score is at least 80 is calculated by subtracting the area to the left of z = 1.67 from 1, resulting in 0.0475 or 4.75%.
- 🌐 To find the probability of a score being between two values, subtract the area to the left of the smaller z-score from the area to the left of the larger z-score, as demonstrated with the range between 70 and 86.
Q & A
What is a normal distribution?
-A normal distribution is a symmetric, bell-shaped distribution where the area under the curve is 1 or 100%, representing the probability of all possible outcomes.
What distinguishes a standard normal distribution from other normal distributions?
-A standard normal distribution, also known as the z-distribution, has a mean (µ) of 0 and a standard deviation (σ) of 1, making it a special case of the normal distribution.
What is the formula to convert a score from any normal distribution to a standard normal score?
-The formula to convert a score x from any normal distribution to a standard normal score, also known as the z-score, is z = (x - µ) / σ.
What are the 'Less Than' cumulative tables used for in the context of standard normal distribution?
-The 'Less Than' cumulative tables are used to find the probability of a score being less than a certain value in a standard normal distribution by looking up the corresponding z-score.
How do you calculate the z-score for a score of 54 given a mean of 65 and a standard deviation of 9?
-To calculate the z-score for a score of 54, you subtract the mean (65) from the score (54) and then divide by the standard deviation (9), which results in a z-score of -1.2222, rounded to -1.22 for table lookup.
What is the probability that a score is less than 54 given the same distribution as in the example?
-The probability that a score is less than 54 is found by looking up the corresponding z-score of -1.22 in the standard normal table, which gives an area of 0.1112 or 11.12%.
How does the concept of 'at least' relate to 'greater than' in continuous distributions like the normal distribution?
-In continuous distributions, such as the normal distribution, 'at least' and 'greater than' are treated the same because the probability of a score being exactly at a certain value is zero.
What is the probability that a score is at least 80 given the exam scores distribution in the example?
-The probability that a score is at least 80 is found by looking up the z-score of 1.67 in the standard normal table, which gives an area of 0.9525. Subtracting this from 1 gives 0.0475 or 4.75%.
How do you calculate the probability of a score falling between two values, such as 70 and 86, in the given distribution?
-To find the probability of a score falling between 70 and 86, calculate the z-scores for both values, look up the corresponding areas in the standard normal table, and subtract the smaller area from the larger one, resulting in 0.2778 or 27.78%.
What is the key takeaway when using the standard normal table to find areas for 'less than,' 'greater than,' and 'between' scenarios?
-When using the standard normal table, for 'less than' scenarios, the area in the table is the answer. For 'greater than,' subtract the table area from 1. For 'between' scenarios, subtract the smaller area (corresponding to the smaller z-value) from the larger area (corresponding to the larger z-value).
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Finding Areas Using the Standard Normal Table (for tables that give the area between 0 and z)
Peluang Distribusi NORMAL beserta Contoh Soal Pembahasan

Math 220 Sec 8 5 Part 1
Distribusi Probabilitas Normal

Z-Scores, Standardization, and the Standard Normal Distribution (5.3)

The Normal Distribution and Shoplifting (DeSTRESS Film 12)
5.0 / 5 (0 votes)
