1 Funcion lineal
Summary
TLDREl guión ofrece una introducción a las funciones lineales, explicando su definición y características fundamentales. Define la función lineal como 'f(x) = mx + b', donde 'm' es la pendiente y 'b' es el punto de intersección en el eje y. Se discute cómo calcular la pendiente a partir de dos puntos y cómo determinar si la función es creciente, decreciente o constante. Se ejemplifica con una ecuación de recta para encontrar 'm' y 'b', y se asocia con una función lineal, demostrando el proceso de despeje para identificar los valores correctos de 'm' y 'b'.
Takeaways
- 📚 La función lineal se define como f(x) = mx + b, donde m y b son constantes reales que representan la pendiente y el punto de intersección con el eje y, respectivamente.
- 📈 La pendiente m indica si la función es creciente, decreciente o constante, y su valor nos da información sobre el grado de inclinación de la recta.
- 📍 El valor de b nos dice en qué punto la recta interseca el eje y.
- 🔍 Para calcular la pendiente a partir de dos puntos de la función lineal, se utiliza la fórmula (y2 - y1) / (x2 - x1).
- 📐 La recta asociada a la función lineal tiene la forma y = mx + b, y se puede despejar para encontrar el valor de b.
- 🤔 Al encontrar la intersección con el eje x, se utiliza la fórmula m * 0 + b, lo que nos da el valor de b.
- 🔢 Para determinar el punto de intersección con el eje y, se utiliza la fórmula 0 = mx + b, lo que nos permite encontrar el valor de b.
- 📉 La monotonía de la función (si es creciente, decreciente o constante) se deduce del signo de m.
- 👉 Al resolver ejercicios con rectas, es fundamental asegurarse de que la ecuación esté en la forma y = mx + b para identificar correctamente a m y b.
- 📝 En el ejemplo proporcionado, se muestra cómo despejar una ecuación de recta para encontrar los valores de m y b y, a partir de ellos, la función lineal asociada.
Q & A
¿Qué es una función lineal y cómo se define?
-Una función lineal es una relación matemática que se describe por una recta en el plano cartesiano. Se define como f(x) = mx + b, donde m es la pendiente de la recta y b es el ordenada al origen, ambos son constantes reales.
¿Qué información proporciona la pendiente 'm' de una función lineal?
-La pendiente 'm' indica cuánto varía la función lineal en el eje y por unidad en el eje x. También nos dice si la función es creciente (m > 0), decreciente (m < 0) o constante (m = 0), y el grado de inclinación de la recta con respecto al eje de las abscisas.
¿Cómo se calcula la pendiente 'm' de una función lineal a partir de dos puntos?
-Para calcular la pendiente 'm' a partir de dos puntos (x1, y1) y (x2, y2), se utiliza la fórmula m = (y2 - y1) / (x2 - x1).
¿Cómo se determina el valor de 'b' en una función lineal dada dos puntos y la pendiente?
-Para determinar el valor de 'b', se puede utilizar cualquiera de los dos puntos y la pendiente 'm' en la fórmula b = y - mx, donde (x, y) son las coordenadas del punto dado.
¿Qué significa el valor de 'b' en la función lineal f(x) = mx + b?
-El valor de 'b' representa el punto en el que la recta de la función lineal interseca el eje y, es decir, el valor de la función cuando x = 0.
¿Cómo se determina si una función lineal intersecta el eje x?
-Para determinar si una función lineal intersecta el eje x, se calcula el valor de x cuando y = 0, utilizando la fórmula x = -b/m.
¿Cómo se determina el punto de intersección de una función lineal con el eje y?
-El punto de intersección de una función lineal con el eje y se determina cuando x = 0, lo cual se calcula sustituyendo x = 0 en la función, obteniendo y = b.
¿Qué pasos se deben seguir para determinar m y b si se tiene una ecuación de recta en forma no estándar?
-Primero, se debe expresar la ecuación en la forma estándar y = mx + b. Luego, se despeja y para aislarla, y finalmente se identifican los valores de m y b a partir de la ecuación despejada.
¿Cómo se asocia una recta dada con una función lineal?
-Una recta dada se asocia con una función lineal expresando la recta en la forma f(x) = mx + b, donde m es la pendiente y b es el ordenada al origen.
En el ejemplo dado en el guion, ¿cómo se determinan los valores de m y b para la recta 5y - 25x + 30 = 0?
-Se despeja la y de la ecuación 5y - 25x + 30 = 0 obteniendo y = 5x - 6. Luego, se identifican que m = 5 (la pendiente) y b = -6 (el ordenada al origen).
¿Qué función lineal se asocia con la recta dada en el ejemplo del guion?
-La función lineal asociada con la recta 5y - 25x + 30 = 0, una vez despejada y expresada en forma estándar, es f(x) = 5x - 6.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
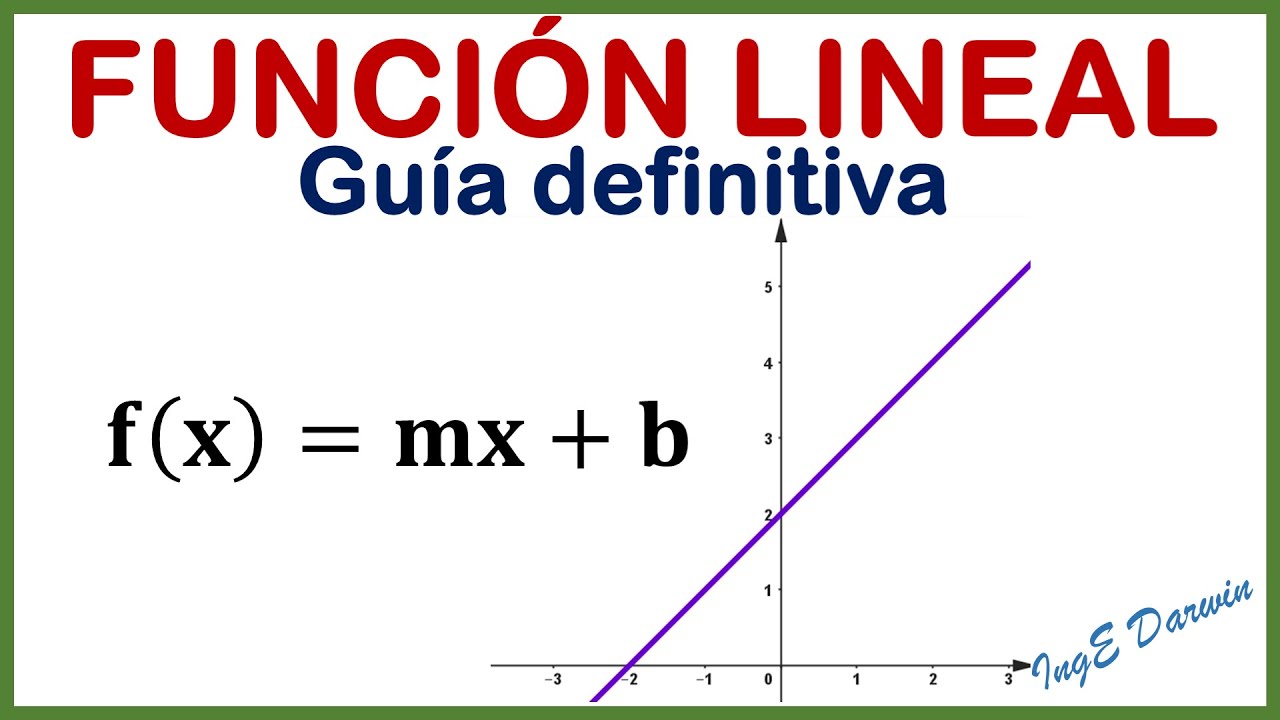
Función Lineal: introducción, características, gráfica, todo lo que necesitas saber | Clase 1

Precálculo, función, dominio y rango

Tipos de funciones
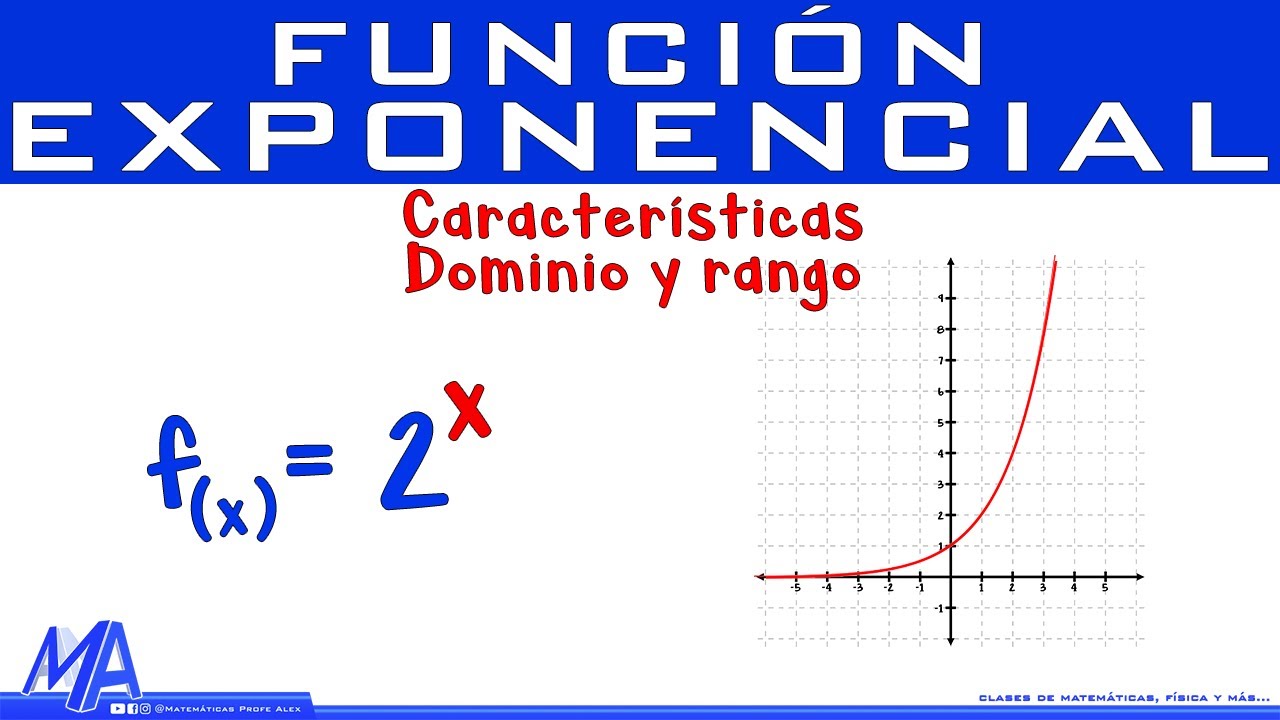
Función Exponencial | Características

Sistema muscular: Tipos, Clasificación, Músculos principales - Anatomía Humana | Kenhub

Polímeros de adición y condensación | Equipo 4.
5.0 / 5 (0 votes)
