Función Lineal: introducción, características, gráfica, todo lo que necesitas saber | Clase 1

Summary

Este video ofrece una introducción a las funciones lineales, explicando su definición y características. Se exploran las distintas formas de representar una función lineal, incluyendo su representación algebraica (fx = mx + b) y gráfica (una línea recta en el plano cartesiano). Identifica los elementos clave como la pendiente (m) y el término independiente (b), y cómo estos afectan la gráfica. Se realizan actividades para modificar la pendiente y el término independiente, y se explica cómo identificar estos elementos es crucial para analizar el comportamiento de las funciones lineales. Finalmente, se aborda la creación de un bosquejo de la gráfica a partir de la pendiente y el término independiente, y se invita a los estudiantes a participar en futuras clases para un estudio más profundo.

Takeaways

• 😀 La función lineal es una función polinómica de grado 1, representada algebraicamente como \( y = mx + b \).
• 📈 La representación gráfica de una función lineal es una línea recta en el plano cartesiano, que puede ser creciente o decreciente.
• 📊 Se puede representar una función lineal mediante tabla de valores, conocida como registro tabular, y también mediante representación dinámica utilizando software como Geogebra.
• 🔢 Los elementos clave de una función lineal son la variable \( y \), la variable independiente \( x \), la pendiente \( m \) y el término independiente \( b \).
• ↗️ La pendiente \( m \) indica la inclinación de la línea recta con respecto al eje de las abscisas; si es positiva, la función es creciente.
• ↘️ Si la pendiente \( m \) es negativa, la función lineal es decreciente, mostrando una disminución a medida que aumenta \( x \).
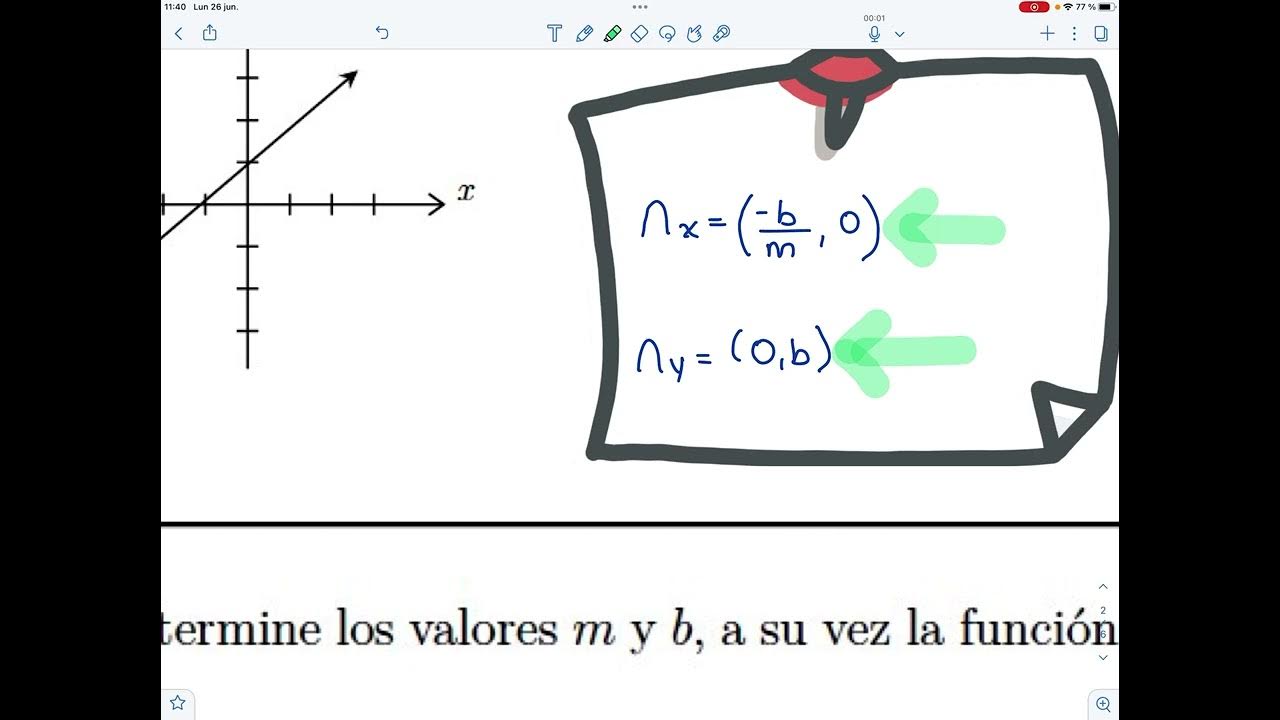
• 🔴 El término independiente \( b \) representa el punto de intersección de la línea recta con el eje de las ordenadas (eje \( y \)) y se conoce como ordenada al origen.
• 📐 Para graficar una función lineal, se puede realizar un bosquejo aproximado conociendo la pendiente y el término independiente, lo cual ayuda a entender el comportamiento de la función.
• 🔄 La monotonía de una función lineal, que es su comportamiento constante, creciente o decreciente, se analiza de izquierda a derecha en el plano cartesiano.
• 💬 En caso de dudas o consultas sobre las funciones lineales, se recomienda dejar un comentario para obtener asistencia adicional.

Q & A

¿Qué es una función lineal?

Una función lineal es una función polinómica de grado 1, cuya representación algebraica es de la forma f(x) = mx + b, donde m es la pendiente y b es el término independiente.

¿Cómo se representa gráficamente una función lineal?

La representación gráfica de una función lineal es una línea recta en el plano cartesiano, que puede ser creciente o decreciente dependiendo de la pendiente.

¿Qué elementos identifica la función lineal y cómo se representan algebraicamente?

Los elementos de la función lineal son la variable y (o FX), la variable independiente x, la pendiente (m) y el término independiente (b). Algebraicamente, se representa como y = mx + b.

¿Cómo se identifican la pendiente y el término independiente en una función lineal dada?

La pendiente se identifica como el coeficiente que acompaña a la variable x, mientras que el término independiente es el número que aparece por sí solo en la función, generalmente anteponiendo el signo más o menos.

¿Qué significa el término 'variable independiente' en el contexto de una función lineal?

La variable independiente es la variable x en una función lineal, que tiene un exponente de 1, indicando que la función es de primer grado.

¿Cuál es la diferencia entre una función lineal creciente y una decreciente?

Una función lineal creciente tiene una pendiente positiva, lo que significa que la gráfica se inclina hacia arriba. Por otro lado, una función lineal decreciente tiene una pendiente negativa, lo que significa que la gráfica se inclina hacia abajo.

¿Qué representa el término independiente b en la función lineal y cómo se identifica en la gráfica?

El término independiente b representa el punto de intersección de la función lineal con el eje y. En la gráfica, se identifica como el valor en el eje y donde la línea recta corta este eje.

Si una función lineal no muestra la variable x, ¿qué tipo de función es y cómo se representa gráficamente?

Si una función lineal no muestra la variable x, se trata de una función constante, que se representa gráficamente como una recta horizontal que corta el eje y en el valor del término independiente b.

¿Cómo se realiza un bosquejo aproximado de la gráfica de una función lineal sin una tabla de valores?

Para realizar un bosquejo aproximado de la gráfica de una función lineal sin una tabla de valores, se identifican la pendiente y el término independiente, y se analiza la monotonía (creciente, decreciente o constante) y el punto de corte con el eje y.

¿Qué es la monotonía en una función lineal y cómo se determina?

La monotonía en una función lineal se refiere a si la función es creciente, decreciente o constante, lo que se determina por el signo de la pendiente. Se analiza de izquierda a derecha en la gráfica.

Outlines

00:00

📚 Introducción a la función lineal

El primer párrafo introduce el tema de la función lineal, explicando que es una función polinómica de primer grado. Se menciona la representación algebraica (y = mx + b) y gráfica (una línea recta en el plano cartesiano). Además, se habla de la representación tabular y dinámica. Se enfatiza la importancia de identificar elementos como la pendiente (m) y el término independiente (b) para analizar el comportamiento de la función. Se describen actividades para modificar estos elementos y se ejemplifica con funciones dadas.

05:01

🔍 Identificación de elementos en funciones lineales

Este párrafo se enfoca en la identificación de la pendiente y el término independiente en funciones lineales. Se recomienda un orden específico para identificar estos elementos y se explica que la ausencia de la variable x en la función indica una función constante. Se discuten los tres posibles comportamientos de la gráfica en función de la pendiente: creciente, constante o decreciente. Se resume que la pendiente positiva indica una gráfica creciente, la pendiente cero una gráfica constante y la pendiente negativa una gráfica decreciente. Se introduce el término independiente como el punto de intersección con el eje y.

10:05

📈 Análisis gráfico de funciones lineales

El tercer párrafo profundiza en el análisis gráfico de las funciones lineales basado en la pendiente y el término independiente. Se describe cómo determinar si la gráfica es creciente o decreciente y cómo ubicar el punto de intersección con el eje y. Se ejemplifican funciones con pendientes positivas, negativas y cero, y se muestra cómo se grafican respectivamente. Se destaca que la ausencia del término independiente implica que la gráfica pasa por el origen, y se concluye con una función constante que corta el eje y en -1, proporcionando un bosquejo preciso de la gráfica.

Keywords

💡Función lineal

Una función lineal es una relación entre dos variables donde la salida es una línea recta cuando se grafica. En el guion, se define como una función polinómica de grado 1, representada algebraicamente como \( y = mx + b \), donde \( m \) es la pendiente y \( b \) es el término independiente. Este concepto es fundamental para entender cómo varía una cantidad con respecto a otra en una relación lineal directa y proporcional.

💡Pendiente

La pendiente, representada por la letra \( m \) en la ecuación de una función lineal, indica la inclinación de la línea en el plano cartesiano. En el guion, se explica que la pendiente determina si la función es creciente, decreciente o constante, dependiendo de si su valor es positivo, negativo o cero, respectivamente. Esto es crucial para entender el comportamiento de la función a lo largo de su gráfico.

💡Término independiente

El término independiente, representado por la letra \( b \) en la ecuación de la función lineal, es el punto en el que la línea intersecta el eje de las ordenadas (eje y). Según el guion, si \( b \) es positivo, la línea intersecta el eje y en un punto por encima del origen; si es cero, la línea pasa por el origen; y si es negativo, intersecta el eje y en un punto por debajo del origen.

💡Monotonía

La monotonía de una función lineal se refiere a si la función es creciente, decreciente o constante a lo largo de su dominio. En el guion, se menciona que la monotonía se analiza de izquierda a derecha en el gráfico y se relaciona con el signo de la pendiente: creciente si la pendiente es positiva, decreciente si es negativa y constante si la pendiente es cero.

💡Gráfica creciente

Una gráfica creciente es aquella en la que la función aumenta a medida que avanzamos de izquierda a derecha. En el guion, se ilustra con una recta que se desplaza hacia arriba en el plano cartesiano, lo cual ocurre cuando la pendiente de la función lineal es positiva.

💡Gráfica decreciente

Una gráfica decreciente es aquella donde la función disminuye a medida que avanzamos de izquierda a derecha. El guion describe este comportamiento como una recta que se inclina hacia abajo en el plano cartesiano, lo que sucede cuando la pendiente de la función lineal es negativa.

💡Gráfica constante

Una gráfica constante es aquella donde la función mantiene el mismo valor a lo largo de toda su extensión. En el guion, se muestra que esto se representa gráficamente como una línea horizontal, lo cual ocurre cuando la pendiente de la función lineal es cero.

💡Eje de las abscisas

El eje de las abscisas, también conocido como eje x, es uno de los ejes en el plano cartesiano. En el guion, se menciona que es el eje horizontal y se refiere a la variable independiente en una función lineal, que se manipula para observar cómo afecta a la variable dependiente.

💡Eje de las ordenadas

El eje de las ordenadas, también conocido como eje y, es el otro eje en el plano cartesiano. Según el guion, es el eje vertical y representa la variable dependiente en una función lineal, que es la cantidad que cambia en respuesta a cambios en la variable independiente.

💡Tabla de valores

Una tabla de valores es una herramienta utilizada para graficar funciones, donde se listan los valores de la variable independiente y sus correspondientes valores dependientes. Aunque no se detalla en el guion, es una técnica que se utiliza para determinar los puntos que se van a graficar en el plano cartesiano antes de trazar la línea.

Highlights

Definición de una función lineal como una función polinómica de grado 1.

Representación algebraica de una función lineal: f(x) = mx + b.

Representación gráfica de una función lineal como una línea recta en el plano cartesiano.

Introducción a la representación de funciones lineales mediante tabla de valores (registro tabular).

Identificación de variables en una función lineal: y (o f(x)) y x como variable independiente.

Importancia de la pendiente (m) en la función lineal como medida de inclinación respecto al eje x.

El término independiente (b) como punto de intersección de la función con el eje y.

Actividad para identificar elementos de la función lineal: pendiente y término independiente.

Ejemplo práctico: Identificación de la pendiente y término independiente en f(x) = 3x + 1.

Ejemplo de función lineal con pendiente negativa: f(x) = -2x.

Función lineal sin término independiente: f(x) = 4 + 7x.

Función constante como una especialización de la función lineal con pendiente cero.

Importancia de la monotonía en la gráfica de funciones lineales: creciente, decreciente o constante.

Análisis del término independiente y su influencia en el punto de corte con el eje y.

Actividad de bosquejo de gráficas de funciones lineales basadas en la pendiente y término independiente.

Representación gráfica de una función lineal creciente con término independiente positivo.

Representación gráfica de una función lineal decreciente con término independiente positivo.

Caso especial: Función lineal que pasa por el origen de coordenadas (término independiente cero).

Función constante y su representación gráfica como una línea horizontal.

Conclusión de la clase y anticipación de futuras clases sobre funciones lineales.

Transcripts

Qué tal amigazos cómo están Espero que

se encuentren súper bien hoy vamos a

estudiar la función lineal y primero

veremos una pequeña introducción donde

hablaremos de la definición y

características luego conoceremos las

distintas formas de representar una

función lineal continuaremos

identificando los elementos como son las

variables la pendiente y el término

independiente y en cada uno de estos

apartados realizaremos actividades de

tal manera que los conceptos queden

claros Así que la clase va a estar muy

interesante comenzamos bien una función

lineal es una función polinómica de

grado 1 cuya representación algebraica

es la siguiente FX es igual a MX + B

Aunque en lugar de FX también podemos

Ubicar la variable Y entonces nos queda

y igual a MX más B ahora la

representación gráfica de una función

lineal es una línea recta que se grafica

en el plano cartes de hecho todas las

funciones se grafican en el famoso plano

cartesiano que está compuesto por dos

ejes el eje de las abscisas o x y el eje

de las ordenadas o Y entonces como ya se

mencionó la Gráfica de esta función es

una línea recta que puede ser creciente

o decreciente en este momento estamos

ubicando una gráfica creciente así que

hasta el momento hemos visto la

definición la representación algebraica

y la representación gráfica Sin embargo

a una función lineal también la podemos

representar mediante tabla de valores y

a esto lo conocemos como el registro

tabular Y si nosotros utilizamos algún

software o programa como geogebra para

graficar las funciones estamos

utilizando las representación dinámica y

Qué les parece si en este momento

conocemos como identificar los elementos

de la función lineal Entonces por un

lado tenemos las variables empezando con

FX o y que ya quedamos que es lo mismo

que corresponde a la variable de en

cambio x es la variable independiente y

aquí hay que mencionar algo importante

esta función es de grado 1 lo que

significa que la variable X La variable

independiente tiene exponente 1

recordemos que el exponente 1 no se

escribe pero por esta razón la función

es de grado 1 o primer grado continuando

con los elementos tenemos la famosa

pendiente que es del grado de

inclinación respecto al eje de las

abscisas y finalizamos con b el término

independiente que es el punto de

intersección con el eje de las ordenadas

es decir con el eje Y entonces conocer

estos elementos y sobre todo saberlos

identificar es demasiado importante

porque nos servirá para analizar el

comportamiento de la función lineal y

bueno Más adelante veremos a detalle que

representa cada uno de los elementos

porque en este momento vamos a realizar

la primera actividad que les parece esta

actividad consiste en Modificar el valor

de la pendiente y el término

independiente y partimos recordando la

representación o registro algebraico de

la función lineal fdx igual a MX + B

vamos con el primer ejercicio FX es

igual a 3x + 1 miren acá la pendiente es

del número que Acompaña a la variable X

en cambio el término independiente Por

así decirlo es el número que se

encuentra solo si nosotros observamos

esta función nos damos cuenta que la

constante o número que acompaña la

variable x es 3 lo que significa que en

este caso la pendiente equivale a 3

escribimos muy bien y bueno el término

independiente es 1 B es igual a 1 muy

sencillo no Simplemente recordemos que

la pendiente acompaña x y el término

independiente el número que está solo

sigamos con la siguiente función y es

igual a 4x menos 5 la pendiente es 4

porque acompaña la variable copiamos 4 m

igual a 4 y el término independiente en

esta ocasión es -5 el número que se

encuentra solito por acá tenemos la

función y de X que al final viene a ser

lo mismo que y de X es igual a -2x está

claro que la pendiente en este caso es

-2 porque -2 multiplica a x escribimos

menos 2 Pero qué sucede no aparece el

término independiente cuando eso pasa

significa que acá Este término está

sumando a 0 porque el 0 no nos suma ni

nos resta entonces concluimos que B es

igual a cero el término independiente en

esta función es cero por favor nunca lo

olviden cuando no se visualiza el valor

de B significa que equivale a 0 veamos

Qué sucede con esta función y es igual a

4 + 7x cuidado con pensar que la

pendiente el 4 y el término

independiente es 7 No eso es incorrecto

escuchen muchachos cuando estamos

iniciando con este tema de

identificación de los elementos de la

función lineal se recomienda ordenar los

elementos y lo haremos por acá para que

ustedes puedan comprender entonces

copiamos la variable y igual y primero

debe escribirse la pendiente acompañado

de la variable x es decir 7x luego viene

el término independiente que para este

caso es 4 positivo Y acá es mucho más

sencillo identificar el valor de la

pendiente Cuánto es pues 7 y el término

independiente equivale a 4 Claro está

que cuando ustedes ya tengan práctica

tal cual está escrita la función y ya

pueden identificar los elementos de una

manera sencilla pero por el momento

vamos paso a paso y qué sucede con esta

función ustedes dirán pero profe no

aparece la variable x Bueno a se le

conoce como una función constante y de

seguro ustedes van a tener la

interrogante entonces A cuánto equivale

la pendiente miren vamos a reescribir

esta función por acá y es igual debido a

que no aparece la pendiente significa

que es 0 0 x Porque si multiplicamos 0

por x nos queda 0 Y al final el cero no

hace falta escribirlo luego debemos

copiar menos 6 Así que acá ya podemos

distinguir el valor de la pendiente y el

valor del término independiente M es

igual a cero y b es igual a menos 6 y

con esto prácticamente hemos terminado

con la primera actividad Espero que les

haya parecido interesante bueno en este

punto vamos a hablar un poquito más a

detalle sobre la pendiente como ya

sabemos su símbolo es la letra m

minúscula y es el grado de inclinación

de la recta respecto al eje de las

abscisas o eje x y se pueden dar tres

casos

que la Gráfica sea creciente constante o

decreciente esto depende del valor de la

pendiente si la pendiente es un número

positivo es decir la pendiente es mayor

a cero la Gráfica es creciente y la

podemos representar de la siguiente

manera por acá tenemos un ejemplo una

recta creciente Ahora si la pendiente M

es igual a cero significa que la recta

es constante por acá tenemos un ejemplo

de cómo se vería la representación

gráfica prácticamente se trata de una

recta horizontal y el tercer caso se da

cuando la pendiente tiene un valor

negativo es decir la pendiente es menor

a cero Lo que sucede es que la recta

será decreciente

muy bien y antes de continuar veamos un

pequeño resumen si la pendiente es mayor

a cero la recta es creciente si la

pendiente es igual a cero la recta es

constante y si la pendiente es menor a

cero la recta es decreciente ahora

Hablemos del término independiente cuyo

símbolo es la letra b minúscula es el

punto de intersección de la recta con el

eje de las ordenadas es decir con el eje

y analicemos las siguientes gráficas nos

ubicamos en el eje y en el eje vertical

y vemos por qué punto pasa la recta y

bueno en esta primera gráfica observamos

que la recta corta por un valor positivo

al eje y este valor a mi gastos que

puede ser uno dos tres corresponde al

valor de B Es decir si ves igual a 5

significa que la recta pasa por y igual

a 5 por acá tenemos el término

independiente para una función constante

y en esta tercera gráfica también vemos

Que B Es un valor positivo en y ahora

pasemos a la siguiente actividad para

comprender mucho mejor estos conceptos

bueno en esta actividad muy interesante

lo que vamos a hacer es un bosquejo de

la Gráfica de cada una de estas

funciones atención que la Gráfica con

esa actitud aún no la podemos encontrar

porque para ello debemos elaborar una

tabla de valores o algunos de los

métodos que más adelante les voy a

mostrar pero al conocer y al identificar

la pendiente y el término independiente

si podemos realizar un bosquejo muy

aproximado de la Gráfica real entonces

empecemos primero como ya vimos en la

sección anterior la pendiente nos indica

si la Gráfica es creciente decreciente o

constante dependiendo del signo de la

pendiente entonces en esta función

observamos que la pendiente tiene signo

positivo se trata de una recta creciente

lo que significa que su comportamiento

es de la la siguiente manera miren una

gráfica creciente algo esencial que

deben conocer Es que esto de constante

creciente o decreciente recibe el nombre

de monotonía y se analiza de izquierda a

derecha y bueno ya analizamos la

pendiente ahora analicemos el término

independiente como les mencioné este

valor nos indica el punto de corte de la

recta con el eje Y en este caso nos está

indicando que la recta pasa por -1 en Y

entonces la vamos a bajar hasta

encontrarnos con -1 observen muy bien y

así tenemos el bosquejo de la primera

función como acotación al término

independiente también se le conoce como

ordenada al origen y listo hemos

terminado con el primer ejercicio

pasemos a la siguiente función primero

analizamos la pendiente en este caso el

valor es menos 2 un número negativo lo

que significa que la recta es

decreciente la Gráfica tendrá el

siguiente comportamiento

como les mencioné la monotonía se

analiza de izquierda a derecha y vemos

que la Gráfica de izquierda a derecha es

decreciente ahora nos vamos con el

término independiente es 4 positivo

significa que la Gráfica corta en el eje

y por el valor de cuatro positivo en

este caso debemos subir nuestra gráfica

hasta el valor de 4 excelente y así es

como queda el bosquejo de la segunda

función Qué sucede acá y es igual a -3x

está claro que la pendiente es -3 un

número negativo y ya sabemos que la

monotonía de esta gráfica es decreciente

entonces ubicamos nuestra recta pero

como ya vimos en actividad número uno

cuando acá no tenemos ningún valor

significa que el término independiente

equivale a 0 En conclusión la Gráfica

debe pasar por el origen de coordenadas

Ya que en este caso en el origen de

coordenadas y es igual a cero Así que

bajamos nuestra querida función muy bien

y vean esta maravilla así se comporta

nuestra función por favor nunca se

olviden que al no tener el término

independiente significa que la Gráfica

pasa por el origen de coordenadas

finalmente tenemos y igual a menos 1 y

como ya estudiamos se trata de una

función constante la pendiente es igual

a cero porque no se visualiza la

variable x y cuando la pendiente es

igual a cero se trata de una recta

horizontal pero atención el término

independiente es -1 lo que significa que

nuestra recta debe pasar o cortar por

menos uno en y por lo tanto debemos

bajar la Gráfica hasta llegar a menos 1

excelente y es así como se representa

gráficamente la función constante y

igual a menos 1 pero miren muchachos

aquí ya no se trata de un bosquejo sino

de la Gráfica real porque para graficar

una función constante no hace falta

tabla de valores y por hoy hemos

terminado con la primera clase sobre

función lineal por favor estar atentos a

las siguientes clases porque van a estar

muy pero muy interesantes sin más

continuaremos practicando repasando

estudiando en el caso de que tengan

alguna duda déjenlo en los comentarios

cuídense mucho y amor y paz

[Música]