KVL and KCL (Circuits for Beginners #11)

Summary

This video covers Kirchhoff's Voltage Law (KVL) and Kirchhoff's Current Law (KCL), explaining these fundamental concepts in electrical circuits. KVL states that the sum of voltages around any closed loop must equal zero, while KCL asserts that the total current entering a junction equals the current leaving it. Through a detailed example, the video demonstrates how to apply these laws to solve circuit problems, including handling voltage polarities and current directions. Viewers gain practical insights into how these laws are used to analyze and solve circuit equations.

Takeaways

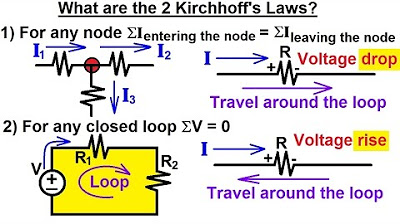
• 😀 Kirchhoff's Voltage Law (KVL) applies to all circuit elements, whether linear or nonlinear, and ensures that the sum of the voltages around any closed loop equals zero.
• 😀 KVL can be applied to both simple and complex circuits, as demonstrated with a loop containing a voltage source, resistors, and unknown elements.
• 😀 The polarity of voltage labels is important for consistency, but incorrect polarity will result in a negative value for the calculated voltage.
• 😀 When applying KVL, voltages must be labeled with their polarities to ensure correct calculation, even if the exact direction of current is unknown.
• 😀 Kirchhoff's Current Law (KCL) states that the sum of currents entering a junction must equal the sum of currents leaving the junction, ensuring conservation of charge.
• 😀 The direction of current can be arbitrarily labeled in circuit analysis, and if the polarity or direction is wrong, the result will simply be a negative value for the current.
• 😀 The distinction between current sources and labeled currents is important: current sources force a specified current, while labeled currents are simply measurements.
• 😀 When using KVL, it's crucial to avoid crossing current sources in the loop, as their voltage is variable and not defined by Ohm's Law.
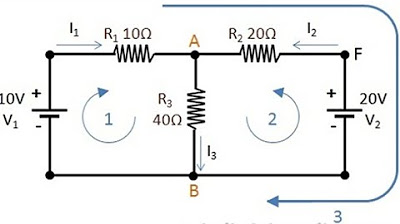
• 😀 To solve circuits with multiple unknowns, both KVL and KCL must be applied together, leading to simultaneous equations that can be solved for the unknowns.
• 😀 In a more complex example, KVL and KCL were applied to solve for unknown currents in a circuit involving a DC voltage source, resistors, and a current source, demonstrating how both laws can be used in tandem for circuit analysis.

Q & A

What does Kirchhoff's Voltage Law state?

Kirchhoff's Voltage Law (KVL) states that in any given loop in a circuit, the sum of all voltages must equal zero. This means that the total voltage gained as you move around the loop must be balanced by the total voltage lost, ensuring no net voltage exists at the start and end of the loop.

What is the significance of polarity when applying Kirchhoff's Voltage Law?

Polarity is crucial in determining the direction of voltage rises and falls. While the exact labeling of voltage polarities does not affect the outcome of KVL, consistency is essential. If the polarity is chosen incorrectly, the calculated voltage will simply be negative.

How do you handle unknown circuit elements when applying KVL?

When dealing with an unknown circuit element, you can represent it as a placeholder, such as a box. This allows you to apply Kirchhoff’s Voltage Law while leaving the specific characteristics of that element undefined until more information is available.

What happens if the polarity of a voltage is labeled incorrectly in a circuit?

If the polarity is labeled incorrectly, the calculated voltage for that element will simply have a negative value. The overall result remains valid because the sign will reflect the direction of the voltage, not the labeling.

What does Kirchhoff's Current Law state?

Kirchhoff’s Current Law (KCL) states that the sum of currents entering a junction in a circuit must equal the sum of currents leaving the junction. This is often summarized as: 'Current in equals current out.'

How can the Kirchhoff Current Law be applied in a circuit problem?

To apply KCL, you analyze a junction where currents converge or diverge. The sum of the incoming currents must equal the sum of the outgoing currents. This relationship can help solve for unknown current values at the junction.

In the example circuit with 2 amperes and 3 amperes of current, how do we find the unknown current?

In the given example, the Kirchhoff Current Law is applied by noting that the incoming current is 2 amperes, and the outgoing current is 3 amperes. The unknown current is calculated as -1 ampere, indicating that current flows in the opposite direction than initially assumed.

What is the difference between labeled current in the circuit and a current source?

The labeled current represents a measurement of current passing through a resistor or wire, while a current source actively controls and forces a certain amount of current to flow in a circuit. The labeled current does not dictate the current but rather reflects the conditions set by other elements in the circuit.

What role does Ohm's Law play in Kirchhoff’s Voltage Law?

Ohm’s Law (V = IR) helps determine the voltage drops across resistive elements in the circuit. When applying KVL, the voltage drop across each resistor can be calculated using Ohm’s Law, which allows for a more accurate application of the voltage law.

Why is it problematic to include a current source when applying Kirchhoff's Voltage Law?

Current sources introduce a variable voltage drop, making it difficult to apply Kirchhoff’s Voltage Law across them. Since the voltage across a current source depends on other circuit elements, it doesn't have a fixed value that can be easily incorporated into a voltage loop calculation.