HUKUM II KIRCHHOFF

Summary

This educational video script delves into Kirchhoff's Laws, specifically focusing on Kirchhoff's Voltage Law (KVL). It explains how the sum of potential differences in a closed circuit equals zero, indicating no energy loss within the circuit. The script guides viewers through applying KVL to analyze circuits, using illustrations to clarify concepts. It also outlines rules for determining the direction of loops and the sign of voltage drops, crucial for solving electrical circuit problems. The tutorial aims to simplify the understanding and application of KVL, encouraging viewers to engage with the material and seek further clarification if needed.

Takeaways

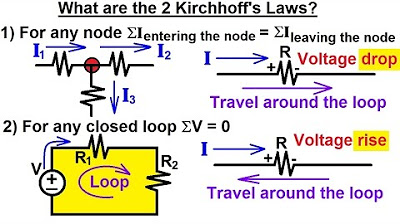
• 😀 The video discusses the second law of Kirchhoff, also known as Kirchhoff's voltage law (KVL), which states that the sum of the voltages in a closed circuit is equal to zero.
• 🔌 The law applies to non-branching circuits, as opposed to the first law of Kirchhoff, which deals with current in branching circuits.
• 🔋 Kirchhoff's second law is fundamental in analyzing the potential difference in a closed electrical circuit, ensuring that the total energy in the circuit is conserved with no energy being lost.
• 📚 The mathematical representation of KVL is given by the equation ΣV = 0, where V represents the voltage drops and sources in the circuit.
• 👉 The direction of the loop in the circuit can be chosen arbitrarily, but it's recommended to align it with the direction of the current for ease of calculation.
• ⚡ When the direction of the loop is the same as the direction of the current, the voltage drop is considered positive; if opposite, it is negative.
• 🔄 If the loop encounters a positive terminal first, the electric current direction should also be positive; conversely, if a negative terminal is encountered first, the current direction should be negative.
• 📉 The law helps in solving for unknown currents and voltages in electrical circuits by setting up equations based on the conservation of energy.
• 📝 An example problem is solved in the script, demonstrating how to apply KVL to find the current flowing through a circuit with given resistors and voltage sources.
• 🤔 The video encourages viewers to ask questions if they have difficulties understanding the material, offering multiple communication channels for clarification.

Q & A

What is the main topic discussed in the script?

The main topic discussed in the script is Kirchhoff's laws, specifically focusing on Kirchhoff's second law, also known as Kirchhoff's voltage law (KVL).

What is Kirchhoff's first law about?

Kirchhoff's first law, also known as Kirchhoff's current law (KCL), states that the total current entering a junction in a circuit is equal to the total current leaving the junction.

What does Kirchhoff's second law (KVL) imply about the sum of the voltages in a closed circuit?

Kirchhoff's second law (KVL) implies that the sum of the voltages (potential differences) in a closed circuit is equal to zero, indicating that there is no loss of energy in the circuit.

What is the mathematical expression for Kirchhoff's second law in terms of voltages?

The mathematical expression for Kirchhoff's second law is ΣV = 0, where the sum of all the voltages (potential differences) around a closed loop is zero.

How does the script differentiate between the application of Kirchhoff's first and second laws?

The script differentiates by stating that Kirchhoff's first law is applied to circuits with branches (junctions), while the second law is applied to analyze the potential differences in a closed circuit without branches.

What is the significance of the direction of the loop in applying Kirchhoff's second law?

The direction of the loop is significant because it determines the sign of the potential difference when applying Kirchhoff's second law. If the loop direction is the same as the current flow, the potential difference is positive; if opposite, it is negative.

What is the practical application of Kirchhoff's laws in solving electrical circuit problems?

Kirchhoff's laws are used to analyze and solve complex electrical circuits by providing a systematic method to calculate unknown currents and voltages in the circuit.

How does the script suggest determining the direction of the current flow for easier calculations?

The script suggests that for easier calculations, the direction of the loop should preferably be the same as the direction of the current flow, although it can be chosen freely.

What is the importance of understanding the sign of the potential difference in a circuit?

Understanding the sign of the potential difference is important because it indicates whether the energy is being absorbed or supplied in a part of the circuit, which is crucial for correctly applying Kirchhoff's second law.

Can you provide an example from the script where Kirchhoff's second law is applied to calculate the current in a circuit?

Yes, the script provides an example with three resistors (R1=2Ω, R2=6Ω, R3=4Ω) and two voltage sources (6V and 12V). It uses Kirchhoff's second law to set up an equation and solve for the current, which is found to be 0.5 amperes.

Outlines

00:00

🔌 Introduction to Kirchhoff's Second Law

The script begins with a casual greeting and introduces the topic of Kirchhoff's laws, specifically focusing on the second law, often referred to as Kirchhoff's voltage law (KVL). It contrasts this with Kirchhoff's first law, which deals with current conservation at junctions. The second law discusses the conservation of energy within a closed circuit, stating that the sum of all voltages (potential differences) in the circuit equals zero. This implies no energy is lost and all is utilized within the circuit. The explanation is set to be accompanied by illustrations to clarify the concept.

05:03

📚 Explanation of Kirchhoff's Second Law and Its Application

This paragraph delves into the mathematical formulation of Kirchhoff's second law, explaining that the algebraic sum of the potential differences around a closed loop is zero. It provides a step-by-step guide on how to apply this law to analyze circuits, including choosing a loop direction and understanding the sign of voltage drops based on the direction of the loop relative to the current flow. The explanation includes rules for determining whether a voltage drop is positive or negative, which depends on the alignment of the loop direction with the current flow.

10:04

🔍 Practical Application of Kirchhoff's Second Law in Circuit Analysis

The script continues with a practical example of applying Kirchhoff's second law to a circuit with three resistors and two voltage sources. It outlines the process of setting up the equation based on the law, taking into account the direction of the loops and the polarity of the voltage sources. The example demonstrates how to calculate the current flowing through the circuit by summing the voltage drops and the product of current and resistance for each component, setting the equation to equal zero and solving for the unknown current.

15:05

📝 Conclusion and Invitation for Further Queries

The final paragraph wraps up the discussion by summarizing the solution to the example problem, which calculated the current in the circuit to be 0.5 amperes. It encourages viewers who have difficulties or questions to reach out via WhatsApp, Telegram, or by commenting on the video for further clarification. The script ends with well-wishes for the viewers' health and success in their tasks, followed by a traditional closing greeting.

Keywords

💡Kirchoff's Laws

Kirchoff's Laws are fundamental principles in electrical circuit theory, consisting of Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL). In the video, the focus is on Kirchhoff's Voltage Law, which states that the algebraic sum of the potential differences (voltages) in a closed loop or circuit is zero. This law is essential for analyzing and solving complex electrical circuits, as illustrated by the script's discussion on calculating currents and voltage drops in a given circuit.

💡Potential Difference

Potential difference, often referred to as voltage, is the work needed per unit of charge to move a test charge between two points. In the context of the video, potential difference is used to describe the driving force for the electric current in a circuit. The script mentions analyzing potential differences across various components within a closed circuit, which is a key aspect of applying Kirchhoff's Voltage Law.

💡Closed Circuit

A closed circuit is an electrical path where the current has a continuous and unbroken route, allowing the flow of electric charge without any interruption. The video script discusses the application of Kirchhoff's Voltage Law specifically to closed circuits, emphasizing that the total voltage around such a circuit sums up to zero.

💡Ohm's Law

Ohm's Law is a basic principle that relates voltage (V), current (I), and resistance (R) in an electrical circuit, expressed as V = IR. Although not explicitly named in the script, the concept is implied when discussing the relationship between voltage drops across resistors and the current flowing through them in the circuit analysis.

💡Resistor

A resistor is a passive component in an electrical circuit that opposes the flow of current, converting electrical energy into heat. The script mentions different resistors with values such as 2 Ohms, 6 Ohms, and 4 Ohms, which are used to calculate voltage drops and currents in the circuit.

💡Voltage Source

A voltage source is a device that provides a potential difference to drive the flow of current in a circuit. The video script refers to two voltage sources with values of 6 volts and 12 volts, which are integral to the application of Kirchhoff's Voltage Law in the circuit analysis.

💡Electric Current

Electric current is the flow of electric charge in a circuit, typically measured in amperes (A). The script discusses calculating the current flowing through a circuit as part of the application of Kirchhoff's laws, with an example calculation resulting in a current of 0.5 amperes.

💡Circuit Analysis

Circuit analysis is the process of determining the behavior of an electrical circuit, such as the current and voltage at each point. The video script provides a detailed example of circuit analysis using Kirchhoff's Voltage Law to calculate the current in a circuit with specified resistors and voltage sources.

💡Algebraic Sum

The algebraic sum refers to the total obtained by adding numbers considering their signs, which can be positive or negative. In the video, the concept is used to explain that the sum of all potential differences in a closed circuit, when calculated algebraically, equals zero according to Kirchhoff's Voltage Law.

💡Electric Energy

Electric energy is the energy derived from the flow of electric power, which is the rate at which electric work is done. The script mentions that according to Kirchhoff's Voltage Law, there is no electric energy wasted in a closed circuit, as all energy is absorbed and used, which is a fundamental concept in the conservation of energy.

💡Conductor

A conductor is a material that allows the flow of electric charge, thus enabling the movement of electric current. While the term 'conductor' is not explicitly mentioned in the script, the concept is inherent in the discussion of electric current flowing through components like resistors, which can be considered a type of conductor with specific resistance properties.

Highlights

Introduction to Kirchhoff's laws, specifically focusing on Kirchhoff's second law, also known as Kirchhoff's voltage law (KVL).

Explanation of Kirchhoff's first law, which states that the total current entering a junction is equal to the total current leaving the junction.

Kirchhoff's second law discusses the conservation of energy within a closed circuit, where the sum of the voltages around the circuit equals zero.

Illustration of the concept of voltage drops and rises in a closed circuit, emphasizing the conservation of energy.

The mathematical formulation of Kirchhoff's second law, expressed as the sum of algebraic differences in voltage being equal to zero.

A practical example of applying Kirchhoff's second law to a simple circuit with three resistors and two voltage sources.

Detailed step-by-step calculation process for determining the current in a circuit using Kirchhoff's second law.

The importance of choosing the correct loop direction for simplifying the calculation process in circuit analysis.

Rules for determining the positive or negative sign of voltage drops in a circuit based on the direction of the current flow.

The impact of the initial encountered terminal on the sign of the electric force (voltage) in the circuit analysis.

Guidance on how to approach problems involving Kirchhoff's second law, including tips for selecting loop directions and interpreting voltage signs.

A specific problem-solving example involving a circuit with given resistor values and voltage sources, demonstrating the application of Kirchhoff's second law.

Calculation of the current flowing through a circuit using the derived formula from Kirchhoff's second law.

Emphasis on the conservation of energy in electrical circuits, where no energy is lost, and all is absorbed and used.

Invitation for viewers to ask questions or seek clarification on Kirchhoff's laws through various communication channels.

Closing remarks with well-wishes for health and success in tasks, encouraging the application of the learned concepts in practice.

Transcripts

yo yo Wega selamat berjumpa lagi dengan

Bapak di sini gimana kabarnya mudahan

baik-baik saja sehat selalu ya bahagia

lahir dan batin itu yang kita harapkan

bersamanya Dan untuk kesempatan kali ini

kita akan membahas tentang hukum

Kirchoff tapi untuk kali ini kita akan

membahas tentang hukum dua pistol Nah

setelah di konten Sebelumnya kan kita

membahas tentang hukum 1 Kirchoff kalau

hukum 1 Kirchoff itu membahas tentang

harusnya ya jadi arus yang masuk kedalam

suatu didik

gabungan itu sama dengan jumlah arus

yang keluar dari titik percabangan

tersebut itu hukum satunya untuk hukum2

pitstop itu lebih luas tentang kepada

tegangannya ya jadi sumber tegangan atau

beda potensial yang ada di dalam suatu

rangkaian tertutup itu jika dijumlahkan

semuanya akan sama dengan nol yang

artinya energi yang ada di dalam

rangkaian tersebut itu diserap kemudian

gunakan diserap digunakannya gitu ya Eh

jadi artinya tidak ada energi yang

terbuang bisa dijumlah tegangannya untuk

bergerak listriknya itu sama dengan nol

untuk lebih jelasnya marilah kita ikuti

ilustrasi dan pembahasan berikut ini

di media coba tabat saya hukum 2

Kirchoff hukum 2 Kirchoff ini berlaku

pada rangkaian yang tidak bercabang

berbeda dengan hukum 1 Kirchoff yang

kalaupun satu besok kan pada rangkaian

yang bercabang Nah untuk hukum 2

Kirchoff ini digunakan untuk

menganalisis beda potensial yang terjadi

pada

Hai rangkaian yang tertutup

hai eh sehingga karena tidak potensial

yang dipelajari atau tegangan yang

dipelajari dalam rangkaian tertutup ini

hukum 2 Kirchoff itu lebih terkenal

dengan hukum tegangan Kirchoff ya

Hai atau bahasa merekanya gitu Kirchoff

voltage slow gitu ya disingkat kvl gitu

Ya udah bunyi hukum dot kecap adalah

Jumlah aljabar beda potensial atau

tegangan pada suatu rangkaian tertutup

adalah sama dengan nol itunya dijumlah

beda potensialnya jika dijumlahkan semua

itu akan =

Hai kemudian versi lain dari hukum.co.id

ini pada rangkaian tertutup berbunyi

Hai jumlah aljabar gerak listrik dan

jumlah penurunan tegangannya itu sama

dengan nol sehingga secara matematika

bisa ditulis Sigma epsilon ya kecil itu

dijumlahkan dengan sigmatic kali er

Italia itu tegangannya itu sama dengan

nol di segment silon plus Sigma i * r

itu sama dengan nol Oke untuk lebih

jelasnya kita perhatikan ilustrasi

berikut ini ya Nah ini dia gambarnya

dari hukum 2 Kirchoff sana ada gambar

rangkaian yang tertutup ya Eh yang

berwarna hijau apa ya di tengah itu dan

itu terjadi lingkaran dengan tanda panah

melingkar searah jarum jam itu ya itu

namanya lupa nanti jadi lupa itu ada

lingkaran mau

yaitu searah jarum jam oleh makhlukNya

itu berlawanan arah jarum jam juga boleh

nanti lupa adalah lingkaran yang ada di

dalam rangkaian tertutup tersebut ya gak

melingkarnya nya jadi berdasarkan

gambarnya ya terlihat gambar disana ada

daerah a-kembar Dian ke b ke c gede gitu

ya berdasarkan gambar tuh total tegangan

pada rangkaian adalah Ed tegangan dari a

ke b ya kemudian tegangan dari B ke c

dengan dari ceday tegangan dari BK itu

sama dengan nol Jadi kalau ditulis

matematis ppab Plus

Hai + VCD + Pi Dea itu sama dengan nol

itu ya kalau ditulis matematik hukum 2

Kirchoff ini menjelaskan bahwa jumlah

penurunan beda potensial itu sama dengan

nol itu artinya itu tidak ada energi

yang hilang dalam rangkaian ini ya atau

semua energi listrik itu diserap dan

digunakan itu ya

Hai deh Ya itu pemaparan untuk Apa itu

hukum 2 Kirchoff atau kesimpulan dari

hukum 2 Kirchoff ya kemudian kita ke

persyaratan tandanya ya nanti nantikan

kita mau mengerjakan soal-soal tentang

hukum 2 Kirchoff ini ada yang positif

atau negatif gitu ya untuk menentukan

positif negatifnya bagaimana nanti ya

kayak kita ikuti pemaparan berikut ini

ini dia ya langsung kita baca ya

aturan-aturannya supaya nanti ketika

mengerjakan Soalnya kita bisa dengan

mudah yang menghitungnya enggak kita

sahabat saya

Hai untuk menganalisis suatu rangkaian

listrik menggunakan hukum.id top

diperlukan beberapa aturan atau

perjanjian yang pertama pilih lup-lup

itu lingkaran yang di tengah itu ya

untuk masing-masing lintasan tertutup

dengan alat tertentu

Hai jadi nanti arahnya bebas saya boleh

searah jarum jam itu ya lingkarannya

boleh juga berlawanan arah jarum jam

Hai tapi Jika memungkinkan usahakan

nanti arahnya searah dengan arah arus ya

nge-rap supaya lebih mudah ya nanti

untuk menentukan perhitungannya gitu ya

jadi eh mau searah jarum gak mau

berlawanan Azzam bertarung jam itu

sebetulnya bebas-bebas aja boleh-boleh

saja tapi untuk lebih mempermudah nya

usahakan nanti arahnya itu searah dengan

arus gitu ya nanti kita akan paham kalau

kita sedang mengerjakan soalnya Ya nah

yang nomor dua itu pada suatu cabang

ilmu

Hai jika arah Loop sama dengan arah arus

maka penurunan tegangan bertanda positif

Jadi kalau misalkan arah luknya searah

jarum jam sementara arah arusnya juga

searah jarum jam gitu ya Nah maka apa

penurunan tegangannya bertanda

Hai Positif itu ya Kalau arah luknya

searah dengan arus tapi jika berlawanan

dengan arah arus maka arah tegangannya

bertanda negatif kalau misalkan lu punya

searah jarum jam nih lihat gambarnya itu

yang kedua

Hai kalau misalkan arahnya searah jarum

jam itu ya terus arah arusnya juga

searah jarum jam

Hai makan nanti eh penurunan tegangan

Nyai kali airnya positif Karena

sama-sama searah gitu ya tuh yang aturan

nomor

Hai the

Hai terlihat aturan nomor satu tuh kan

gambarnya ada dua jadi ada arah Loop

yang searah jarum jam itu ya ada arah

Aduh ada arah Loop yang berlawanan arah

jarum jam itu hanya gambar cara jarum

jam itu aja berlawanan arah jarum jam

gitu aja ya Jadi untuk Gang nomor satu

mah itu aturannya ya mau searah boleh

mau berlawanan arah juga boleh tapi

Usahakan kalau bisa searah dengan arah

arus makhluk-nya gitu Nah untuk aturan

yang kedua ini hehehe

Hai ini hanya menentukan tanda positif

dan tanda negatif di Sudah tadi Ya

sekelas B pada suatu cabang jika arah

Loop sama dengan arah arus maka

penurunan tegangannya bertanda positif

lu gambar yang pertama ini bertanda

positif di jika lingkaran luknya itu

searah dengan arah arus gambar yang

kedua ini kalau misalkan lu punya

berlawanan dengan arah jarum jam atau

berlawanan dengan arah arus Maka nanti

tegangannya itu bertanda negatif jadi er

negatif Nah itu

Hai tutup aturan yang kedua loh

Hai perjanjian yang kedua kemudian ada

lagi perjanjian yang ketiga yaitu jika

saat mengikuti arah Loop kutub sumber

tegangan yang lebih dahulu dijumpai

adalah kutub positif maka gaya gerak

listrik nya juga harus bertanda positif

nah sebaliknya jika kutub yang lebih

dahulu dijumpai adalah kutub negatif

maka gaya gerak listrik nya juga

bertanda negatif Betul dek ketika klub

itu berputar ya kemudian dia bertemu

dengan kutub positif maka GGL nya juga

harus positif gitu ya Tapi ketika

dial-up nyamuk memutar yang pertama itu

ketemu kutub negatif Nah maka GGL nya

juga harus bertanda negatif itu berapa

perjanjian yang Rudi sepakat tidur

ya sebelum kita mengerjakan soal-soal

tentang hukum 2 Kirchoff ini ya oke baik

untuk lebih jelasnya kita gunakan

aturan-aturan tersebut saat kita nanti

mengerjakan soal-soalnya oke langsung

saja kita ke soalnya

hai hai

di media soal yang pertama tentang hukum

Kirchoff

Ayo kita lihat gambarnya ya

Hai disana ada tiga buah resistor dan

ada dua buah sumber tegangan gaya gerak

listrik ya dimana arusnya itu berarah

berlawanan arah jarum jam yang lihat di

bawah arahnya gitu ya

Hai ditambah panahnya ke kanan kemudian

Ya nantinya akan memutar berlawanan arah

jarum jam arah harusnya ya dan arah

luknya juga berlawanan arah jarum jam

kayaknya

Hai jadi ini arah luknya sudah searah

dengan arah harusnya kemudian apa saja

yang diketahui dari gambar tersebut ada

R1 ya resistor yang pertama itu dua Om

kemudian R2 resistor yang kedua itu 6

Ohm dan R3 4omh gitu Kemudian untuk GGL

satunya 6volt dan untuk GGL keduanya 12

volt langsung saja ya kita ke rumus dari

hukum 2 Kirchoff hukum 2 Kirchoff

berbunyi jumlah GGL dan sumber tegangan

itu harus sama dengan nol Ya adek

the country's matematik Disana sudah ada

jawabannya Sigma F Sigma epsilon gitu ya

ditambah Sigma Ikal er itu =

Hai Sigma epsilon atau Sigma itu ya

Semua GGL yang ada untuk GGL yang

pertama itu yang 12 volt dari dari bawah

dulu ya Jadi kita ngitungnya dari bawah

dulu dari yang 12 volt itu sebagai

Google pertama yang dihitung pada Geger

satunya akan yang 60 tapi webassign

namanya penjumlahannya boleh dari yang

mana saja akan bebas jadi mint epsilon 2

kenapa minus Nah karena tanda aloe pnya

itu

hai pertama ketemu dengan tanda minus

gitu pertama dengan ketemu dan kutub

negatif jadi untuk GGL dua itu min min

epsilon 2 ditambah plus epsilon satu ya

karena Lubna di epsilon Sabtu ketemu

Positif itu plus i * r 3 plus ya karena

klubnya searah dengan arah arus kemudian

plus kali ilir2 plus juga ya + I * R1 =

0 sekarang tingkat kita tinggal masukkan

angka-angkanya ke dalam rumusnya gitu ya

Di epsilon 2-12 epsilon

Hai yang ditanyakan R34 r26 dan er

satunya dua sehingga setelah kita ganti

rumusnya dengan angka-angka menjadi mint

12 + enam plus e4plus E6 + I2 = 0 itu

kemudian min12 ditambah enam itu

menamkan kemudian yang ada isinya itu

dijumlahkan semua 4 + 6 10 10 Plus 2 12

sehingga hasilnya 12 in610 dengan

Hai sehingga dengan persamaan ini kita

bisa mencarinya menghitung iya jadinya =

6 per-12 hasilnya adalah 0,5 ampere

terjawablah sudah ya ya pertanyaannya

karena yang ditanyakan deh soal ini

adalah arus yang mengalir dalam

rangkaian nih jadi harusnya adalah 60120

= 0,5 sampai ke itu satu contoh soal

semoga kalian mudah memahaminya ya Dan

apabila ada yang belum paham atau tidak

mengerti

Hai oleh kalian Japri lewat WA lewat

telegram atau seperti biasa oleh kalian

Comment di bawah video ini nah Tadinya

sih mau bahas beberapa soalnya Tapi

kalau perhitungkan ini akan menambah

durasi dan untuk menghemat kuota ya oke

Bila kalian ada misalkan menemukan soal

yang lain tentang hukum 2 Kirchoff dan

tidak kesulitan boleh kalian tanyakan

langsung ya lewat Japri atau kalian bisa

komen di bawah video ini tidak jaya

untuk kali ini mudah-mudahan semuanya

diberikan kesehatan kelancaran dalam

mengerjakan tugas-tugasnya Billahi

taufik wal hidayah wassalamualaikum

warohmatullohi wabarokatuh