Kirchhoff's Voltage Law (KVL) - How to Solve Complicated Circuits | Basic Circuits | Electronics

Summary

This video script offers a comprehensive exploration of Kirchhoff's Voltage Law (KVL) and its application in mesh analysis for electrical circuits. It explains the fundamental principle that the sum of voltages in a closed loop equals zero, contrasting it with Kirchhoff's Current Law. The tutorial walks through steps for applying KVL, from intuitive understanding to assigning mesh currents, formulating equations, solving simultaneous equations, and conducting a sanity check. The script includes examples to illustrate the process and emphasizes the importance of consistency and verification in calculations.

Takeaways

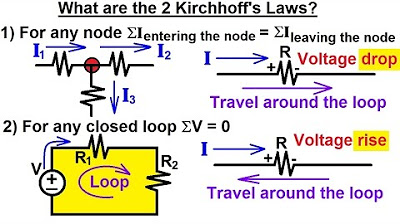
• 📚 The script introduces Kirchhoff's Voltage Law (KVL), which states that the sum of all voltages in a closed loop or mesh equals zero.
• 🔍 Kirchhoff's Current Law (KCL) is mentioned for comparison, emphasizing that it deals with the conservation of charge at nodes, while KVL focuses on voltage drops in loops.
• 🤔 The script acknowledges that the intuitiveness of KVL can vary among electrical engineers, suggesting personal preference may affect one's approach to circuit analysis.
• 👨‍🏫 The presenter provides a step-by-step guide on how to apply KVL, including setting up equations based on voltage drops and rises across components within a loop.
• 🔧 The importance of assigning consistent directions for mesh currents is highlighted to avoid confusion and errors in the analysis.
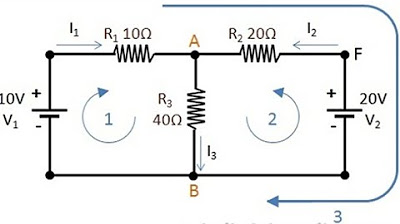
• 🔄 The script explains that mesh analysis requires loops that do not include one another, ensuring that each loop is independent for the analysis.
• 📝 An example is given to demonstrate the process of applying KVL, including assigning mesh currents, setting up equations, and solving them.
• 🧠 The presenter emphasizes the importance of a 'sanity check' after solving the equations to ensure the results are reasonable and make sense in the context of the circuit.
• 🔢 The script mentions the use of matrix calculations or calculators to solve simultaneous equations, which can simplify the process and reduce the chance of mathematical errors.
• 🔗 Additional resources and examples are available on the website 'circuitbred.com' for those who wish to deepen their understanding of KVL and circuit analysis.
• 👍 The presenter encourages viewers to like, subscribe, and follow for more tutorials on basic circuits, indicating ongoing educational content.

Q & A

What is Kirchhoff's Current Law (KCL)?

Kirchhoff's Current Law states that the total current flowing into any node (junction) in an electrical circuit is equal to the total current flowing out of that node. Essentially, it means the sum of currents at a node equals zero.

What is Kirchhoff's Voltage Law (KVL)?

Kirchhoff's Voltage Law states that the algebraic sum of all the voltages in a closed loop or mesh in a network is zero. This is based on the conservation of energy principle.

What is the basis of mesh analysis in electrical circuits?

Mesh analysis is based on Kirchhoff's Voltage Law (KVL), which is used to analyze circuits by setting up equations for each mesh (loop) in the circuit and solving for unknown voltages or currents.

Why is it important to assign a direction for mesh currents?

Assigning a direction for mesh currents is crucial for consistency when setting up equations. It helps in correctly applying KVL, as the voltage drops or rises across components must be considered with respect to the assumed direction of current flow.

How does one determine the mesh currents in a circuit?

To determine mesh currents, one must first identify all the independent loops or meshes in the circuit. Then, assign a direction of flow for each mesh current, keeping in mind that the actual direction may be opposite, but the analysis remains consistent.

What is the purpose of setting up equations for each mesh in a circuit?

Setting up equations for each mesh allows you to express the relationship between voltages and currents in the circuit using KVL. These equations are then solved to find the unknown currents or voltages in the circuit.

How can one solve the equations obtained from mesh analysis?

The equations can be solved using algebraic methods or by employing a matrix approach, such as setting up a system of linear equations and using a matrix calculator or software to find the values of the unknown variables.

What is a sanity check in the context of circuit analysis?

A sanity check is a final step after solving the circuit equations where you verify if the obtained results make sense in the context of the problem. It involves checking if the calculated values are within expected ranges and are physically plausible.

Why is it necessary to ensure that no mesh includes another in mesh analysis?

In mesh analysis, it's important that each mesh is independent and does not include another to avoid redundancy and to ensure that the system of equations is properly set up and solvable.

How does the presence of shared elements affect the setup of equations in mesh analysis?

Shared elements, such as resistors through which multiple mesh currents pass, require careful accounting in the equations. The voltage across the shared element must be considered for each mesh current, often resulting in terms like 'i1 - i2' to represent the net voltage drop or rise.