Định lý giới hạn trung tâm (Central limit theorem)
Summary
TLDRThis video explains the Law of Large Numbers and the Central Limit Theorem, highlighting their importance in probability theory. The Law of Large Numbers demonstrates that as the sample size increases, the sample mean converges to the expected value, and the variance of the mean decreases. The Central Limit Theorem further explores the distribution of sample means, stating that, for large sample sizes, the distribution approaches a normal distribution regardless of the original variable's distribution. Through an Excel example, the video shows how increasing sample size results in a more accurate and bell-shaped distribution of sample means.
Takeaways
- 😀 The Law of Large Numbers states that the average of n independent and identically distributed random variables converges to the expected value of the variable as n increases.
- 😀 As the sample size (n) increases, the variance of the sample mean decreases, making the mean closer to the expected value.
- 😀 The Law of Large Numbers only provides information about the expectation and variance of the sample mean but does not describe the distribution of the sample mean.
- 😀 The Central Limit Theorem (CLT) addresses the distribution of the sample mean, stating that it will approximate a normal distribution as n becomes large, regardless of the original distribution of the data.
- 😀 According to the CLT, for large n, the distribution of the sample mean will have a mean equal to the population mean and a variance equal to the population variance divided by n.
- 😀 Even if the original distribution of the random variable (X) is non-normal, the sample mean distribution will follow a normal distribution for sufficiently large n.
- 😀 The sample size required for the sample mean to approximate a normal distribution depends on the original distribution of X. For distributions closer to normal, smaller sample sizes are sufficient.
- 😀 For skewed or non-normal distributions, a larger n is required to approximate the normal distribution of the sample mean.
- 😀 In practice, a sample size of around 40 is generally considered large enough to observe normality in the sample mean distribution.
- 😀 The Central Limit Theorem also applies to the sum of n independent random variables, where the sum will follow a normal distribution with specific parameters based on the mean and variance of the individual variables.
Q & A
What is the Law of Large Numbers?
-The Law of Large Numbers states that the average of a large number of independent and identically distributed random variables will converge to the expected value of the underlying distribution as the sample size increases.
How does the Law of Large Numbers relate to the expected value of the sample mean?
-As the sample size increases, the sample mean gets closer to the expected value of the random variable. This means that the average of n random variables will converge to the true expected value as n grows large.
What does the Law of Large Numbers tell us about the variance of the sample mean?
-The variance of the sample mean decreases as the sample size increases. Specifically, the variance of the sample mean is the variance of the individual random variables divided by the sample size, meaning it becomes smaller as n grows larger.
Does the Law of Large Numbers provide information about the distribution of the sample mean?
-No, the Law of Large Numbers only provides information about the expected value and variance of the sample mean. It does not describe the distribution of the sample mean.
What is the Central Limit Theorem (CLT) and how does it relate to the Law of Large Numbers?
-The Central Limit Theorem is a development of the Law of Large Numbers. It states that as the sample size increases, the distribution of the sample mean will approach a normal distribution, regardless of the original distribution of the individual random variables.
How does the Central Limit Theorem describe the distribution of the sample mean?
-According to the CLT, as the sample size (n) grows large, the sample mean will follow a normal distribution with the mean equal to the expected value of the individual random variable, and the variance equal to the variance of the individual variable divided by n.
What is the significance of the Central Limit Theorem in probability and statistics?
-The Central Limit Theorem is important because it allows us to make inferences about the population mean using the normal distribution, even when the population distribution is not normal. This makes statistical analysis easier and more accurate, especially for large sample sizes.
What determines when n is considered large enough for the Central Limit Theorem to apply?
-The required sample size for the CLT to apply depends on the distribution of the individual random variable. If the distribution of the variable is already close to a normal distribution, a sample size of 20-30 may be sufficient. For non-normal distributions, a sample size of 40 or larger is typically considered adequate.
Can the Central Limit Theorem be applied if the distribution of the individual variable is highly skewed?
-Yes, the Central Limit Theorem can still be applied, but in such cases, a larger sample size (often 40 or more) is needed for the sample mean to approximate a normal distribution.
What is the relationship between the sample size and the spread of the sample mean distribution?
-As the sample size increases, the spread (or standard deviation) of the sample mean distribution decreases. The standard deviation of the sample mean is the population standard deviation divided by the square root of the sample size, which gets smaller as n increases.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

0625 Independencia de variables aleatorias

Probability and Statistics: Overview
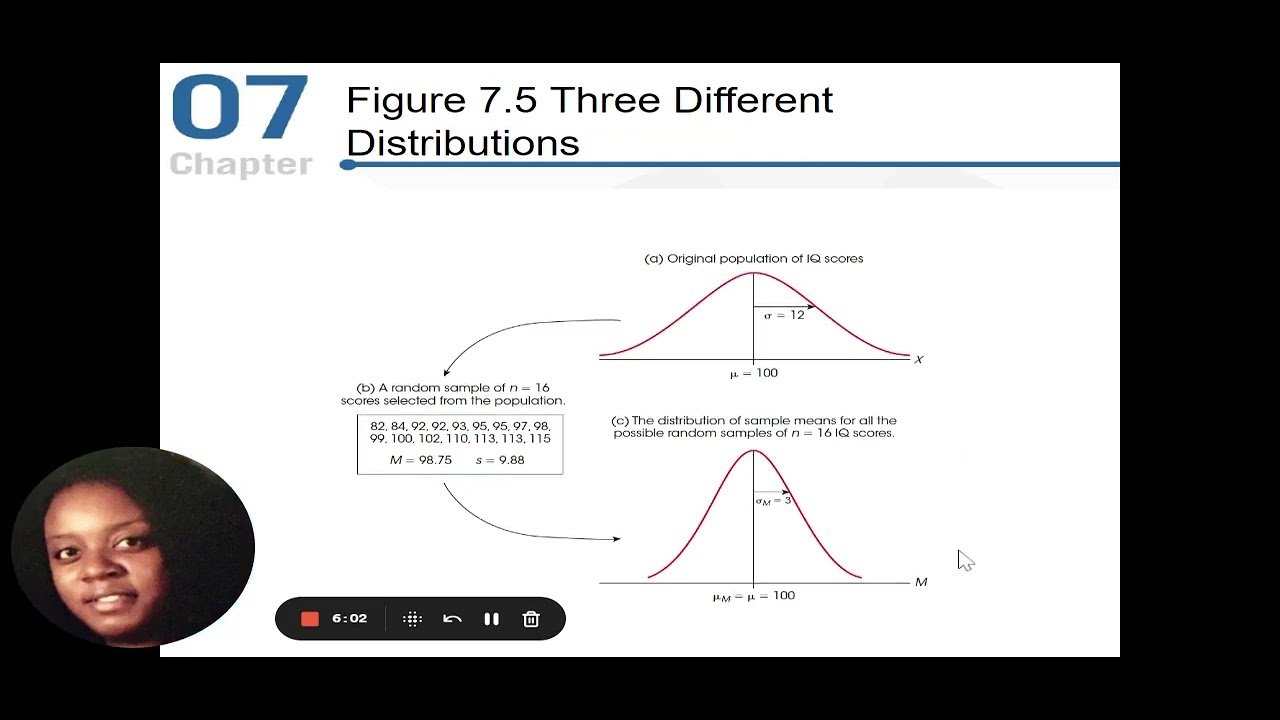
Chapter 7 Probability and Samples The Distribution of Sample Means

Probabilitas dan Statistik: 8.6 Central Limit Theorem

Modul 1.1 - MATERI MODUL 1 DISTRIBUSI PELUANG

Probability Theory L51a Section 5.8 Part 1 Chebyshev's Inequality and Convergence in Probability
5.0 / 5 (0 votes)
