工數期末報告
Summary
TLDRThis presentation delves into the realm of signal analysis through the lens of Fourier Transforms, honoring the contributions of Jean-Baptiste Joseph Fourier. It explains the concept of decomposing periodic functions into simpler oscillating functions, tracing its roots back to ancient astronomy. The mid-1960s breakthrough in Fast Fourier Transforms revolutionized signal processing, enabling efficient analysis with electronic computers. The presentation highlights the Fourier Transform's ability to convert signals from the time domain to the frequency domain, facilitating the analysis of various frequency components. It underscores the wide applications of Fourier Transforms in signal processing, telecommunications, and data analysis, concluding with its utility in analyzing LTI systems and filtering signals.
Takeaways
- 📚 The Fourier series is named after Jean-Baptiste Joseph Fourier, a French mathematician and physicist who contributed to the study of trigonometric series and heat equation.
- 🌟 The idea of decomposing a periodic function into simpler oscillating functions dates back to the 3rd century BC, inspired by ancient astronomers' models of planetary motion.
- 🚀 In the mid-1960s, the Fast Fourier Transform (FFT) was developed, increasing the speed of Fourier analysis by over 100 times, which was a significant breakthrough for signal processing.
- 🔄 The Fourier Transform allows for the conversion of a function from the time domain to the frequency domain, enabling the analysis of various frequency components within a signal.
- 📈 The Fourier Transform is widely used in signal processing, communication, and sound analysis, among other fields, as it simplifies the analysis of underlying patterns in signals.
- 🔢 The Fourier Transform can represent any periodic function as a superposition of sine waves with different amplitudes and frequencies.
- 📊 The Fourier Transform of a time-domain signal results in a complex number output, which corresponds to the strength of a given frequency in the original signal.
- 🛠️ The Fourier Transform is particularly useful in analyzing signals from real-world phenomena like electromagnetic waves, voltage across a resistor, and changes in air pressure.
- 🔧 In electronic engineering, the Fourier Transform is used to model linear circuits with components like capacitors, inductors, and resistors, and to understand how systems react to different frequency signals.
- 🔄 The Fourier Transform encapsulates the idea of winding a graph in a cycle with a specific frequency and tracking its center of mass by dividing the number of sampled points.
- 📉 The presentation concludes by emphasizing the importance of the Fourier Transform in LTI System Theory, filtering, and signal processing, highlighting its applications in analyzing complex signals.
Q & A
What is the Fourier series named in honor of?
-The Fourier series is named in honor of Jean-Baptiste Joseph Fourier, a French mathematician and physicist who made significant contributions to the study of trigonometric series and introduced the series to solve the heat equation in metal plates.
What was the purpose of Fourier introducing the series in his 1807 paper?
-Fourier introduced the series in his 1807 paper for the purpose of solving the heat equation in metal plates.
How does the idea of decomposing a periodic function into simple oscillating functions relate to ancient astronomy?
-The idea of decomposing a periodic function into simple oscillating functions dates back to the 3rd century BC when ancient astronomers proposed empirical models of planetary motion based on differences in epicycles, which inspired Fourier's ideas.
What is the significance of the fast Fourier transform (FFT) in the mid-1960s?
-The development of the fast Fourier transform in the mid-1960s increased the speed of Fourier analysis by more than 100 times, enabling electronic computers to perform effective signal analysis and laying the foundation for modern signal processing, telecommunication, data analysis, and scientific research.
What does the Fourier transform do to a signal?
-The Fourier transform converts a signal from the time domain to the frequency domain, allowing us to analyze various frequency components within the signal.
How does the Fourier transform simplify the analysis of complex signals?
-The Fourier transform simplifies the analysis of complex signals by representing them in the frequency domain, making it easier to understand the underlying patterns and frequency content.
What are some examples of real-world signals that can be analyzed using the Fourier transform?
-Examples of real-world signals that can be analyzed using the Fourier transform include electromagnetic waves, voltage across a resistor over time, and changes in air pressure due to speaking.
How does the Fourier transform relate to electronic circuits?
-Every electronic circuit, which includes components such as capacitors, inductors, and resistors, can be modeled at an advanced level using mathematical equations. The Fourier transform helps in understanding how these circuits react to various input signals by analyzing the output in the frequency domain.
What is the concept behind the Fourier transform of a time-domain signal?
-The concept behind the Fourier transform of a time-domain signal is to represent the signal as an infinite sum of sinusoids at every possible frequency, where the output is the sum of the responses for each frequency component.
How is the Fourier transform used in the context of linear time-invariant (LTI) systems?
-The Fourier transform is used in LTI system theory to analyze the system's response to input signals. It simplifies the impact of LTI systems by showing how they react to each frequency component of the input signal.
What is the output of the Fourier transform of an intensity scale function?
-The output of the Fourier transform of an intensity scale function is a complex number, which corresponds to the strength of a given frequency in the original signal.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

工程數學(一)期末報告 Group 5

What is Continuous Wavelet Transform (CWT)? | Wavelet Theory | Advanced Digital Signal Processing

Introduction to Fourier Transform CTFT/FT (Continuous Time Fourier Transform)

Relation between Laplace transform, Fourier transform, z-transform, DTFT, DFT and FFT
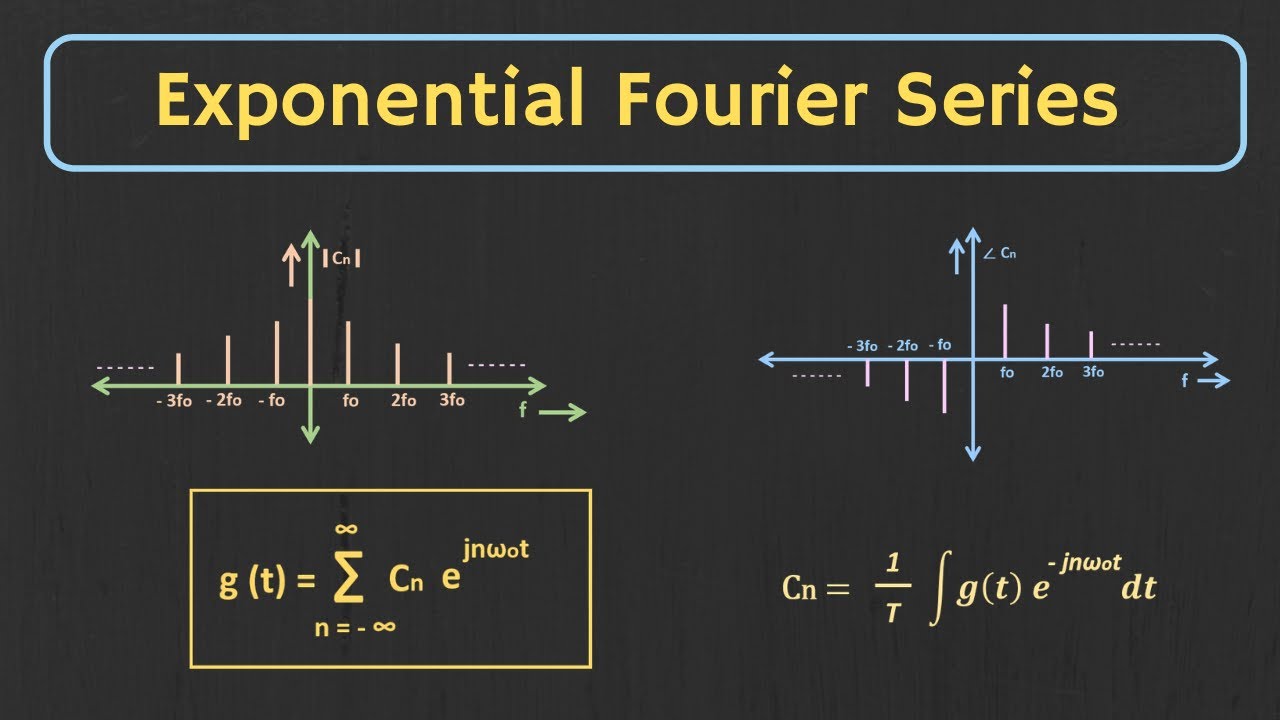
Exponential Fourier Series Explained | Concept of Negative Frequency Explained
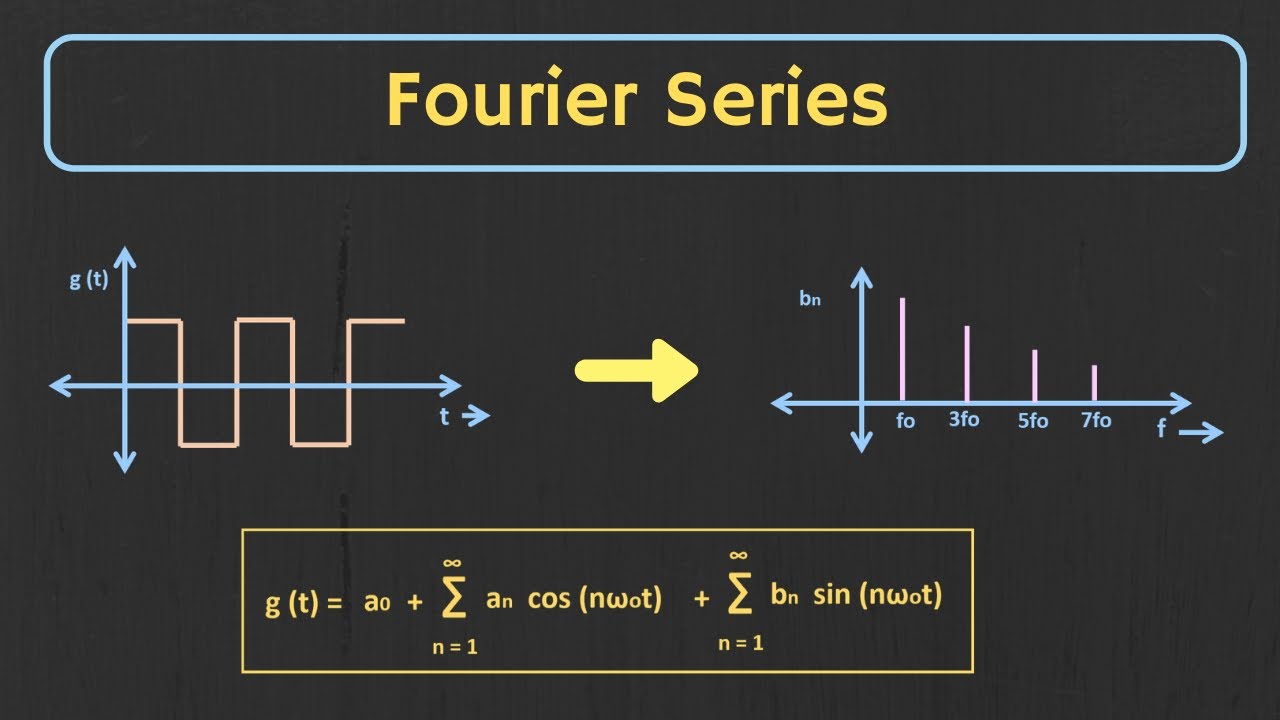
Introduction to Fourier Series | Trigonometric Fourier Series Explained
5.0 / 5 (0 votes)
