20 Kiểm định T tests

Summary

In this script, the focus is on statistical comparison techniques, specifically t-tests. It starts by discussing a basic one-sample t-test, using the example of sales data over five years to check if current sales differ from historical averages. The importance of concepts like degrees of freedom, the t-statistic, and p-values in hypothesis testing is explained. The script also introduces the use of Excel for calculations and the significance of comparing current data to established benchmarks. The key takeaway is the demonstration of how statistical tests can validate if observed differences are meaningful.

Takeaways

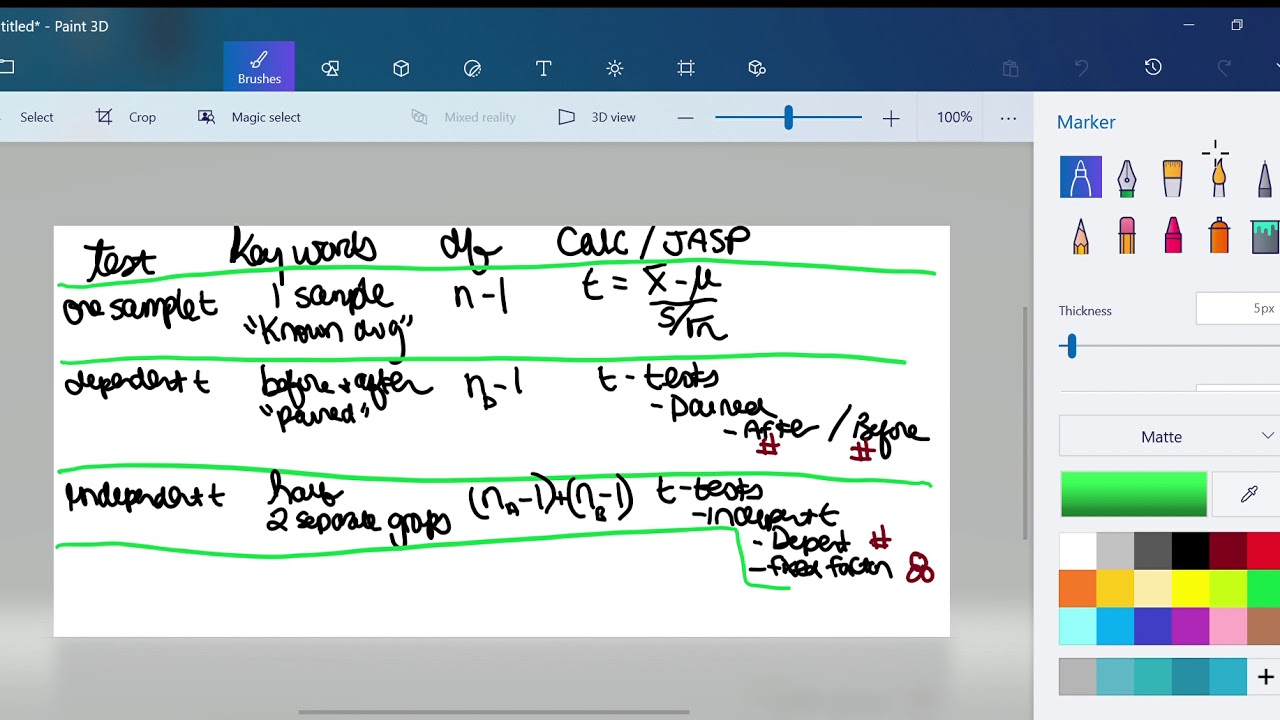
• 😀 One-sample t-test is used to compare a sample's mean to a known population mean.
• 😀 The process of conducting a one-sample t-test involves calculating the sample mean and dividing it by the standard error.
• 😀 Degrees of freedom are essential in determining the significance of statistical results and are linked to the sample size.
• 😀 A t-statistic is calculated to determine if the observed result is statistically significant.
• 😀 The p-value is crucial in hypothesis testing, with values less than 0.05 generally indicating statistical significance.
• 😀 When comparing sales data for Lucy, the aim is to test whether this year's sales differ from the historical average.
• 😀 The concept of statistical hypothesis testing involves determining whether observed differences are significant or due to chance.
• 😀 Z-tests are used when known data, such as standard deviation, is available, particularly for comparisons of two samples.
• 😀 A p-value of 0.02 means there is a 2% chance that the result could be due to random variation, making it statistically significant.
• 😀 If the p-value is less than 0.05, the result is considered statistically significant, indicating a real difference in the data.
• 😀 The goal is to understand if recent data shows significant changes compared to historical data, using methods like t-tests and Z-tests.

Q & A

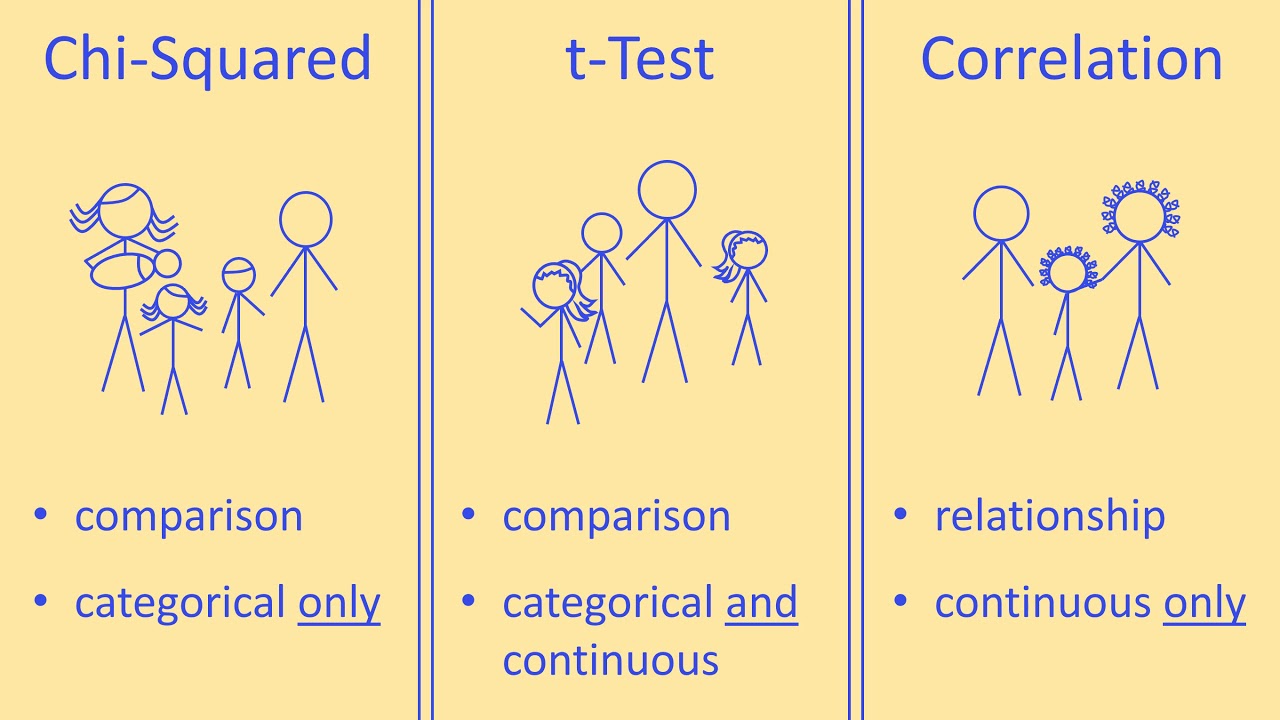
What is a one-sample t-test?

A one-sample t-test is a statistical test used to determine if the mean of a sample differs significantly from a known population mean. It compares the sample's mean with the population mean and tests whether the difference is statistically significant.

What role does the degrees of freedom play in a t-test?

Degrees of freedom (df) refer to the number of independent values in the data that can vary without changing the sample mean. It is crucial in determining the critical value from the t-distribution, which helps assess whether the t-statistic is statistically significant.

How do you calculate the t-statistic in a one-sample t-test?

The t-statistic is calculated by subtracting the population mean from the sample mean, then dividing the result by the standard error. The formula is: t = (sample mean - population mean) / standard error.

What is the p-value, and how is it interpreted in hypothesis testing?

The p-value represents the probability of observing the sample result if the null hypothesis (no difference) is true. A p-value less than 0.05 is commonly considered statistically significant, suggesting that the observed difference is unlikely to be due to random chance.

Why is the one-sample t-test appropriate when comparing Lucy's current sales to historical sales data?

The one-sample t-test is appropriate because we are comparing a sample (current sales) to a known population mean (historical sales). It helps determine if the current sales differ significantly from the historical average.

What does it mean if the p-value is smaller than 0.05 in this context?

If the p-value is smaller than 0.05, it indicates that the difference between Lucy's current sales and her historical sales is statistically significant, meaning it is unlikely to have occurred by chance.

What is the standard error, and how is it calculated?

The standard error measures the variability of the sample mean. It is calculated by dividing the sample's standard deviation by the square root of the sample size. It helps to quantify the uncertainty around the sample mean.

How does the t-distribution relate to the one-sample t-test?

The t-distribution is used to determine the probability of obtaining a t-statistic at least as extreme as the one calculated from the data. The degrees of freedom are used to find the critical values from the t-distribution, which are compared to the computed t-statistic.

What is the significance of the degrees of freedom in determining statistical significance?

The degrees of freedom influence the shape of the t-distribution, and thus, the critical value used to determine statistical significance. More degrees of freedom typically lead to a t-distribution that is closer to the normal distribution.

How can you apply these statistical concepts using Excel?

Excel provides built-in functions for performing a one-sample t-test, calculating the t-statistic, p-value, and degrees of freedom. You can input your sample data and population mean, and Excel will automatically compute the necessary values for the test.