KALKULUS | APLIKASI INTEGRAL | VOLUME BENDA PUTAR
Summary
TLDRيتناول هذا الفيديو شرحًا لطرق حساب حجم الأجسام الدوارة باستخدام التكاملات، مع التركيز على طريقتين: طريقة القرص وطريقة الحلقة. في طريقة القرص، يتم حساب حجم الجسم من خلال تكامل المساحات المقطوعة على طول محور x. أما في طريقة الحلقة، يتم حساب الحجم بطرح حجم الأجسام الداخلية من الأجسام الخارجية. يتم تقديم أمثلة تطبيقية توضح كيفية حساب الحجم باستخدام كل من الطريقتين، بما في ذلك حالات محددة باستخدام دوال معطاة، مما يوفر فهمًا عميقًا لكيفية تطبيق هذه المفاهيم في الرياضيات.
Takeaways
- 😀 يتم استخدام تطبيقات التكامل لحساب حجم الأجسام الدوارة.
- 😀 هناك طريقتان رئيسيتان لحساب حجم الأجسام الدوارة: طريقة الأقراص وطريقة الحلقات.
- 😀 في طريقة الأقراص، يتم حساب الحجم باستخدام منطقة مقطوعة عموديًا تكون على شكل قرص، مع نصف قطره هو قيمة الدالة في نقطة معينة.
- 😀 حجم القرص يتم حسابه باستخدام صيغة πr^2 · Δx حيث r هو نصف القطر و Δx هو سمك القرص.
- 😀 يتم الحصول على الحجم الفعلي عن طريق أخذ حد التكامل عندما يكون عدد التقسيمات لا نهائيًا.
- 😀 في طريقة الحلقات، يتم حساب الحجم عن طريق حساب الفرق بين حجم الجسم الخارجي والداخلي، الذي يحتوي على فراغ في المنتصف.
- 😀 في طريقة الحلقات، يتم استخدام صيغة π(R1^2 - R2^2) حيث R1 هو نصف قطر الجسم الخارجي و R2 هو نصف قطر الجسم الداخلي.
- 😀 في المثال الأول، تم حساب حجم جسم دوار باستخدام طريقة الأقراص على دالة y = x^2، وتم الحصول على حجم قدره 32/5 وحدة مكعبة.
- 😀 في المثال الثاني، تم حساب حجم جسم دوار باستخدام طريقة الأقراص مع دالة y = x^2 والحدود y = 4، وتم الحصول على حجم قدره 8π.
- 😀 في المثال الثالث، تم استخدام طريقة الحلقات لحساب حجم جسم دوار تم تحديده بواسطة y = x^2 وحد y = 4، وكانت النتيجة النهائية 128π/5 وحدة مكعبة.
Q & A
ما هو الهدف من استخدام تطبيقات التكامل في هذه الفيديو؟
-الهدف هو حساب حجم الأجسام الدوارة باستخدام طريقتين: طريقة الأقراص وطريقة الحلقات.
كيف يتم حساب حجم الجسم الناتج عن تدوير المنطقة المحصورة تحت دالة حول المحور السيني؟
-يتم حساب الحجم باستخدام طريقة الأقراص حيث يتم حساب حجم كل قرص على حدة باستخدام الصيغة π * (f(x))² * Δx ومن ثم تكاملها من a إلى b.
ما هي الصيغة التي يتم استخدامها لحساب حجم الجسم الناتج عن تدوير المنطقة المحصورة تحت دالة حول المحور السيني؟
-الصيغة هي: V = π ∫[a, b] (f(x))² dx.
ماذا يحدث عند زيادة عدد التقسيمات (n) إلى ما لا نهاية في طريقة الأقراص؟
-عند زيادة عدد التقسيمات إلى ما لا نهاية، يتم الحصول على الحجم الفعلي للجسم عن طريق أخذ الحد الأقصى للتكامل.
كيف يمكن حساب حجم الجسم الناتج عن تدوير المنطقة المحصورة بين منحنى ودالة معينة حول المحور الصادي؟
-يتم حساب الحجم باستخدام طريقة الأقراص الأفقية حيث يتم تكامل معبرًا عن المسافة بين المنحنى ومحور y، وبالتالي يتم استخدام الصيغة π ∫[a, b] (g(y))² dy.
ما هي المعادلة التي تم استخدامها لحساب حجم الجسم الناتج عن تدوير المنطقة المحصورة تحت منحنى y = x² حول المحور السيني؟
-تم استخدام المعادلة: V = π ∫[0, 2] (x²)² dx.
ما هي طريقة الحلقات المستخدمة لحساب حجم الجسم الدوار؟
-طريقة الحلقات تستخدم لإيجاد حجم الأجسام الدوارة التي تحتوي على فراغ داخلي، حيث يتم حساب حجم الجسم الخارجي وطرح حجم الجسم الداخلي.
كيف يتم تطبيق طريقة الحلقات لحساب حجم الجسم الناتج عن تدوير المنطقة بين المنحنيين y = x² و y = 4 حول المحور السيني؟
-يتم حساب الحجم باستخدام طريقة الحلقات عن طريق تكامل المسافة بين المنحنى العلوي (y = 4) والمنحنى السفلي (y = x²) عبر الصيغة π ∫[0, 2] (4 - x²)² dx.
ما هو الحل النهائي لحساب حجم الجسم الناتج عن تدوير المنطقة المحصورة بين المنحنى y = x² والخط y = 4 حول المحور السيني باستخدام طريقة الحلقات؟
-الحل النهائي هو 128/5 π، وهو الحجم الناتج بعد إجراء التكامل.
ما هي الفائدة الرئيسية من استخدام طريقة الحلقات مقارنة بطريقة الأقراص؟
-الفائدة الرئيسية هي أن طريقة الحلقات تستخدم عندما يكون هناك فراغ داخلي في الجسم الدوار، مما يسمح بحساب الحجم الكلي للمنطقة الخارجية وطرح الحجم الداخلي.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Contrôle 1 Semestre 1 SVT 1ère Bac SX : Réaliser la Carte Paléogéographique d'une Région

Calculus 1 Review - Basic Introduction

كيفيه عمل اعاقه الكابلري للمكيف اعاقه غاز 22

Binomial Distribution EXPLAINED with Examples

Pressione in Fisica - Definizione & Spiegazione

NES470- Network Management - Chapter 4 - slides 1- 8
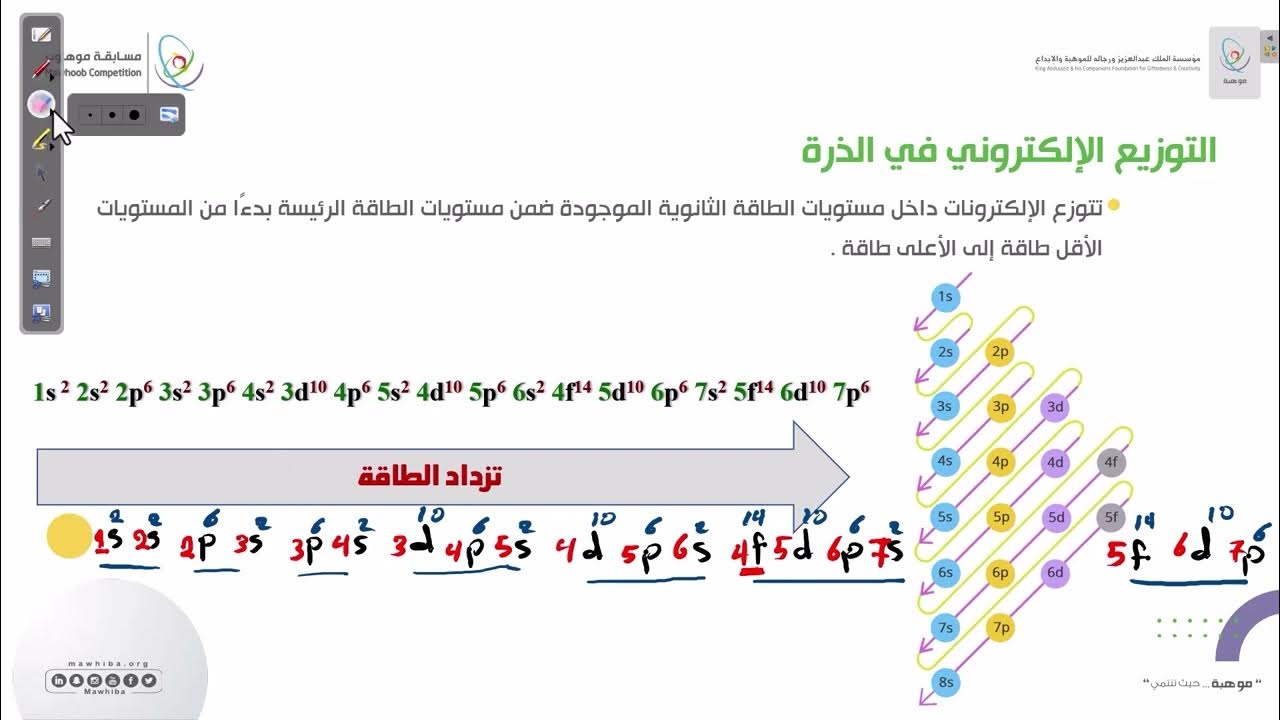
مسابقة موهوب 2 - (الكيمياء): التوزيع الإلكتروني في الذرة 2
5.0 / 5 (0 votes)
