Derivada de un cociente | Ejemplo 3 | Regla de la cadena
Summary
TLDREn este video, se explica detalladamente cómo calcular la derivada de un cociente usando la regla del cociente. Se cubren aspectos clave como la aplicación de la regla de la cadena, la derivación de expresiones con exponentes, la simplificación de términos, y la factorización de los resultados obtenidos. A lo largo del proceso, el instructor guía paso a paso, destacando la importancia de la organización y la correcta aplicación de las fórmulas. Al final, se invita a los estudiantes a practicar y a suscribirse al canal para continuar aprendiendo sobre el tema.
Takeaways
- 😀 El video explica cómo calcular la derivada de una función racional utilizando la regla del cociente.
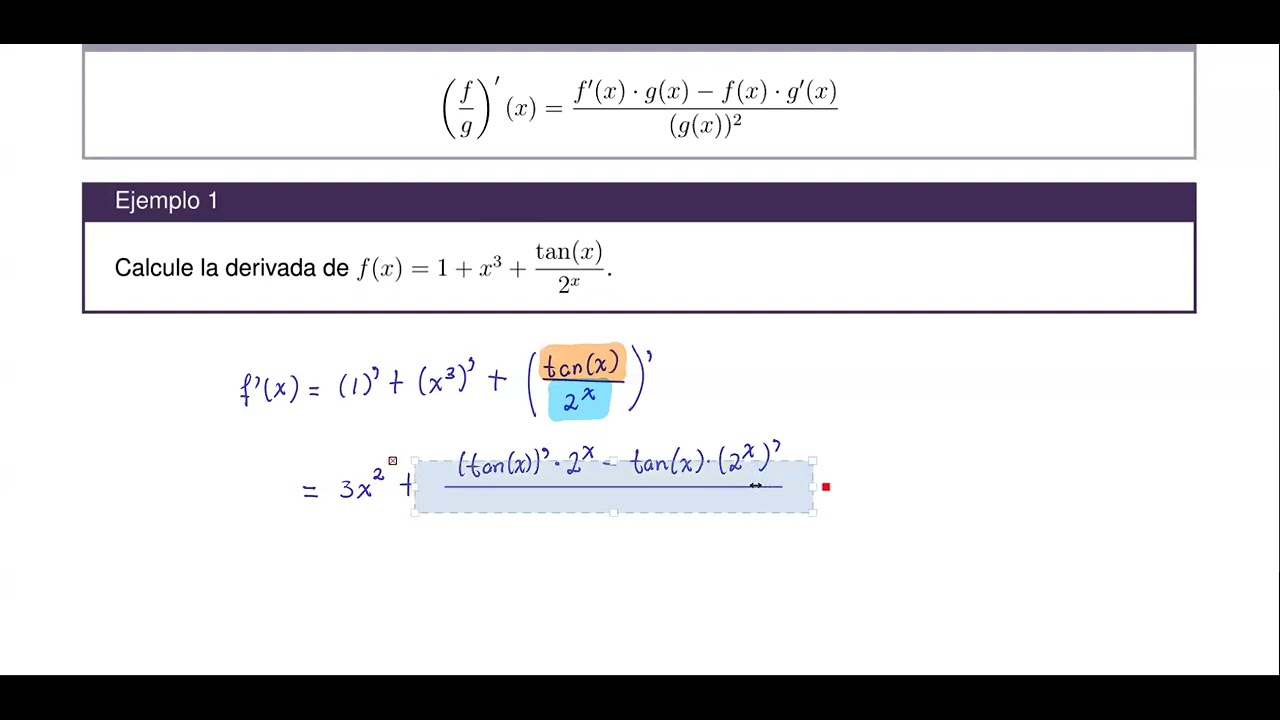
- 😀 La regla del cociente se aplica multiplicando el denominador por la derivada del numerador, restando el numerador por la derivada del denominador, y dividiendo entre el denominador elevado al cuadrado.
- 😀 Es importante seguir el orden correcto de las operaciones para evitar errores en los signos de los términos.
- 😀 Se debe derivar primero el exponente y luego la parte interna de la expresión utilizando la regla de la cadena.
- 😀 La derivada de una constante es 0, lo cual simplifica los términos en algunos casos.
- 😀 En la derivada de un cociente, los términos deben ser escritos de forma clara y ordenada para evitar confusiones en los cálculos.
- 😀 Al factorizar, se debe identificar y extraer los factores comunes, ya sean números o términos algebraicos.
- 😀 La simplificación de expresiones es esencial para reducir la complejidad del resultado final, como eliminar términos comunes o aplicar la propiedad de los exponentes.
- 😀 En ocasiones, se recomienda reordenar los términos antes de factorizar para facilitar el proceso de simplificación.
- 😀 El profesor sugiere que los estudiantes practiquen con ejercicios adicionales para afianzar los conceptos y mejorar en el manejo de derivadas y simplificación de expresiones.
Q & A
¿Qué es la regla del cociente en derivadas?
-La regla del cociente se utiliza para derivar funciones que son el cociente de dos expresiones. La fórmula es: la derivada de un cociente es igual a (el denominador por la derivada del numerador menos el numerador por la derivada del denominador), todo dividido entre el denominador al cuadrado.
¿Qué se debe hacer al derivar una expresión con exponente?
-Cuando se deriva una expresión con exponente, se debe aplicar la regla de la cadena. Primero, se baja el exponente y se le resta 1, luego se multiplica por la derivada de lo que está dentro del paréntesis.
¿Cómo se simplifican las expresiones al aplicar la regla del cociente?
-Se simplifican al identificar factores comunes en el numerador y denominador, como el término '4x - 3' en varios factores. Se aplican operaciones de multiplicación y división entre los factores, eliminando términos semejantes.
¿Qué errores deben evitarse al usar la regla del cociente?
-Uno de los errores más comunes es cambiar el orden en la fórmula, como comenzar con la derivada del numerador por el denominador en lugar de al revés. Esto cambiaría los signos y haría el resultado incorrecto.
¿Por qué es importante factorizar cuando se trabaja con derivadas de cocientes?
-Factorizar ayuda a simplificar las expresiones y facilita la cancelación de términos comunes, lo que hace que el cálculo sea más fácil y menos propenso a errores.
¿Cómo se realiza la derivada del denominador en el ejercicio mostrado?
-Se aplica la misma regla de la cadena. Se baja el exponente del denominador, se multiplica por la derivada de lo que está dentro del paréntesis y se simplifican los resultados.
¿Cuáles son los pasos clave para derivar una función de cociente?
-Los pasos son: 1) Identificar el numerador y denominador. 2) Derivar el numerador y el denominador por separado. 3) Aplicar la fórmula de la derivada del cociente: (denominador * derivada del numerador - numerador * derivada del denominador) / denominador².
¿Qué significa 'factorizar por factor común' en el contexto de derivadas?
-Significa identificar y extraer términos comunes en los factores del numerador y el denominador, como '4x - 3'. Esta técnica simplifica la expresión y facilita el proceso de derivación.
¿Cómo se manejan los términos con exponentes diferentes al aplicar la derivada?
-Cuando los términos tienen exponentes diferentes, no se pueden simplificar directamente. En su lugar, se deben restar los exponentes para obtener el exponente final después de simplificar los factores comunes.
¿Cuándo se debe utilizar la propiedad de la potenciación al derivar?
-La propiedad de la potenciación se utiliza cuando hay un término con base elevada a un exponente. En este caso, se deben multiplicar los exponentes si se está aplicando una operación entre bases con exponentes.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)