1 An introduction to vectors

Summary

This video introduces the concept of vectors, explaining their difference from scalars. Scalars have only magnitude, while vectors have both magnitude and direction. The script covers vector representation using directed line segments, component form with i and j notation, and methods for calculating vector magnitudes and directions. The use of trigonometry to resolve vector components and find angles is demonstrated. Practical examples, including converting vectors to column and i-j notation, are provided, alongside exercises to reinforce understanding. The session aims to establish foundational vector knowledge for further study and application.

Takeaways

• 😀 Vectors are quantities that have both magnitude (size) and direction, unlike scalars which only have magnitude.
• 😀 Distance is a scalar quantity, whereas displacement is a vector that includes both magnitude (distance) and direction.
• 😀 Vectors are represented by directed line segments, with arrows indicating the direction of motion.
• 😀 When writing vectors, small lowercase letters are used, with an underscore (e.g., 'a') or bold letters to represent vectors in printed form.
• 😀 Component form of vectors uses 'i' and 'j' notation, where 'i' represents the x-direction and 'j' represents the y-direction.
• 😀 Vectors can be written in column vector notation (e.g., [3, 2]) or in i-j notation (e.g., 3i + 2j).
• 😀 The magnitude (size) of a vector is calculated using the Pythagorean theorem and is always a positive scalar.
• 😀 Magnitude is denoted with modulus signs, e.g., |a|, and is calculated as √(x² + y²) for a vector with components (x, y).
• 😀 The direction of a vector is often expressed as an angle, measured counterclockwise from the positive horizontal axis.
• 😀 To find the angle of a vector, trigonometry is used, typically involving tangent (opposite/adjacent) and adjusting for direction as needed.
• 😀 When given magnitude and angle, you can calculate the vector components using trigonometric functions like sine and cosine.

Q & A

What is the difference between a vector and a scalar?

A scalar is a quantity that only has magnitude (size), such as distance. A vector, however, has both magnitude and direction, such as displacement, which specifies not only how far you travel but also the direction of travel.

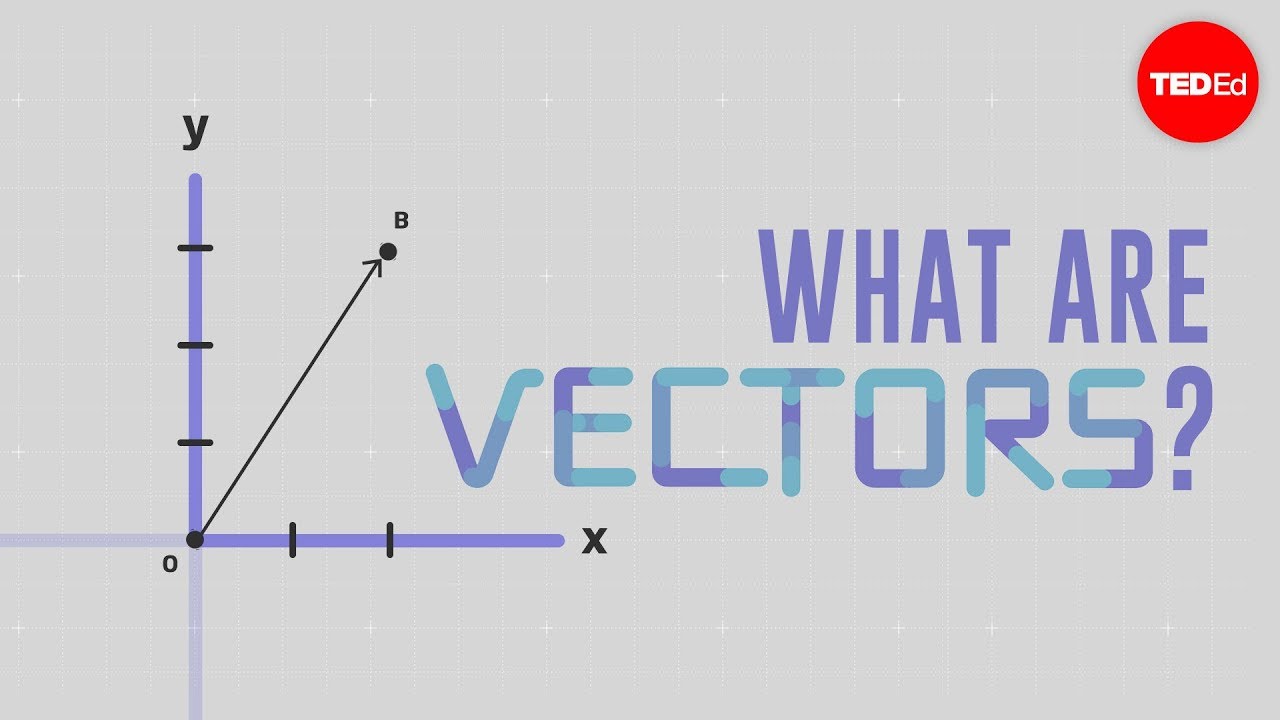
How is a vector represented geometrically?

A vector is represented by a directed line segment, which is a straight line with an arrow showing the direction of travel. The starting point is usually labeled as the origin (O), and the endpoint is labeled as the point (P).

What is the significance of the arrow on a vector?

The arrow on a vector indicates the direction in which the vector points. For example, in the vector from O to P, the arrow shows the direction from the origin to the point P.

How do you denote a vector using notation?

Vectors are denoted with a small letter, often in bold, or with a line underneath the letter (e.g., **a** or a with an underscore). This shows that the letter represents a vector, not just a scalar quantity.

What is component form of a vector, and how is it written using i and j notation?

Component form expresses a vector in terms of its horizontal (x) and vertical (y) components using unit vectors i (in the x direction) and j (in the y direction). For example, a vector with 3 units in the x direction and 2 units in the y direction can be written as 3i + 2j.

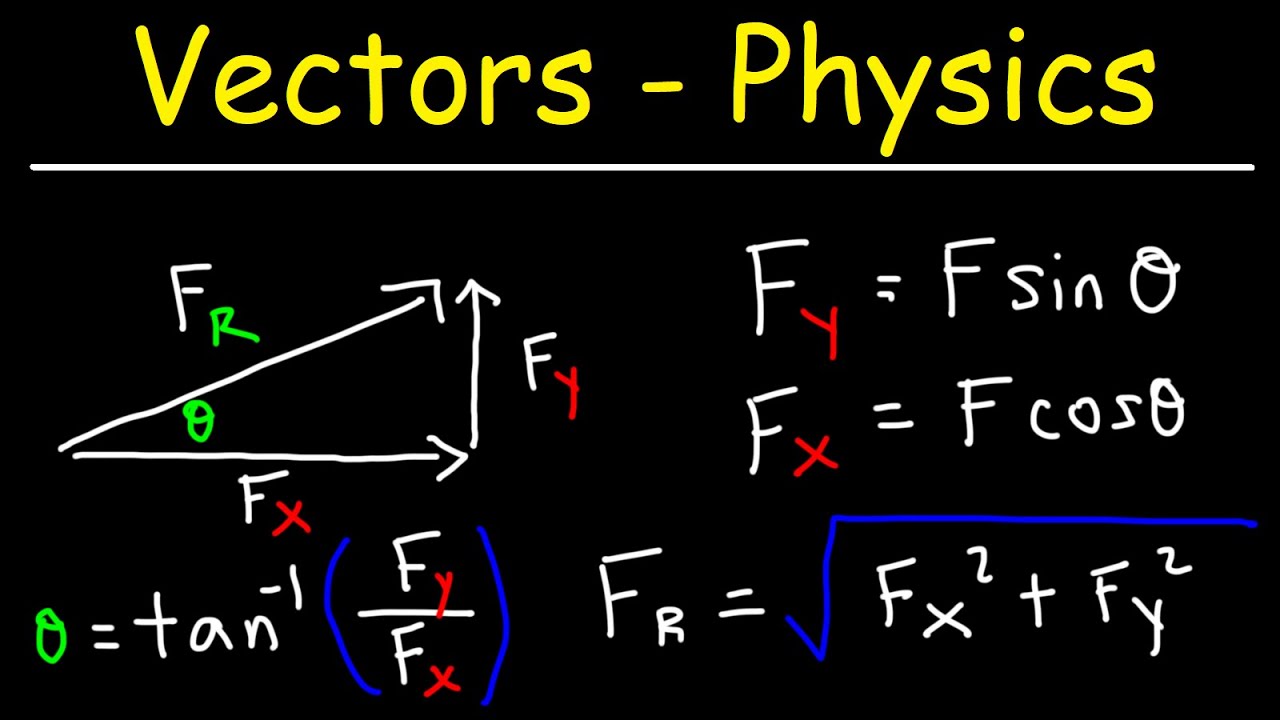
How do you calculate the magnitude of a vector?

The magnitude of a vector can be calculated using Pythagoras' theorem. If the vector has components (x, y), the magnitude is √(x² + y²). For example, for the vector 3i + 2j, the magnitude would be √(3² + 2²) = √13.

What is the modulus of a vector, and how is it related to the magnitude?

The modulus of a vector is the same as its magnitude, which is the length of the vector. The magnitude is always a positive scalar quantity, regardless of the vector's direction.

How do you determine the direction of a vector?

The direction of a vector can be determined by calculating the angle it makes with the positive horizontal axis. This angle can be found using trigonometry, specifically the inverse tangent function (tan⁻¹). The angle is measured counterclockwise from the positive horizontal axis.

What is the process to calculate the angle of a vector from the horizontal axis?

To calculate the angle, you use the tangent function. The angle θ is found by tan⁻¹(opposite/adjacent). For example, for the vector 3i + 2j, the angle is tan⁻¹(2/3), which is approximately 33.7 degrees.

How can we find the components of a vector if its magnitude and angle are given?

If you know the magnitude and the angle of a vector, you can find its components using trigonometry. For example, if the vector has magnitude 10 and angle 30 degrees, you can use cosine and sine: x = magnitude * cos(angle) and y = magnitude * sin(angle). For this example, x = 10 * cos(30) = 5, and y = 10 * sin(30) = 5√3.