Big-O Notation in 3 Minutes
Summary
TLDRThis video explains Big O notation and its importance in understanding algorithm efficiency. It covers various time complexities from constant time to factorial time, with examples like binary search, sorting algorithms, and matrix multiplication. The video emphasizes that while Big O is a useful starting point, real-world performance can be influenced by factors like caching and hardware. It provides practical insights, such as the advantages of traversing arrays row by row for better cache performance and why arrays generally outperform linked lists in linear traversal.
Takeaways
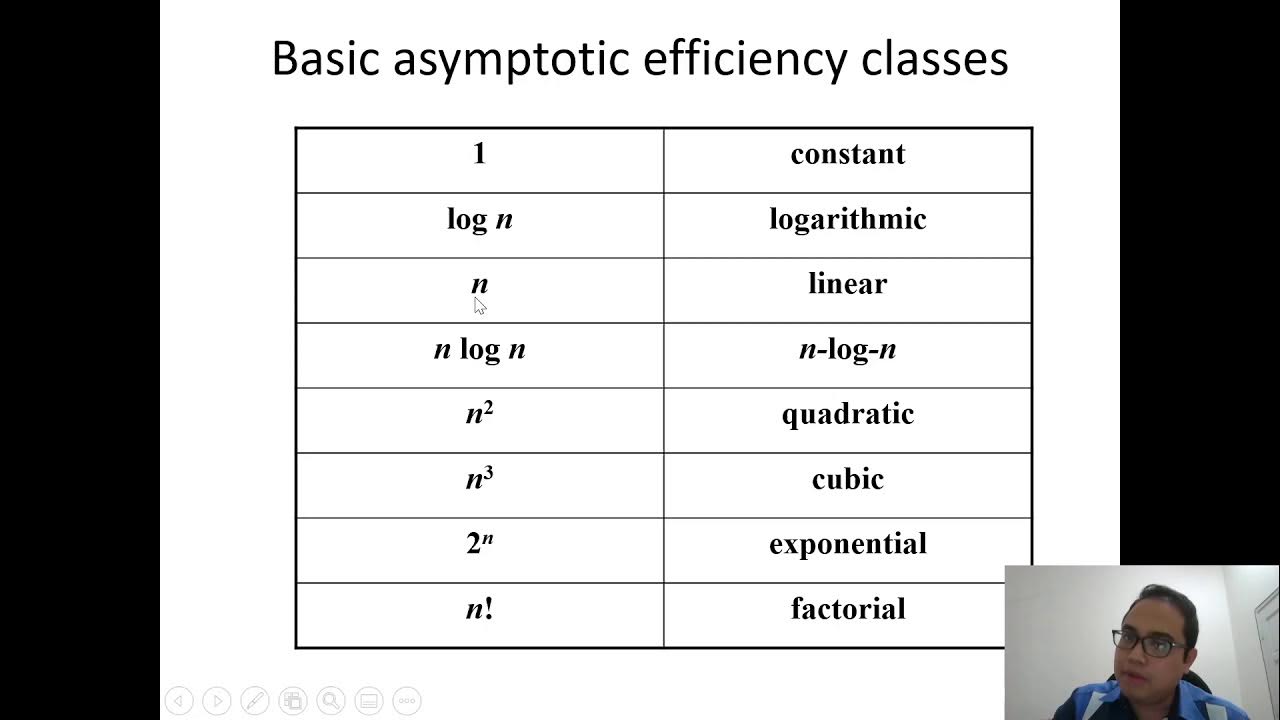
- 😀 Big O notation measures how runtime scales with input size, and is essential for understanding algorithm efficiency.
- 😀 Constant time (O(1)) means the runtime stays the same regardless of input size, such as array indexing or hashtable operations.
- 😀 Logarithmic time (O(log n)) grows slowly as input increases, with binary search as a classic example.
- 😀 Linear time (O(n)) grows directly with input size, such as when finding the maximum value in an unsorted array.
- 😀 Log-linear time (O(n log n)) is efficient for sorting algorithms like merge sort, quicksort, and heap sort.
- 😀 Quadratic time (O(n^2)) grows with the square of input size, often seen in basic sorting algorithms like bubble sort, especially with nested loops.
- 😀 Cubic time (O(n^3)) grows with the cube of input size, commonly seen in algorithms with three nested loops, such as naive matrix multiplication.
- 😀 Exponential time (O(2^n)) doubles with each additional input, which is typical in some recursive algorithms and grows impractically fast for large inputs.
- 😀 Factorial time (O(n!)) grows extremely fast and is associated with algorithms that generate all possible permutations, making it impractical for larger inputs.
- 😀 Real-world performance may differ from Big O estimates due to factors like caching, memory usage, and hardware specifications, which can sometimes outweigh algorithmic complexity.
- 😀 Optimization strategies should go beyond Big O; profiling your code and understanding hardware-specific factors like cache locality can significantly improve performance.
Q & A
What is Big O notation and why is it important?
-Big O notation is a mathematical notation used to describe the performance or complexity of an algorithm in terms of its time or space requirements as a function of input size. It is important because it helps to understand how an algorithm will scale with larger inputs, allowing developers to optimize code for performance.
What does O(1) mean in Big O notation?
-O(1) represents constant time complexity, meaning that the runtime of an algorithm does not change with the size of the input. Operations like array indexing or hash table lookups typically have constant time complexity.
Can you explain the difference between O(log n) and O(n)?
-O(log n) denotes logarithmic time complexity, where the runtime grows slowly as input size increases (e.g., binary search). O(n) indicates linear time complexity, where runtime grows directly in proportion to the input size (e.g., traversing an unsorted array). O(log n) is much more efficient for large data sets compared to O(n).
What are the practical use cases for O(n log n) time complexity?
-O(n log n) is commonly seen in efficient sorting algorithms like merge sort, quicksort, and heap sort. These algorithms balance the need to divide the problem into smaller chunks (log n) while processing each element (n), making them optimal for comparison-based sorting tasks.
What are some examples of algorithms with O(n²) time complexity?
-Algorithms with O(n²) time complexity include bubble sort, insertion sort, and selection sort. These algorithms often involve nested loops iterating over the same data, resulting in a quadratic growth in runtime as the input size increases.
Why is O(n³) often associated with cubic time complexity?
-O(n³) represents cubic time complexity, where runtime grows with the cube of the input size. This is typically seen in algorithms that involve three nested loops, such as naive matrix multiplication, where each element is processed multiple times in a cubic fashion.
How does O(2ⁿ) exponential time complexity impact performance?
-O(2ⁿ) denotes exponential time complexity, where runtime doubles with each additional input element. This type of complexity is common in recursive algorithms, such as certain backtracking problems, and becomes impractical very quickly for larger input sizes.
What kind of algorithms have O(n!) factorial time complexity?
-O(n!) represents factorial time complexity, where runtime grows extremely fast as input size increases. This is seen in algorithms that generate all permutations of a set, such as the traveling salesman problem. Factorial time complexity is usually infeasible for larger inputs.
How do caching and memory access affect real-world algorithm performance?
-In real-world scenarios, factors like CPU cache efficiency and memory access patterns can have a significant impact on performance, sometimes more than algorithmic complexity. For example, algorithms that maximize cache hits or optimize memory locality can outperform those with lower Big O complexity in practice.
Why is traversing a 2D array row-wise often faster than column-wise, even though both have O(n²) complexity?
-Although both row-wise and column-wise traversal of a 2D array have O(n²) time complexity, row-wise traversal is typically faster because it benefits from better cache locality. In row-wise traversal, elements are stored contiguously in memory, making sequential access more cache-friendly and reducing memory access latency.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Complete Beginner's Guide to Big O Notation

Time & Space Complexity - Big O Notation - DSA Course in Python Lecture 1
CSC645 - Chapter 1 (Continued) - Fundamentals of Algorithm Analysis

Learn Big O notation in 6 minutes 📈

2 1 The Gist 14 min

Time Complexity | Big O Notation | Data Structures & Algorithms | JomaClass
5.0 / 5 (0 votes)
