Complete Beginner's Guide to Big O Notation

Summary

This video provides an in-depth introduction to Big O notation, a critical concept for analyzing algorithm efficiency. The speaker explains how time complexity helps compare different algorithm implementations and make performance decisions, focusing on common time complexities like O(1), O(n), and O(n²). Using clear examples, the video illustrates how to calculate the number of operations in an algorithm and how Big O notation simplifies performance analysis. Additionally, the speaker briefly touches on space complexity and offers tips for understanding algorithmic trade-offs. The video aims to demystify these concepts for developers and enthusiasts alike.

Takeaways

• 😀 Big O notation helps us evaluate and compare algorithms based on their performance, especially in terms of time complexity.
• 😀 Time complexity is crucial for making decisions about which algorithm to choose, particularly in terms of speed and scalability.
• 😀 Big O notation is a way to describe how an algorithm’s performance scales as the input size (n) grows.
• 😀 In programming, it’s essential to be able to compare different algorithm implementations to understand which is most efficient.
• 😀 Timing algorithms can be unreliable for measuring performance due to variability in results and precision limits in JavaScript.
• 😀 To properly evaluate an algorithm, we focus on the number of operations it performs, not the actual time it takes.
• 😀 Simple algorithms with constant operations, like mathematical formulas, are more efficient (O(1)) compared to those with loops (O(n)).
• 😀 O(n) time complexity implies that the number of operations grows linearly as the input size increases, which is good for performance.
• 😀 O(n^2) time complexity, resulting from nested loops, can quickly become inefficient as n grows larger, and should be avoided when possible.
• 😀 Big O notation simplifies the comparison of algorithms by focusing on the big picture and ignoring constants or smaller terms.
• 😀 Space complexity is a similar concept to time complexity, but it focuses on how much memory an algorithm uses as the input size grows.

Q & A

What is Big O notation and why is it important in algorithm analysis?

Big O notation is a mathematical notation used to describe the performance or complexity of an algorithm in terms of time or space as the input size grows. It is important because it provides a way to compare algorithms based on how efficiently they handle increasing amounts of data.

What does O(1) represent in terms of algorithm performance?

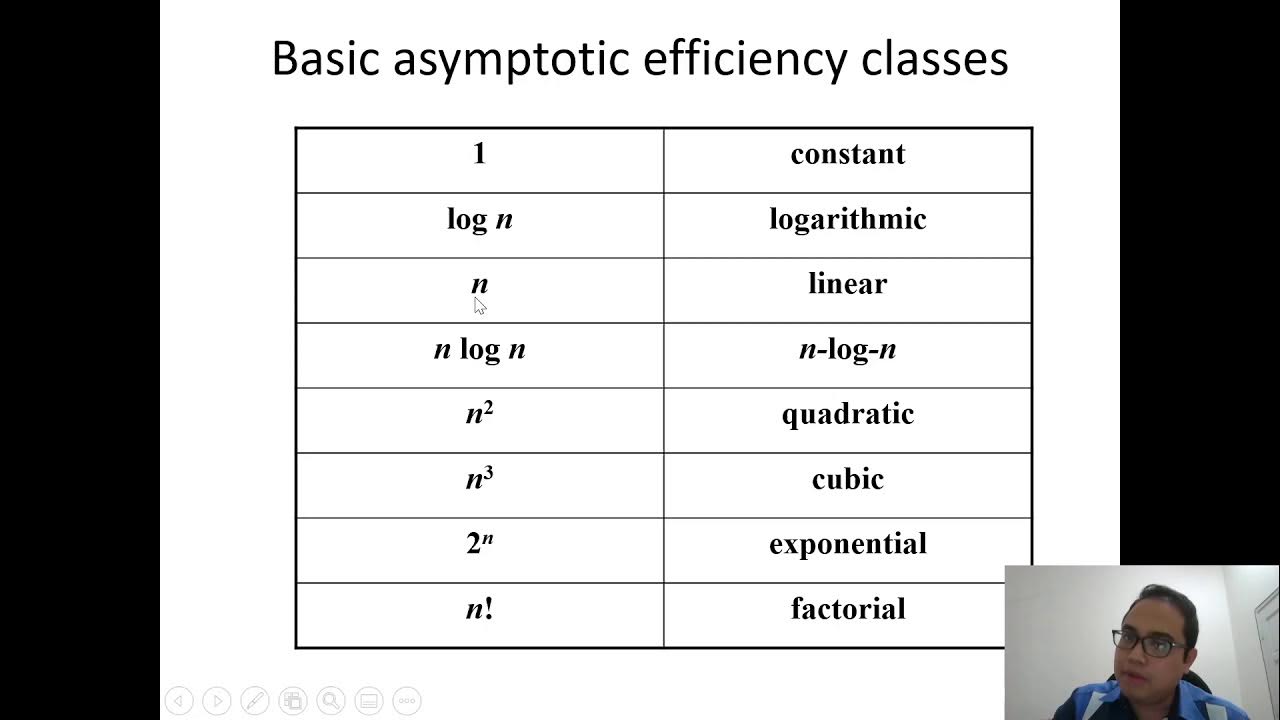
O(1) represents constant time complexity, meaning that the algorithm's performance or execution time does not change with the size of the input. It will always perform the same number of operations, regardless of how large the input is.

How does O(n) differ from O(1)?

O(n) represents linear time complexity, where the execution time grows proportionally with the size of the input. As the input size increases, the algorithm will require more operations, unlike O(1), which always takes the same amount of time.

Why is it misleading to use timers to measure algorithm performance directly?

Timers can be imprecise for very fast operations because they are affected by various external factors such as CPU load and operating system overhead. Big O notation focuses on the number of operations rather than the time it takes to execute them, offering a more reliable measure of performance.

What does O(n²) mean, and when is it typically seen in algorithms?

O(n²) represents quadratic time complexity, where the number of operations grows as the square of the input size. This is typically seen in algorithms that involve nested loops, where each element in the input is compared with every other element.

Can you explain the importance of Big O notation when comparing algorithms?

Big O notation helps identify which algorithm will scale better with larger input sizes. By analyzing the time complexity of different algorithms, developers can choose the most efficient one, ensuring faster execution as data grows, especially in large-scale systems.

What is the relationship between space complexity and Big O notation?

Space complexity, like time complexity, is measured using Big O notation, but it focuses on the amount of memory an algorithm requires as the input size increases. An algorithm with high space complexity may require significant memory, which can be a constraint in resource-limited environments.

Why is it not necessary to write O(5) or O(1000) when discussing Big O notation?

Big O notation simplifies expressions by ignoring constant factors, as they do not affect the overall growth rate of an algorithm. Whether the algorithm takes 5 or 1000 operations is insignificant for large input sizes, so we express it as O(1), indicating constant time regardless of the constant.

What happens when the input size 'n' is less than 5 in the script example?

If n is less than 5, the loop runs a number of times equal to n, meaning the number of iterations is directly proportional to n. However, as n grows larger than 5, the loop will run exactly 5 times, making the performance constant regardless of the input size.

How does Big O notation help in making decisions about which algorithm to use?

Big O notation helps developers make informed decisions about the scalability of algorithms. By understanding the time and space complexities of different algorithms, they can choose the one that will handle large input sizes most efficiently, saving time and resources in production environments.