2 1 The Gist 14 min

Summary

This video script introduces Asymptotic Analysis, a fundamental concept for computer scientists and programmers to discuss algorithm performance. It emphasizes the importance of understanding Big O notation for high-level algorithmic comparisons, especially for large inputs where efficiency is critical. The script provides intuitive examples, such as linear search, to illustrate how Big O notation helps in identifying the growth rate of algorithms, suppressing constant factors and lower-order terms to focus on the dominant behavior.

Takeaways

• 📘 Asymptotic Analysis is a fundamental concept for computer scientists and programmers to discuss high-level performance of algorithms.
• 🔍 It provides a vocabulary to differentiate between algorithmic approaches, especially useful for large inputs where algorithmic ingenuity is crucial.
• 🔑 The main idea of Asymptotic Analysis is to suppress leading constant factors and lower-order terms to focus on the high-level performance.
• 📉 Lower-order terms become less significant as the input size increases, which is why they are often ignored in Asymptotic Analysis.
• 🔢 Constant factors are environment-dependent and can vary with compiler, programming language, and other factors, hence their suppression in the analysis.
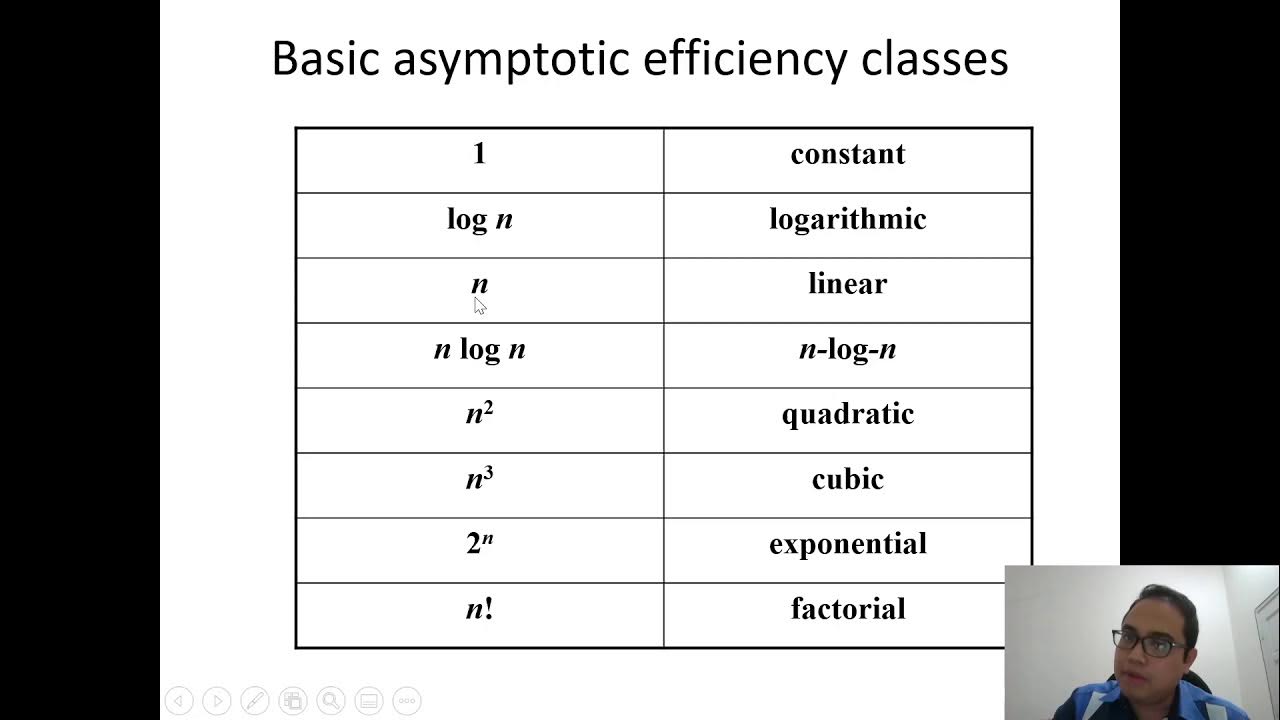
• 🔄 An example given is Merge Sort, where the running time is simplified to O(n log n) by dropping lower-order terms and constant factors.
• 🔍 The 'Big O' notation is used to express the upper bound of an algorithm's running time in terms of input size, ignoring constants and lower-order terms.
• 🔎 The script provides four examples to illustrate different time complexities, including linear (O(n)) and quadratic (O(n^2)) time algorithms.
• 🔄 In the linear search example, the running time is directly proportional to the array length, demonstrating a linear time complexity.
• 🔄🔄 The nested loop example, where each element of one array is compared with every element of another, results in a quadratic time complexity.
• 🔄➡️ The final example modifies the nested loop to search for duplicates within a single array, maintaining the quadratic time complexity but optimizing comparisons.

Q & A

What is Asymptotic Analysis in the context of computer science?

Asymptotic Analysis is a method used to understand the performance of algorithms, especially their growth in time or space requirements as the input size grows. It is crucial for computer programmers and scientists to discuss the high-level performance of computer algorithms.

Why is Asymptotic Analysis important for programmers?

Asymptotic Analysis is important because it provides a common language and framework to discuss and compare the efficiency of different algorithms, particularly in terms of their scalability and performance with large inputs.

What does the term 'Big O' in computer science signify?

The term 'Big O' refers to the notation used in Asymptotic Analysis to describe the upper bound of an algorithm's growth rate. It helps in classifying algorithms according to how their run time or space requirements increase with the size of the input.

How does Asymptotic Analysis help in ignoring irrelevant details?

Asymptotic Analysis helps by focusing on the highest order terms and suppressing constant factors and lower-order terms, which are often irrelevant when considering the performance of algorithms on large inputs or when comparing different algorithmic approaches.

What is the significance of 'n' in the context of Big O notation?

In Big O notation, 'n' typically represents the size of the input to an algorithm. The growth rate of an algorithm's run time or space complexity is expressed in terms of 'n', allowing for a standardized way to compare different algorithms.

Can you provide an example of a linear time algorithm from the script?

An example of a linear time algorithm discussed in the script is a straightforward search through an array for a given integer, where the running time is directly proportional to the length of the array, denoted as O(n).

What is the difference between the running time of a linear time algorithm and a quadratic time algorithm?

A linear time algorithm has a running time that grows linearly with the input size (O(n)), while a quadratic time algorithm's running time grows quadratically (O(n^2)), meaning that doubling the input size results in a fourfold increase in run time for the quadratic algorithm.

How does the script justify the suppression of constant factors in Asymptotic Analysis?

The script justifies the suppression of constant factors by explaining that they are highly dependent on the environment, such as the compiler, programming language, and architecture, and are thus not the focus when comparing high-level algorithmic approaches.

What is the role of lower-order terms in Asymptotic Analysis?

Lower-order terms become increasingly irrelevant as the focus shifts to large inputs, which is where algorithmic ingenuity is most needed. Therefore, they are often suppressed in Asymptotic Analysis to simplify the expression of an algorithm's growth rate.

Can you explain the example of searching for a common number in two arrays as presented in the script?

The script presents an example where two arrays of length n are searched for a common number. The straightforward approach involves a nested loop, comparing each element of the first array with each element of the second array, resulting in a quadratic running time of O(n^2).

What is the purpose of the example involving finding duplicates in a single array?

The purpose of this example is to illustrate how a nested loop can be used to check for duplicate entries in a single array. The running time for this operation is also quadratic (O(n^2)), but the script explains how to optimize the loop to avoid unnecessary comparisons.