Perbandingan trigonometri pada segitiga siku siku, Menjelaskan rasio trigonometri

Summary

This educational video introduces trigonometric ratios in right-angled triangles, starting with the Pythagorean theorem to determine missing sides. It covers basic trigonometric functions like sine, cosine, and tangent, and explores their relationships with angles. The video also highlights special angles (30°, 45°, 60°) and provides practical examples and problems. With clear explanations, the script guides learners through solving problems step-by-step, making complex trigonometric concepts more accessible. The video aims to simplify trigonometry for beginners, encouraging understanding through exercises and real-world applications.

Takeaways

• 😀 Trigonometric ratios like sine, cosine, and tangent are essential for solving problems involving right-angled triangles.
• 😀 The Pythagorean theorem (a² + b² = c²) is used to calculate the unknown side lengths in right triangles.
• 😀 Sine, cosine, and tangent can be defined as ratios of different sides of a right triangle relative to the angles.
• 😀 Special angles such as 30°, 45°, and 60° have specific sine, cosine, and tangent values that are important to remember.
• 😀 Trigonometric functions can be extended to include cosecant, secant, and cotangent by taking reciprocals of sine, cosine, and tangent.
• 😀 Understanding the basic trigonometric relationships is crucial when solving problems involving angles and sides in triangles.
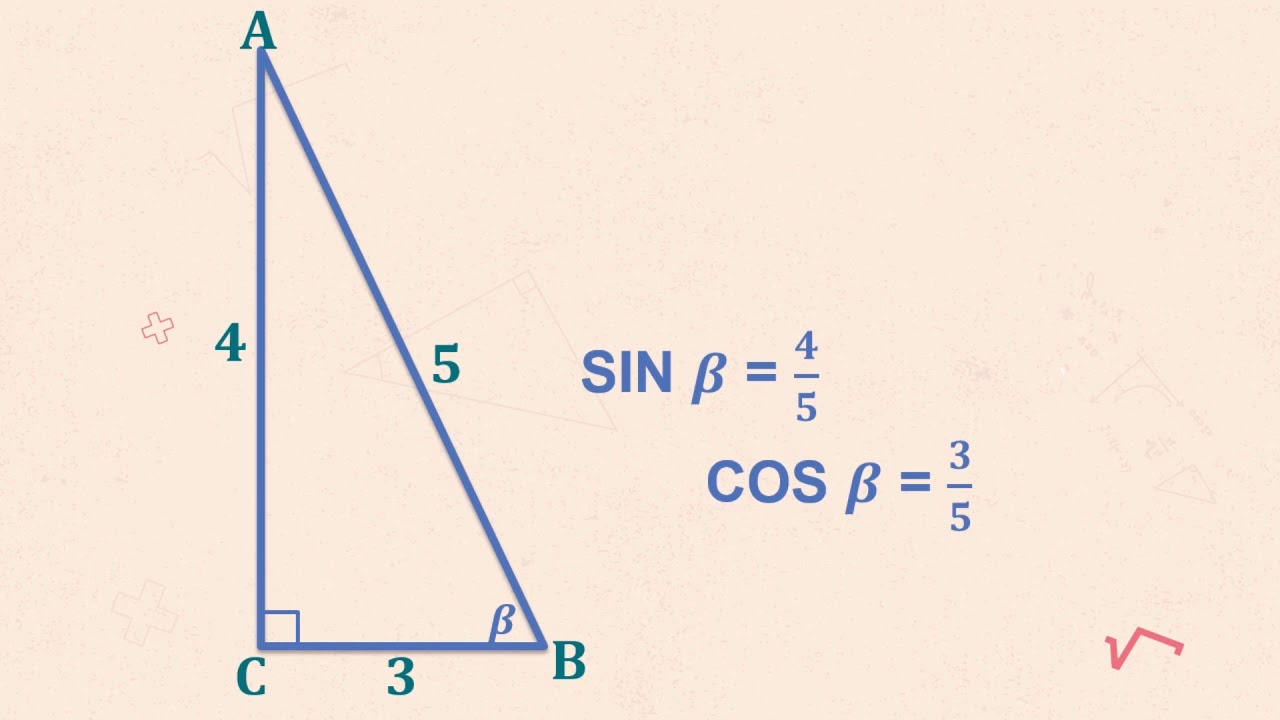
• 😀 The sine of an angle (sin θ) is the ratio of the side opposite the angle to the hypotenuse.
• 😀 The cosine of an angle (cos θ) is the ratio of the adjacent side to the hypotenuse.
• 😀 The tangent of an angle (tan θ) is the ratio of the side opposite the angle to the adjacent side.
• 😀 In real-world applications, trigonometry can be used to measure heights and distances, such as in the example with the height of a tower and the distance to a person standing at a point of observation.

Q & A

What is the Pythagorean Theorem and how is it applied in right-angled triangles?

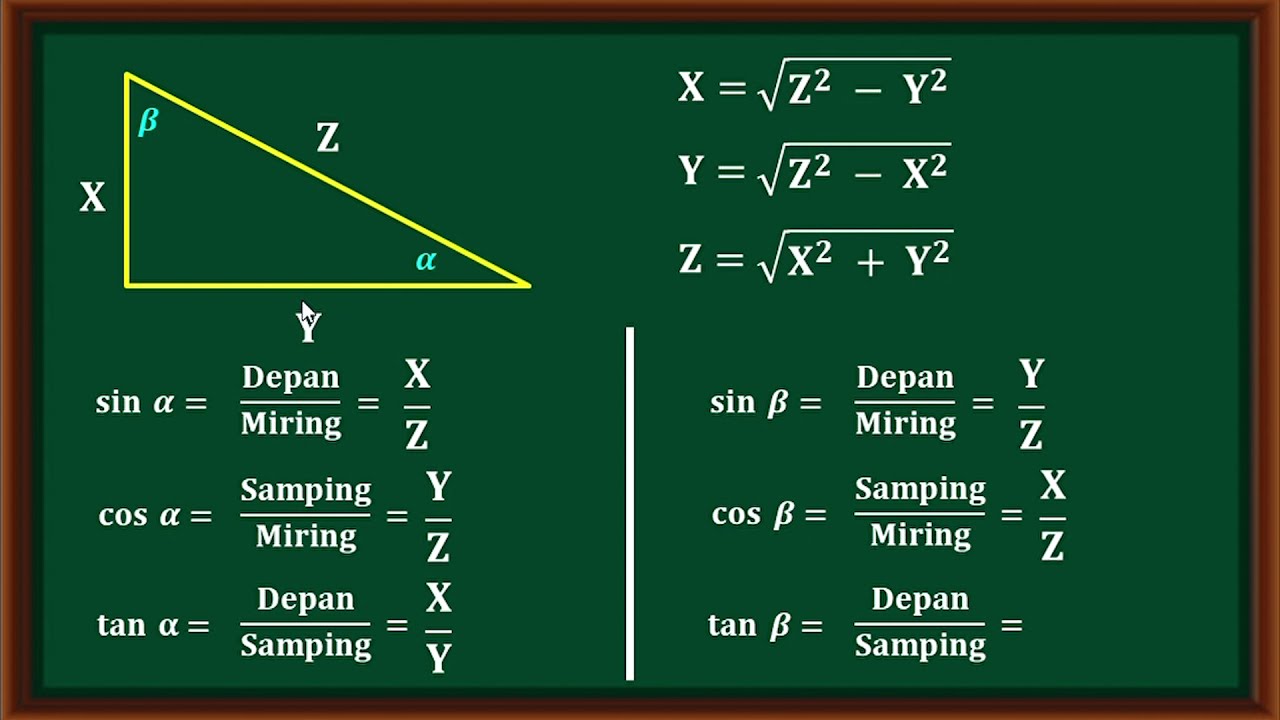
The Pythagorean Theorem states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. It is expressed as C² = A² + B². This theorem helps us calculate the length of any side in a right-angled triangle when the other two sides are known.

How can we find the value of a missing side in a right-angled triangle using the Pythagorean Theorem?

To find a missing side, rearrange the Pythagorean Theorem formula. For example, if you know the lengths of the two shorter sides (A and B), the hypotenuse (C) can be calculated using C = √(A² + B²). If the hypotenuse is missing, you can use A = √(C² - B²), and for the other side, B = √(C² - A²).

What are the three main trigonometric ratios, and how are they defined?

The three main trigonometric ratios are: 1. Sine (sin), defined as the ratio of the opposite side to the hypotenuse (sin(θ) = opposite/hypotenuse). 2. Cosine (cos), defined as the ratio of the adjacent side to the hypotenuse (cos(θ) = adjacent/hypotenuse). 3. Tangent (tan), defined as the ratio of the opposite side to the adjacent side (tan(θ) = opposite/adjacent).

How can you use trigonometric ratios to solve for unknown sides in a triangle?

To solve for an unknown side, you can use the appropriate trigonometric ratio based on the known values. For example, if you know the angle and one side, you can use sine, cosine, or tangent depending on the given side (opposite, adjacent, or hypotenuse). Rearrange the formula to solve for the missing side.

What is the value of sine, cosine, and tangent for special angles (30°, 45°, 60°)?

The values for the trigonometric ratios of special angles are: - For 30°: sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = 1/√3 - For 45°: sin(45°) = 1/√2, cos(45°) = 1/√2, tan(45°) = 1 - For 60°: sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3.

How do you calculate the height of a tree using trigonometry?

To calculate the height of a tree, use the angle of elevation from a specific point. If you know the distance from the tree and the angle, use the tangent ratio (tan(θ) = height/distance) to find the height. Rearrange the formula to height = tan(θ) * distance.

What is the difference between an angle of elevation and an angle of depression?

An angle of elevation is the angle formed between the horizontal ground and a line of sight looking upward at an object. An angle of depression is the angle formed between the horizontal ground and a line of sight looking downward at an object. Both are used in trigonometric calculations to find unknown distances or heights.

How can trigonometric ratios help in real-world applications like determining the height of a building?

Trigonometric ratios can be applied in real-world situations like determining the height of a building by measuring the angle of elevation from a certain distance. Using the tangent ratio (tan(θ) = height/distance), you can solve for the height if the distance and angle are known.

In the given example, how do we solve for side BC of a right-angled triangle if we know the length of AC and the angle 30°?

To find side BC, use the sine ratio (sin(30°) = opposite/hypotenuse). Since BC is opposite to the 30° angle and AC is the hypotenuse, rearrange the sine formula to BC = AC * sin(30°). If AC = 8√3, then BC = 8√3 * 1/2 = 4√3.

How do you solve for an unknown angle when the trigonometric ratios are known?

To solve for an unknown angle, use the inverse trigonometric functions (arcsin, arccos, or arctan). For example, if you know the sine of an angle, use arcsin to find the angle: θ = arcsin(opposite/hypotenuse). Similarly, use arccos or arctan depending on the given ratio.