04 Cómo usar la tabla de distribución normal

Summary

El guión de este video ofrece una explicación detallada sobre cómo utilizar la tabla de distribución normal estándar para calcular áreas y probabilidades asociadas con valores Z específicos. Se discuten los desafíos de la tabla, que solo proporciona áreas por debajo de un valor Z positivo y cómo se pueden resolver casos en los que se requiere el cálculo de áreas por encima de un valor positivo o negativo, o entre dos valores Z. Además, se destaca la simetría de la distribución normal y cómo se puede utilizar para encontrar áreas por encima de un valor negativo, que es igual a la probabilidad de estar por debajo del valor positivo equivalente. Finalmente, se explica cómo calcular la probabilidad de estar entre dos valores Z, subrayando la importancia de la tabla de distribución normal para encontrar probabilidades por debajo de ciertos valores. El video concluirá con ejemplos prácticos para ilustrar estos conceptos.

Takeaways

• 📊 La tabla de distribución normal es una herramienta que permite encontrar el resultado de integrales sin necesidad de calcularlas directamente.
• 🔍 La tabla de distribución normal está diseñada para una distribución normal con media en 0 y desviación típica de 1.
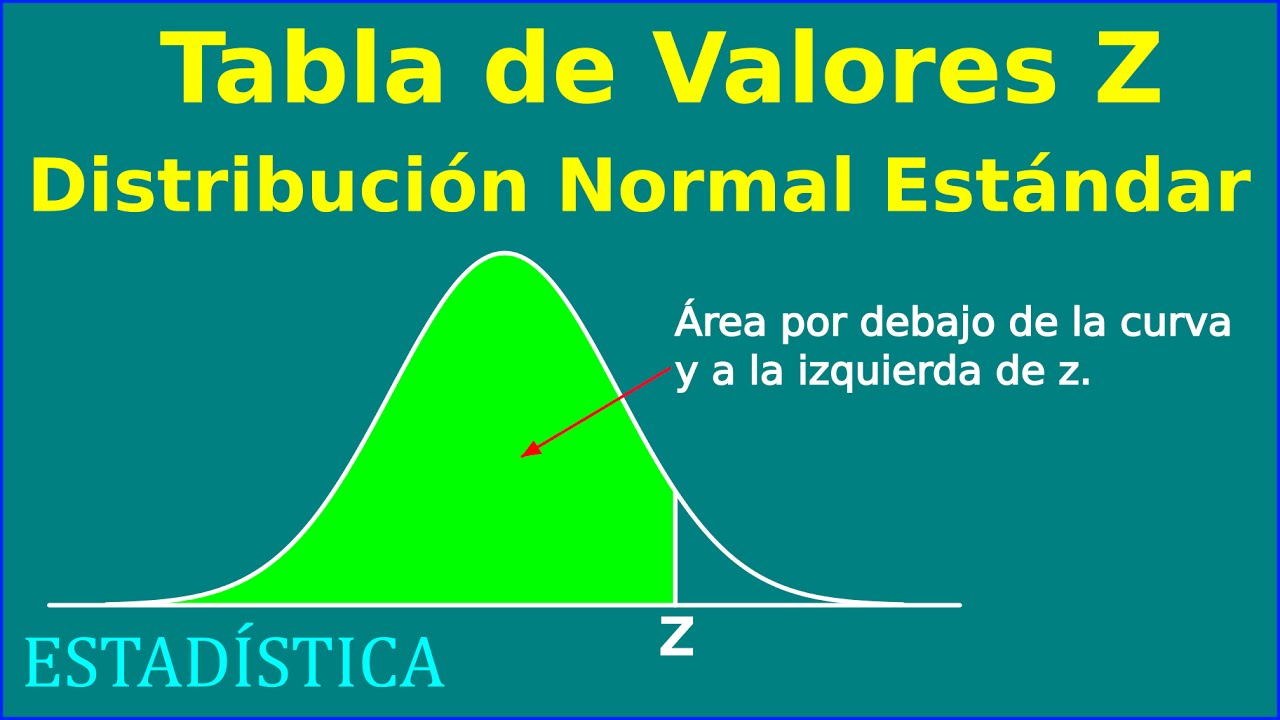
• 📉 La tabla proporciona la área bajo la curva de la distribución normal hasta un valor Z positivo específico.
• 🔁 La probabilidad de que un valor sea mayor que Z positivo se calcula como 1 menos la probabilidad de ser menor que Z.
• ↔️ La función de distribución normal es simétrica, por lo que la probabilidad de un valor ser mayor que Z negativo es la misma que ser menor que Z positivo.
• 🔢 Si se busca la probabilidad de un valor ser menor que Z negativo, se calcula como la probabilidad de ser mayor que Z positivo, cambiando el signo y el símbolo.
• 🚫 La tabla no proporciona directamente la probabilidad de que un valor sea mayor que un Z negativo.
• 🔴 La probabilidad de que un valor sea mayor que Z negativo se obtiene restando la probabilidad de ser menor que Z positivo de 1.
• 📌 Para calcular la probabilidad entre dos valores Z1 y Z2, se utiliza la probabilidad de ser menor que Z2 menos la probabilidad de ser menor que Z1.
• 💡 La tabla de distribución normal es una herramienta útil para calcular áreas y probabilidades en contextos de distribución normal.
• 📚 Es importante recordar y aplicar las reglas de la tabla de distribución normal para resolver diferentes casos de cálculo de probabilidades.

Q & A

¿Qué es la tabla de distribución normal y cómo se utiliza?

La tabla de distribución normal es una herramienta que permite encontrar la probabilidad de que una variable aleatoria normal esté por debajo de un valor Z específico. Se utiliza para evitar el cálculo de integrales complejas, proporcionando directamente el área bajo la curva de la distribución normal hasta un punto dado.

¿Por qué la tabla de distribución normal solo facilita valores para una distribución normal de media cero y desviación típica uno?

La tabla de distribución normal está estandarizada para una distribución normal con media en 0 y desviación típica en 1 porque esto simplifica los cálculos y permite la comparación entre diferentes conjuntos de datos que se ajustan a una distribución normal.

Si la tabla de distribución normal solo da el área por debajo de un valor Z positivo, ¿cómo se calcula el área por encima de ese valor?

Para calcular el área por encima de un valor Z positivo, se utiliza la relación de que el área total debajo de la curva es 1. Entonces, el área por encima de Z es 1 menos el área por debajo de Z, que se encuentra en la tabla.

¿Cómo se calcula la probabilidad de que un valor sea mayor a un número negativo utilizando la tabla de distribución normal?

Dado que la distribución normal es simétrica, la probabilidad de que un valor sea mayor a un número negativo (-Z) es la misma que la probabilidad de que sea menor a su valor positivo equivalente (Z). Por lo tanto, se busca en la tabla el área por debajo de Z y se utiliza la misma probabilidad para el negativo.

¿Cómo se calcula la probabilidad de que un valor esté entre dos valores Z1 y Z2 utilizando la tabla de distribución normal?

Para encontrar la probabilidad de que un valor esté entre Z1 y Z2, se resta la probabilidad de estar por debajo de Z1 al área por debajo de Z2, es decir, P(Z1 < Z < Z2) = P(Z < Z2) - P(Z < Z1).

¿Por qué la tabla de distribución normal no proporciona directamente el área por encima de un valor dado?

La tabla de distribución normal está diseñada para ser eficiente y estándar, proporcionando el área por debajo de Z, que es la parte más comúnmente utilizada en cálculos de probabilidad. El área por encima se deduce fácilmente como 1 menos el área por debajo.

¿Cómo se puede resolver el inconveniente de que la tabla solo proporciona el área por debajo de un valor Z positivo?

Se puede resolver calculando el complemento del área por debajo de Z, que es 1 menos el valor encontrado en la tabla, para obtener el área por encima de Z.

¿Qué se entiende por 'Z mayúscula' en el contexto de la tabla de distribución normal?

En el contexto de la tabla de distribución normal, 'Z mayúscula' se refiere al valor estándarizado de una variable aleatoria, es decir, la posición relativa de un punto dentro de la distribución normal estandarizada.

¿Cómo se utiliza la tabla de distribución normal para encontrar la probabilidad de que un valor esté por debajo de 0,34?

Para encontrar la probabilidad de que un valor esté por debajo de 0,34, se busca en la tabla de distribución normal el valor de Z correspondiente a 0,3 con un decimal de 0,04. El valor en la intersección de la fila y columna correspondiente da la probabilidad de estar por debajo de 0,34.

¿Cuál es la ventaja de utilizar la tabla de distribución normal en lugar de calcular integrales?

La ventaja principal es la eficiencia y la simplicidad. En lugar de calcular integrales complejas, la tabla proporciona directamente los resultados, lo que ahorra tiempo y reduce el riesgo de errores en el cálculo.

¿Cómo se calcula el área que queda por encima de un valor negativo utilizando la tabla de distribución normal?

Por la simetría de la distribución normal, el área por encima de un valor negativo (-Z) es igual al área por debajo del valor positivo equivalente (Z). Por lo tanto, se busca en la tabla el área por debajo de Z y se utiliza esa probabilidad para el negativo.