Asíntotas verticales, horizontales y oblicuas de una función racional
Summary
TLDREn este video, se explica cómo encontrar las asintotas de una función racional. Se toman tres ejemplos para ilustrar los casos de asintotas verticales, horizontales y oblicuas. Las asintotas verticales ocurren cuando el denominador se anula, lo cual se determina igualando el denominador a cero. Las asintotas horizontales son posibles solo si el grado del numerador es menor o igual al del denominador, y su valor es cero si el grados son iguales o menor que el del denominador. Finalmente, las asintotas oblicuas se presentan cuando el grado del numerador es uno más que el del denominador. El video también aborda cómo resolver la división de polinomios para encontrar la asintota oblicua, que se escribe en la forma mx + b, donde m es la pendiente de la línea. El contenido es presentado de una manera clara y detallada, facilitando la comprensión de los conceptos matemáticos.
Takeaways
- 📚 Aprender a sacar las asintotas de una función racional es el objetivo del vídeo.
- 🔍 Se explicarán tres tipos de asintotas: verticales, horizontales y oblicuas.
- 🚫 No siempre se presentarán los tres tipos de asintotas en una función racional.
- 📐 Asintotas verticales ocurren cuando el denominador se anula a cero.
- 🔢 Las asintotas verticales están representadas por la ecuación x = un número real.
- ↕️ Asintotas horizontales son posibles si el grado del numerador es menor o igual al del denominador.
- 🔺 Las asintotas horizontales están representadas por la ecuación y = un número real.
- ⛔ No pueden existir asintotas horizontales y oblicuas simultáneamente debido a condiciones contradictorias.
- 🔄 Asintotas oblicuas se presentan cuando el grado del numerador es uno más que el del denominador.
- 🔁 El proceso para encontrar la asintota oblicua implica dividir el numerador entre el denominador.
- 📈 La asintota oblicua resultante tiene la forma y = mx + b, donde m es la pendiente de la línea.
Q & A
¿Qué son las asíntotas verticales en una función racional?
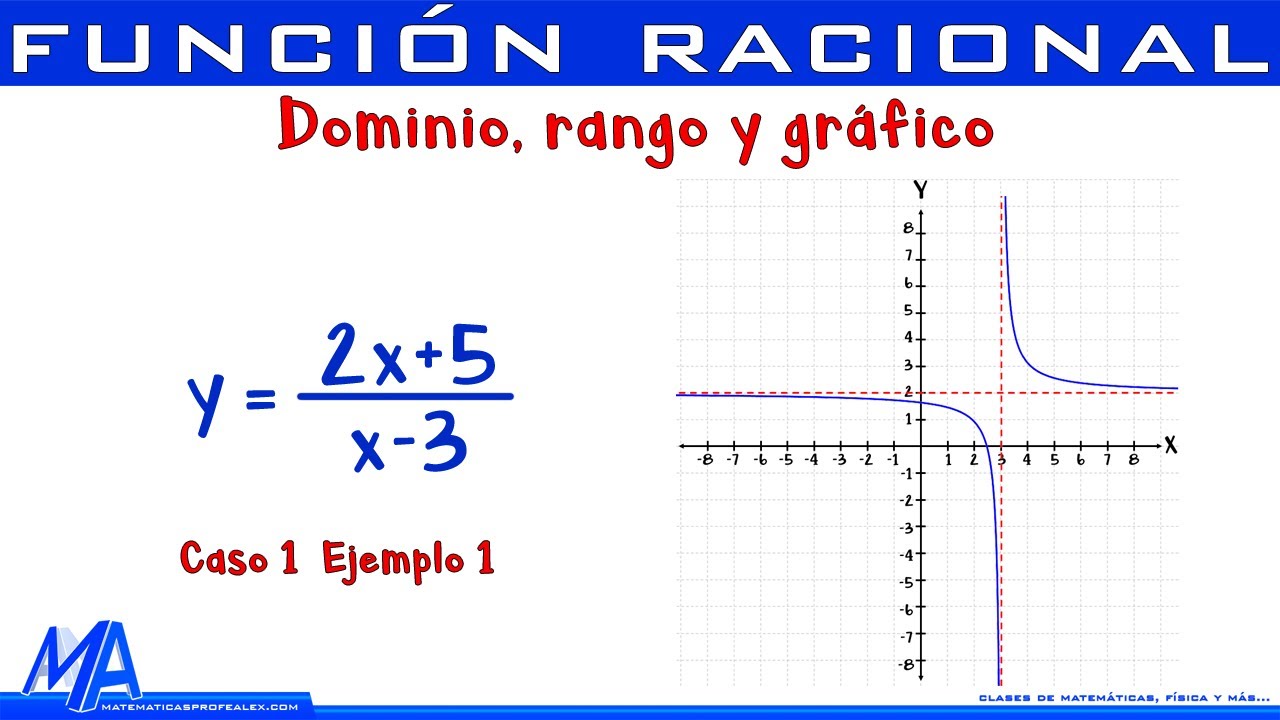
-Las asíntotas verticales son líneas que la función racional no puede cruzar. Se dan cuando el denominador de la función racional se anula, es decir, se convierte en cero.
¿Cómo se encuentran las asíntotas verticales de una función racional?
-Para encontrar las asíntotas verticales, se iguala el denominador de la función a cero y se resuelve para encontrar los valores de x que hacen que el denominador se anule.
¿Cuál es la forma general de las ecuaciones de las asíntotas verticales en una función racional?
-Las ecuaciones de las asíntotas verticales tienen la forma x = número, donde 'número' es el valor de x que hace que el denominador se anule.
¿Qué condiciones deben cumplirse para que una función racional tenga asíntotas horizontales?
-Para que una función racional tenga asíntotas horizontales, el grado del numerador debe ser menor o igual al grado del denominador.
¿Cómo se encuentran las asíntotas horizontales de una función racional si el grado del numerador y del denominador son iguales?
-Si el grado del numerador y del denominador son iguales, la asintota horizontal se encuentra dividiendo los coeficientes principales de los polinomios, que son los coeficientes de los términos de mayor grado.
¿Cuál es la forma general de las ecuaciones de las asíntotas horizontales en una función racional?
-Las ecuaciones de las asíntotas horizontales tienen la forma y = número, donde 'número' es el resultado de dividir el coeficiente principal del numerador entre el coeficiente principal del denominador.
¿Son posibles asíntotas horizontales y oblicuas al mismo tiempo en una función racional?
-No, es imposible tener asíntotas horizontales y oblicuas al mismo tiempo en una función racional, ya que las condiciones para su existencia son contradictorias.
¿Cuáles son las condiciones para que una función racional tenga asíntotas oblicuas?
-Las asíntotas oblicuas se presentan cuando el grado del numerador es exactly 1 unidad mayor que el grado del denominador.
¿Cómo se encuentra la asintota oblicua de una función racional?
-Para encontrar la asintota oblicua, se realiza la división polinomial del numerador entre el denominador, y el resultado es el cociente, que representa la ecuación de la asintota oblicua en la forma y = mx + b.
¿Por qué no todas las funciones racionales presentan los tres tipos de asíntotas?
-No todas las funciones racionales presentan los tres tipos de asíntotas porque cada tipo de asintota tiene condiciones específicas que deben cumplirse en cuanto al grado del numerador y del denominador, y no todas las funciones racionales satisfacen estas condiciones.
¿Cómo se identifica visualmente una asintota vertical en una gráfica de una función racional?
-Visualmente, las asíntotas verticales son líneas rectas que cortan el eje x en un punto específico y que la curva de la función no puede cruzar.
¿Qué sucede con la gráfica de una función racional cuando el grado del numerador es mayor que el del denominador?
-Cuando el grado del numerador es mayor que el del denominador, la gráfica de la función racional no tiene asíntotas horizontales, pero puede tener asíntotas oblicuas.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)