Multiplicity of zeros of polynomials | Polynomial graphs | Algebra 2 | Khan Academy
Summary
TLDRThis video explores the behavior of polynomial zeros through two polynomials, P1 and P2, focusing on the concept of multiplicity. While P1 has distinct zeros at x = 1, 2, and 3 with a sign change at each, P2 has a zero at x = 3 with multiplicity 2, leading to no sign change at that point. The video emphasizes that odd multiplicities result in a sign change, while even multiplicities do not. It also highlights the relationship between the number of zeros and the polynomial's degree, noting that the total multiplicity of zeros equals the degree.
Takeaways
- 😀 The script discusses two polynomials, P1 and P2, focusing on their zeros and graphical representation.
- 😀 Zeros of a polynomial are x-values where the polynomial equals zero, easily determined from its factored form.
- 😀 For polynomial P1, the zeros are at x = 1, x = 2, and x = 3, where the graph intersects the x-axis.
- 😀 The sign of the polynomial between consecutive zeros changes, indicating the behavior of the function.
- 😀 Polynomial P2, also a third-degree polynomial, has a unique zero at x = 1 and a multiplicity of two at x = 3.
- 😀 Multiplicity refers to the number of times a particular zero appears in the factored form of a polynomial.
- 😀 In P1, all zeros have a multiplicity of one, meaning they each change the sign of the polynomial.
- 😀 In P2, the zero at x = 3 has a multiplicity of two, resulting in no sign change at that zero.
- 😀 An odd multiplicity results in a sign change at the zero, while an even multiplicity results in no sign change.
- 😀 The total number of distinct zeros is less than or equal to the degree of the polynomial, influenced by multiplicities.
Q & A
What are the two polynomials discussed in the video?
-The two polynomials discussed are P1 and P2, which are presented in factored form.
How are the zeros of polynomial P1 determined?
-The zeros of polynomial P1 are found by setting the polynomial equal to zero, which occurs at x = 1, x = 2, and x = 3.
What does the graph of P1 indicate about its zeros?
-The graph of P1 shows that it intersects the x-axis at its zeros, indicating sign changes around each zero.
What unique feature does polynomial P2 have regarding its zeros?
-Polynomial P2 has a repeated zero at x = 3, which means it has a multiplicity of 2 for this zero.
What is the concept of 'multiplicity' in relation to polynomial zeros?
-Multiplicity refers to the number of times a zero is counted based on its factors; it affects the graph's behavior at that zero.
How does the multiplicity of a zero affect the graph of a polynomial?
-If a zero has an odd multiplicity, the graph crosses the x-axis, indicating a sign change. If it has an even multiplicity, the graph touches the x-axis without crossing it, resulting in no sign change.
What happens to the graph of P1 at its zeros?
-At each of its zeros, P1's graph crosses the x-axis, showing sign changes around each zero.
What is the relationship between the number of zeros and the degree of a polynomial?
-The number of zeros, when counted with their multiplicities, is at most equal to the degree of the polynomial.
What can be concluded about the behavior of P2 at x = 3?
-At x = 3, where P2 has a multiplicity of 2, the graph touches the x-axis but does not cross it, indicating no sign change.
How can one determine the total degree of a polynomial based on its zeros?
-The total degree of a polynomial is equal to the sum of the multiplicities of its zeros.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
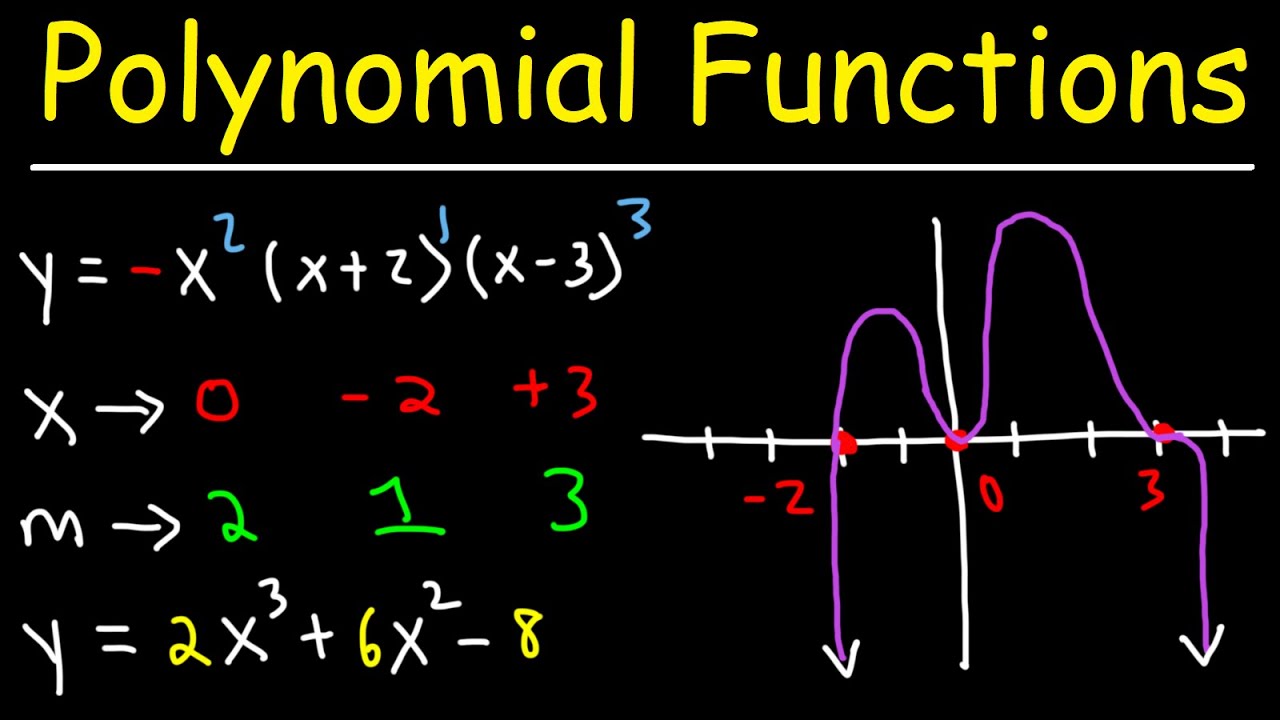
How To Graph Polynomial Functions Using End Behavior, Multiplicity & Zeros
Lesson 6.3 - Identifying a Polynomial Function from the Graph

Polynomials Class 10

Fundamental Theorem of Algebra

Graphs of Polynomials: Identification and Characterization

Ganzrationale Funktionen (Polynomfunktionen) - Einführung / Grundlagen
5.0 / 5 (0 votes)
