Ganzrationale Funktionen (Polynomfunktionen) - Einführung / Grundlagen
Summary
TLDRThis video explains the concept of polynomial functions, focusing on the term 'polynomial' and its relationship with 'rational functions'. It clarifies that polynomial functions consist of coefficients and powers of a variable, emphasizing that the exponents must be natural numbers and the coefficients real numbers. The video explores the structure of polynomials, using a general form to demonstrate how different degrees and terms are represented. Examples of quadratic, linear, and cubic functions are provided to illustrate key points. The video concludes with a focus on finding the roots of polynomial equations.
Takeaways
- 😀 Polynomial functions are often referred to as 'Ganzrationale Funktionen' in German, but the term 'polynomial functions' is more accurate, as used in English.
- 😀 A polynomial consists of coefficients and powers of the variable, where the powers are natural numbers, like x^4, x^3, x^2, etc.
- 😀 A polynomial equation is written in the form of terms added together, with the equation equal to 0, like 3x^4 + 2x^3 - x^2 + x - 5 = 0.
- 😀 Polynomials are represented as functions by adding f(x) before the expression, and the term 'Polynomfunktion' refers to this function form.
- 😀 Each term in a polynomial has a coefficient, which must be a real number, and the exponents must be natural numbers (0, 1, 2, 3, etc.).
- 😀 The term 'coefficient' comes from Latin, meaning 'to act together,' referring to the factor multiplying the power of x in a term.
- 😀 Exponents in polynomials must be natural numbers, meaning they cannot be negative or fractional, otherwise, the function would be a rational function.
- 😀 Rational functions are recognized by having negative exponents, like x^(-1), which is equivalent to 1/x.
- 😀 A general polynomial function is written as f(x) = a_n * x^n + a_(n-1) * x^(n-1) + ... + a_1 * x + a_0.
- 😀 A polynomial of degree 4, like the example given, has the highest exponent as 4, and is called a 'polynomial of degree 4'. If the highest exponent is 3, it is a 'polynomial of degree 3'.
- 😀 The most common types of polynomial functions are linear (degree 1), quadratic (degree 2), and cubic (degree 3) functions, each with their own unique characteristics and graphs.
Q & A
What are Ganzrationale Funktionen (Polynomial Functions)?
-Ganzrationale Funktionen, or Polynomial Functions, are mathematical functions consisting of terms with coefficients and powers of a variable, typically denoted as x. The exponents of x must be natural numbers (0, 1, 2, 3, ...), and the coefficients are real numbers.
What is the difference between Polynomial Functions and Rational Functions?
-Polynomial Functions have natural number exponents for the variable, and the coefficients are real numbers. Rational Functions, on the other hand, may have negative exponents, which would place the variable x in the denominator, resulting in a fraction.
What is a coefficient in a polynomial function?
-A coefficient is a constant multiplier in front of a term with a power of x. For example, in the term 3x^4, 3 is the coefficient. Coefficients can be any real number, including integers, fractions, and even irrational numbers.
What does the term 'Polynom 4. Grades' mean?
-The term 'Polynom 4. Grades' refers to a polynomial of degree 4, meaning that the highest exponent of the variable x is 4. This polynomial has terms like x^4, x^3, x^2, x, and a constant term.
How do we represent a general polynomial function?
-A general polynomial function can be represented as f(x) = a_n * x^n + a_(n-1) * x^(n-1) + ... + a_1 * x + a_0, where a_n, a_(n-1), ..., a_0 are real coefficients, and n is the highest exponent (degree) of the polynomial.
Why are negative exponents not allowed in polynomial functions?
-Negative exponents in a polynomial would create fractions, placing the variable x in the denominator. This would make the function a rational function, not a polynomial function.
What is a linear function?
-A linear function is a polynomial of degree 1, represented by a term like ax + b, where a and b are constants, and the graph of this function is a straight line.
What is a quadratic function?
-A quadratic function is a polynomial of degree 2, typically written as f(x) = ax^2 + bx + c. Its graph is a parabola, and the highest exponent of x is 2.
What is the significance of the term x^0 in polynomial functions?
-In polynomial functions, x^0 equals 1, which is why the constant term (like -5 in the example) is considered as part of the polynomial. It is the term where the exponent of x is zero.
How do we find the roots or zeroes of a polynomial function?
-To find the roots of a polynomial function, we set the equation equal to zero and solve for the variable x. For example, in the equation 3x^4 + 2x^3 - x^2 + x - 5 = 0, we solve for the values of x that satisfy this equation.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Grade 10 - Illustrating and graphing polynomial functions | SirABC

Illustrate Polynomial Functions | Second Quarter | Grade 10 MELC
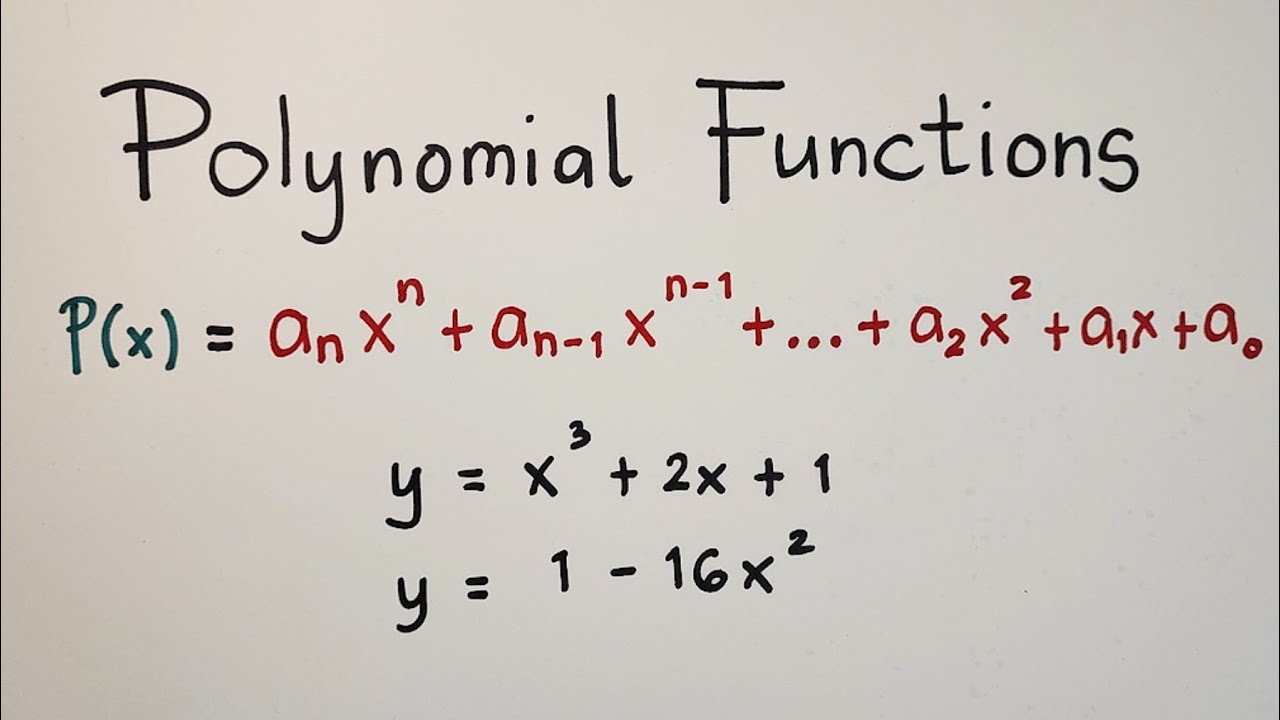
Polynomial Functions - Polynomial Function or NOT? Grade 10 Math Second Quarter

REPRESENT REAL-LIFE SITUATIONS USING RATIONAL FUNCTIONS || GRADE 11 GENERAL MATHEMATICS Q1

Graphs of Polynomials: Identification and Characterization

ILLUSTRATING POLYNOMIAL FUNCTIONS || GRADE 10 MATHEMATICS Q2
5.0 / 5 (0 votes)