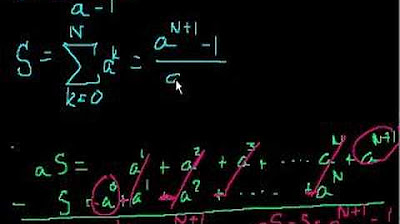Deret Geometri Tak Hingga | Matematika Kelas X Fase E Kurikulum Merdeka
Summary
TLDRThe video discusses infinite geometric series, using the example of a bouncing tennis ball to illustrate the concept. It explains how the ball, dropped from a height of 1 meter and bouncing back to one-fourth of its previous height, can be analyzed using the geometric series formula. The presenter also explores practical scenarios, such as calculating the total distance traveled by the ball and the perimeter of various geometric shapes. Overall, the content aims to make the principles of geometric series relatable and applicable in real-world contexts.
Takeaways
- 😀 Infinite geometric series require the common ratio (r) to be a fraction between -1 and 1.
- 🎾 The example of a bouncing tennis ball illustrates how to calculate the total distance traveled before it comes to a stop.
- 📏 The formula for the sum of an infinite geometric series is S = A / (1 - r) when |r| < 1.
- 📉 The height of each bounce of the tennis ball is reduced to 1/4 of the previous height.
- 🔢 An example calculation demonstrates how to find the total distance traveled by the ball using the infinite series formula.
- 🏀 A problem involving a ball dropped from a height of 8 meters with a bounce ratio of 3/5 is used to illustrate practical applications.
- 🧮 The total distance traveled by the bouncing ball can be calculated as 32 meters based on the given height and ratio.
- 📐 The discussion includes calculating the perimeter of squares and rectangles, utilizing the Pythagorean theorem.
- 🔍 Examples reinforce the understanding of geometric series through real-world scenarios.
- 💡 The session concludes with an encouragement to continue learning and exploring more mathematics topics.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is infinite geometric series in mathematics.
How does the example of a bouncing ball illustrate the concept of a geometric series?
-The bouncing ball is dropped from a height of 1 meter and continues to bounce back to 1/4 of its previous height, demonstrating how the heights form a geometric series.
What is the formula for the sum of an infinite geometric series?
-The formula for the sum of an infinite geometric series is S = A / (1 - r), where A is the first term and r is the common ratio.
In the bouncing ball example, what happens to the height of the ball as it continues to bounce?
-As the ball continues to bounce, its height decreases exponentially, approaching zero but never actually reaching it.
What ratio is used in the example with the bouncing ball?
-The ratio used in the example is 1/4, indicating that each bounce reaches a height that is 1/4 of the height of the previous bounce.
What is the significance of the ratio being between -1 and 1?
-A ratio between -1 and 1 ensures that the geometric series converges, allowing for a finite sum.
How is the total distance traveled by the ball calculated?
-The total distance is calculated using the geometric series formula, taking into account the distances of both the upward and downward movements of the ball.
Can you explain the example of a ball dropped from 8 meters?
-In this example, the ball falls from a height of 8 meters and bounces back to 3/5 of its height, requiring a calculation of the total distance traveled until it comes to a stop.
What method is used to calculate the perimeter of various geometric shapes in the lesson?
-The perimeter is calculated using the formula for the circumference of the shapes and considering the dimensions provided in the examples.
What is the conclusion drawn from the lesson on geometric series?
-The conclusion emphasizes the importance of understanding geometric series and encourages students to continue exploring mathematical concepts.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)