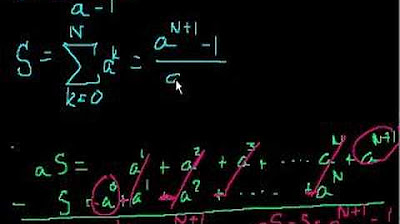deret geometri tak hingga bagian 1

Summary

This video tutorial explains infinite geometric series, focusing on how to calculate their sums. It introduces the basic concepts of convergent and divergent series, explaining the significance of the common ratio. The instructor covers different types of problems, such as finding the sum when the first term and common ratio are known, and solving for unknown terms or ratios based on the sum. With clear step-by-step examples, the video provides useful strategies and formulas, ensuring learners can tackle a variety of geometric series problems. The tutorial is ideal for students seeking to master infinite geometric series.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

Q & A

What is the main focus of the video script?

The video script primarily focuses on explaining infinite geometric series, with an emphasis on different types, formulas, and examples for converging and diverging series.

What is the difference between convergent and divergent geometric series?

A convergent series has a sum that approaches a specific value as the number of terms increases, while a divergent series increases or decreases without approaching any fixed number, continuing to grow or shrink indefinitely.

How can you identify if a geometric series is convergent or divergent?

A geometric series is convergent if the absolute value of the common ratio (r) is less than 1. If the absolute value of r is greater than or equal to 1, the series is divergent.

What formula is used to calculate the sum of an infinite convergent geometric series?

The sum of an infinite convergent geometric series is calculated using the formula: S = a / (1 - r), where 'a' is the first term and 'r' is the common ratio.

In the script, what is the geometric series example that demonstrates convergence?

The example where the terms are 1/2, 1/4, 1/8, 1/16, and so on is a convergent geometric series, with a common ratio of 1/2.

What is the geometric series example that demonstrates divergence?

The example where the terms are 1, 2, 4, 8, 16, and so on is a divergent series, with a common ratio of 2.

How do you calculate the sum of a convergent geometric series with a common ratio of 1/2 and first term 18?

Using the formula S = a / (1 - r), where a = 18 and r = 1/2, the sum is 18 / (1 - 1/2) = 18 / 1/2 = 36.

What is the key difference between the second and third types of problems described in the script?

The second type involves calculating the sum of an infinite geometric series when the first term and the total sum are known, while the third type requires finding the common ratio and a specific term when the second term and sum are given.

How is the common ratio (r) determined in a geometric series when the first term (a) and the total sum (S) are known?

The common ratio (r) can be calculated by rearranging the sum formula S = a / (1 - r) to solve for r, using the given values of the first term and total sum.

What happens when the common ratio in a geometric series is negative?

If the common ratio is negative, the terms of the series alternate in sign, and the series can still converge if the absolute value of r is less than 1. The convergence criterion remains the same.