06 Mirror Reflections
Summary
TLDRIn this lesson on geometric transformations, the focus is on mirror reflection. The instructor explains how mirror reflection maps a pre-image across a designated axis, emphasizing that this transformation acts as a perpendicular bisector for connecting corresponding points. Symmetry is introduced as a key concept, illustrating how objects can map onto themselves. The lesson includes examples using coordinate planes and manual transformations, as well as applications in Philippine fabrics, showcasing motifs through mirror reflection. The session concludes with a preview of the next topic: rotation transformations.
Takeaways
- 😀 Mirror reflection is a geometric transformation that maps a pre-image across a line known as the axis of mirror reflection.
- 😀 The concept of mirror reflection involves folding a plane along the axis so that the pre-image and its image overlap completely.
- 😀 Corresponding points, such as ears in a face, connect through line segments that are parallel to the axis of mirror reflection.
- 😀 The axis of mirror reflection acts as the perpendicular bisector for all line segments connecting corresponding points.
- 😀 A mirror reflection is an orientation-reversing transformation, meaning it alters the direction of the object.
- 😀 Symmetry is defined as a geometric transformation that maps an object onto itself, demonstrating mirror symmetry in various objects.
- 😀 On a coordinate plane, specific equations represent lines that act as axes of mirror reflection, influencing how points are transformed.
- 😀 The process of reflecting points involves identifying their positions before and after the transformation based on the axis.
- 😀 In applications like GeoGebra, a tool is available to facilitate mirror reflection transformations on figures.
- 😀 The video concludes with a brief mention of upcoming topics, specifically rotation transformations, indicating a progression in learning geometric transformations.
Q & A
What is mirror reflection in geometric transformations?
-Mirror reflection is a transformation that maps a pre-image across a designated line called the axis of mirror reflection, effectively flipping the image over that line.
What role does the axis of mirror reflection play in the transformation?
-The axis of mirror reflection acts as a perpendicular bisector for line segments connecting corresponding points of the pre-image and the reflected image, ensuring that these segments are equidistant from the axis.
How does mirror reflection reverse orientation?
-Mirror reflection is considered an orientation-reversing transformation because the reflected image has a different orientation compared to the original pre-image.
What is the definition of symmetry in geometry?
-Symmetry in geometry refers to a transformation that maps an object onto itself, meaning the object appears unchanged when a specific transformation is applied.
Can you give an example of a geometric figure exhibiting mirror symmetry?
-An example of mirror symmetry is the Philippine flag, where folding it along the axis of reflection would show the sun and stars overlapping with their original positions.
How do you identify corresponding points in mirror reflection?
-Corresponding points in mirror reflection are those that are directly across from each other with respect to the axis of mirror reflection, meaning they are equidistant from this axis.
What happens to the coordinates of points when reflected across the line y=x?
-When points are reflected across the line y=x, their coordinates are switched; for example, a point (x, y) becomes (y, x) after the reflection.
What tools can be used to perform mirror reflections in a coordinate plane?
-Software like GeoGebra can be used to visually demonstrate mirror reflections by allowing users to select objects and reflect them over specified lines.
How can mirror reflections be observed in Philippine fabric patterns?
-Mirror reflections can be observed in the motifs of Philippine fabrics, where applying the concept of reflection can create symmetrical designs, enhancing their aesthetic appeal.
What is the significance of understanding mirror reflections in geometry?
-Understanding mirror reflections is significant as it provides foundational knowledge for exploring more complex geometric transformations such as rotations and translations, which are crucial in various mathematical applications.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Transformasi Geometri [Part 1] - Refleksi (Pencerminan)

TRANSFORMAÇÕES ISOMÉTRICAS E HOMOTÉTICAS

Kelas 9 matematika || Transformasi Geometri || Refleksi atau Pencerminan

TRANSFORMASI FUNGSI PART 1

Kekongruenan Hal 177-180 Bab 3 TRANSFORMASI Kelas 9 SMP Kurikulum Merdeka
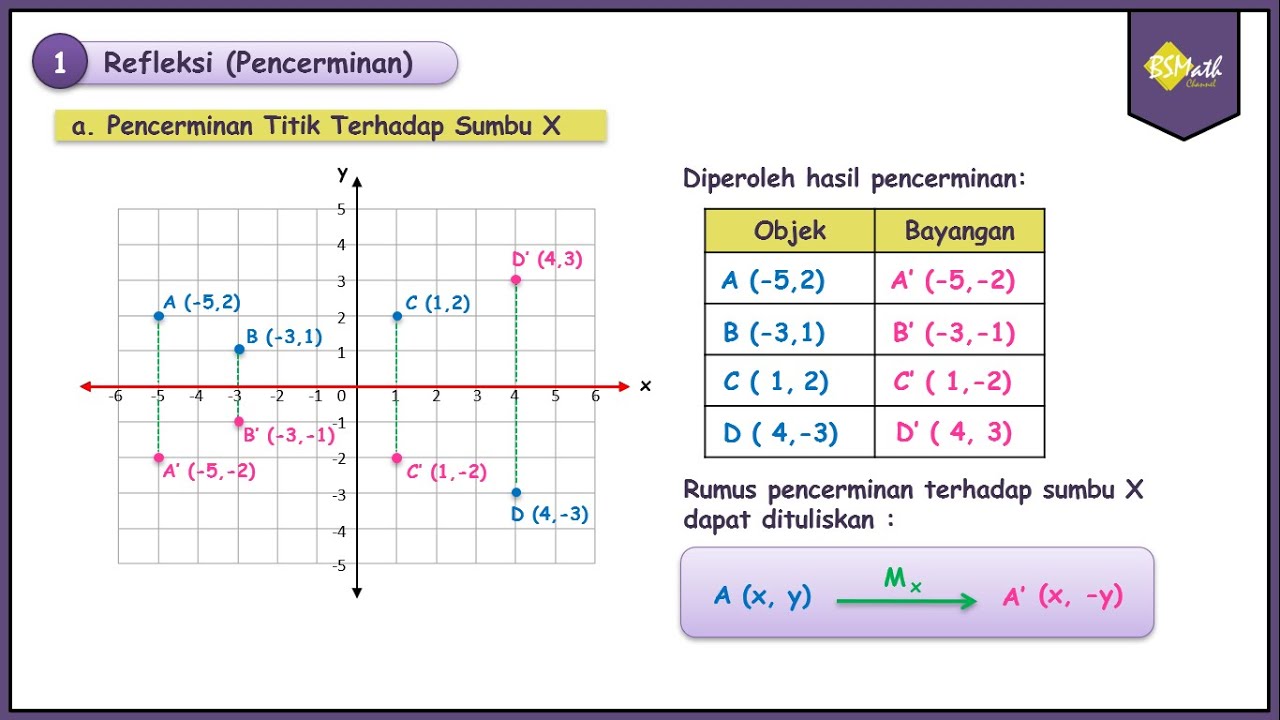
Transformasi Refleksi, Pencerminan Titik Terhadap Sumbu X - Matematika Tingkat Lanjut Kelas XI
5.0 / 5 (0 votes)
