Kekongruenan Hal 177-180 Bab 3 TRANSFORMASI Kelas 9 SMP Kurikulum Merdeka
Summary
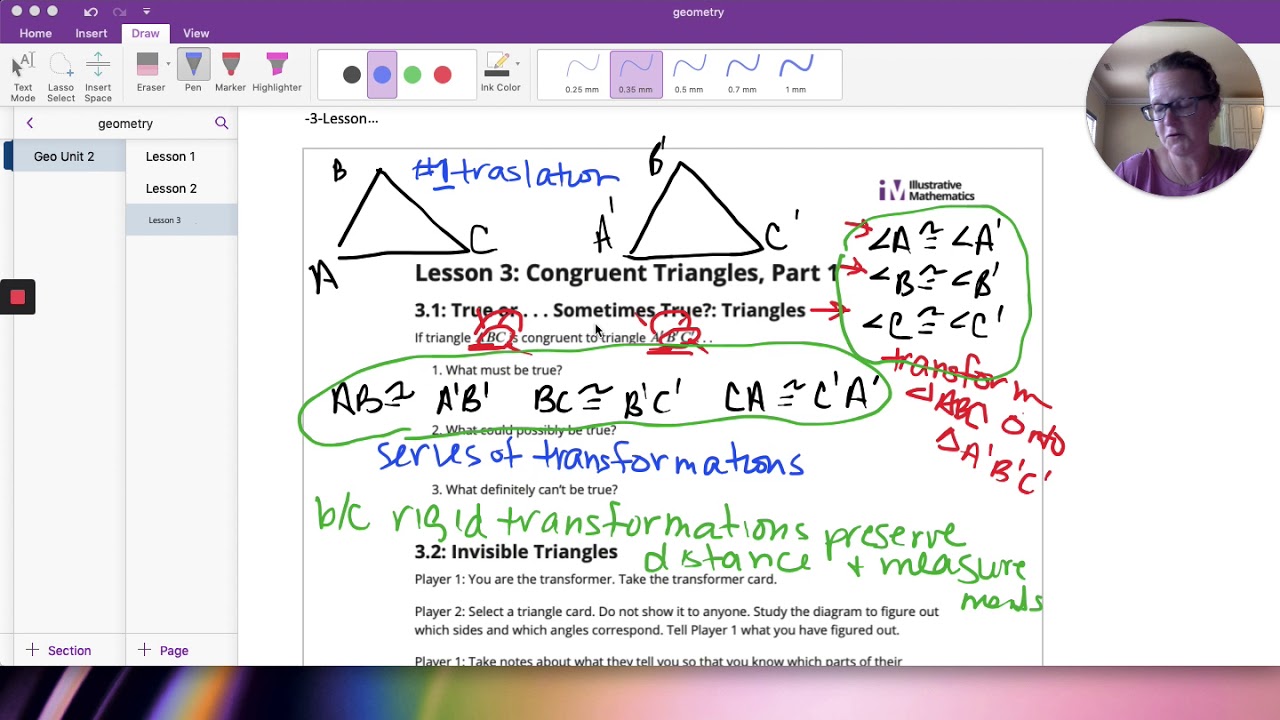
TLDRThis video lesson explores the concept of congruence in geometry, focusing on rigid transformations like translation, rotation, and reflection. It explains that two shapes are congruent if they have the same size and shape and can be aligned using these transformations. Through various examples, such as comparing right triangles and trapezoids, the lesson demonstrates how to prove congruence and non-congruence using transformations. The lesson encourages students to think creatively about applying transformation sequences to match shapes, enhancing their understanding of geometric congruence.
Takeaways
- 😀 Geometry transformation is the focus of the lesson, specifically on congruence in flat shapes.
- 😀 Congruence is defined as two flat shapes having the same size and shape.
- 😀 Example given: Two right-angled triangles of the same size and angles are congruent.
- 😀 Congruent shapes can be transformed through rigid transformations like translation, reflection, or rotation.
- 😀 To determine if two shapes are congruent, a rigid transformation or a series of such transformations must align the two shapes perfectly.
- 😀 Shapes with the same size but different curvature (like in the example with the blue and red shapes) may not be congruent.
- 😀 To prove two shapes are congruent, you must show they have identical form and size through a rigid transformation.
- 😀 If shapes have different forms or sizes, they are not congruent, which can be proven through observation of differences.
- 😀 The lesson emphasizes understanding transformations such as rotation and translation to test congruence.
- 😀 The lesson also asks students to creatively think about how transformations can align two shapes in different ways.
Q & A
What is the definition of congruency in geometry?
-Congruency in geometry refers to two shapes that have the same size and shape. This means that one shape can be transformed into the other through rigid transformations like translation, rotation, or reflection without altering its size or shape.
What are the three types of rigid transformations discussed in the lesson?
-The three types of rigid transformations discussed are translation, reflection, and rotation. These transformations preserve the size and shape of the figure.
Can two shapes be congruent if they have different sizes?
-No, two shapes cannot be congruent if they have different sizes. For congruency, the shapes must be identical in both size and shape.
How can we determine if two shapes are congruent?
-To determine if two shapes are congruent, we need to show that they have the same shape and size. We can also demonstrate that one shape can be transformed into the other through a rigid transformation such as translation, reflection, or rotation.
What is the significance of rigid transformations in proving congruency?
-Rigid transformations are significant because they allow us to prove congruency by demonstrating that one shape can be mapped onto another without changing its size or shape. This ensures that the two shapes are identical in both size and form.
What was the key observation in Example 3.5 regarding congruent shapes?
-In Example 3.5, we observed that two shapes (a trapezium in this case) were congruent because one could be transformed into the other by a rotation. This demonstrated that congruency can be proven by rigid transformations.
What is the difference between congruent and non-congruent shapes, as shown in the lesson?
-Congruent shapes are identical in both size and shape, whereas non-congruent shapes either have different sizes or shapes. For example, in one diagram, two shapes with the same size but different curvatures were not congruent because their shapes were not identical.
Why is it important to show that two shapes have the same size and shape when proving congruency?
-It is important because congruency is defined by identical size and shape. If two shapes differ in either dimension, they cannot be considered congruent. The demonstration of identical size and shape ensures that the transformation is valid.
What transformations did Ahmad perform in his example to show congruency?
-Ahmad performed a rotation of 90 degrees around a point and then a translation to show that one shape could be transformed into another. This sequence of transformations allowed him to demonstrate that the two shapes were congruent.
What is the role of creative thinking in understanding congruency and transformations?
-Creative thinking plays a role in finding different ways to apply transformations and test congruency. By considering various sequences of transformations, students can deepen their understanding of how shapes relate to one another and how transformations affect their properties.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)