Kelas 9 matematika || Transformasi Geometri || Refleksi atau Pencerminan

Summary

This video lesson focuses on the concept of geometric transformations, specifically reflection (or mirror symmetry). It explains how shapes, such as triangles, can be reflected across various lines, including the x-axis, y-axis, and other specific lines like y = x. The video covers key properties of reflection, such as distances being preserved and shapes maintaining their size and orientation. It also provides several examples and mathematical formulas for different types of reflections, making the topic clear for students to understand and apply in geometry.

Takeaways

• 😀 Reflections (or mirror images) are a type of geometric transformation that moves an object using the concept of a mirror image.
• 😀 When reflecting a geometric object like a triangle, the image is created by measuring the distance from each point to a mirror line (such as line K in the example).
• 😀 The reflection follows specific properties, such as the distance between the object and the mirror line being equal to the distance between the image and the mirror line.
• 😀 In a reflection, the shape and size of the object remain unchanged, but the orientation may change (for example, a triangle becomes a mirrored version).
• 😀 Reflections can occur over various lines, such as the X-axis, Y-axis, and lines like y = x or y = -x.
• 😀 The first property of reflection is that the line connecting a point to its image will always be perpendicular (at a right angle) to the mirror line.
• 😀 The second property of reflection is that the distance from any point to the mirror line is the same as the distance from the image point to the mirror line.
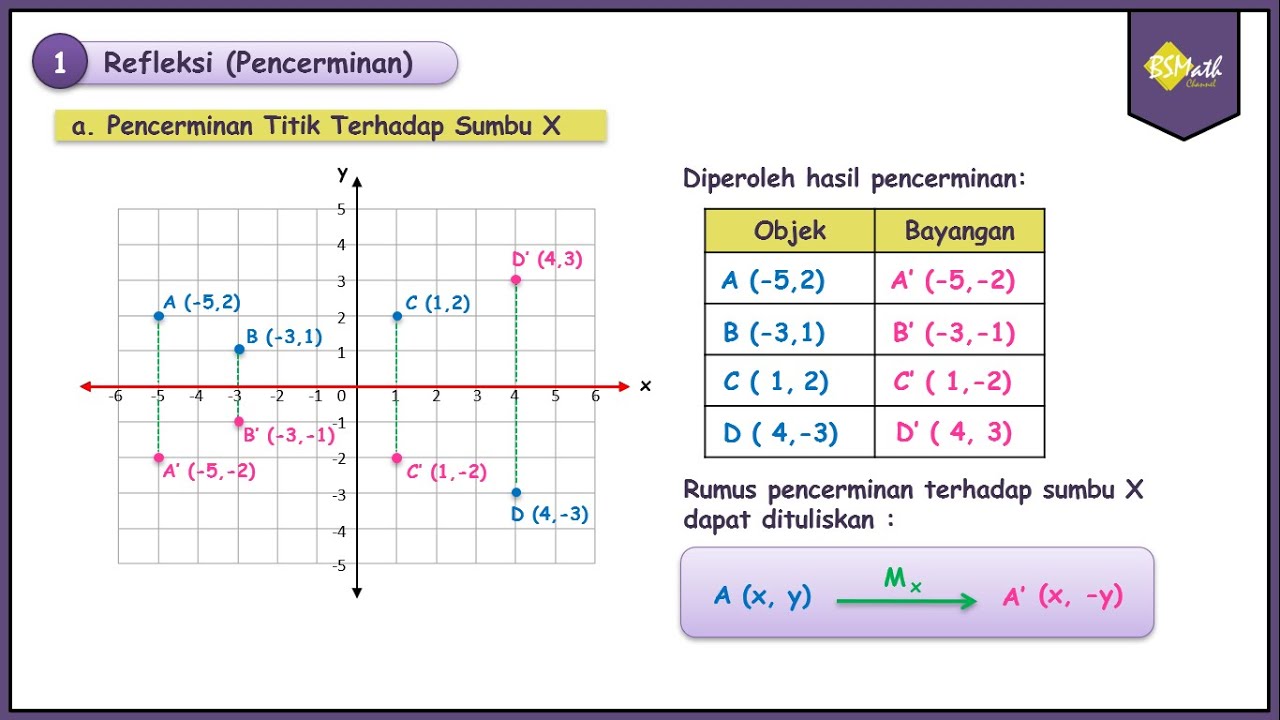
• 😀 Reflections can be performed over different axes: for example, reflecting over the X-axis results in a change in the Y-coordinate of the point.
• 😀 Similarly, reflecting over the Y-axis results in a change in the X-coordinate of the point.
• 😀 Reflections can also be performed over lines like y = x and y = -x, with the rule being that the coordinates of a point swap or change signs accordingly.

Q & A

What is reflection (refleksi) in geometry?

Reflection is a type of geometric transformation that moves every geometric object by using the properties of a mirror image.

How does reflection work with the example of triangle ABC?

In the example, triangle ABC is reflected over a line K, and the reflection of each point (A, B, C) is calculated based on their distance to the line K.

What is the first property of reflection?

The first property is that the line connecting an object to its reflection is perpendicular to the mirror line.

What is the second property of reflection?

The second property is that the distance from the object to the mirror line is the same as the distance from its reflection to the mirror line.

What is the third property of reflection?

The third property is that the shape and size of the reflection are identical to the original object.

What happens when a point is reflected across the x-axis?

When a point (x, y) is reflected across the x-axis, its y-coordinate changes sign, while the x-coordinate remains the same, resulting in the point (x, -y).

How does reflection across the y-axis work?

When a point (x, y) is reflected across the y-axis, its x-coordinate changes sign, while the y-coordinate remains unchanged, resulting in the point (-x, y).

What happens when a point is reflected across the origin (0,0)?

When a point (x, y) is reflected across the origin, both the x and y coordinates change signs, resulting in the point (-x, -y).

What is the reflection formula for reflecting over the line y = x?

The reflection of a point (x, y) over the line y = x results in the point (y, x), effectively swapping the x and y coordinates.

How does reflection across the line y = -x work?

When a point (x, y) is reflected across the line y = -x, the reflection is given by the point (-y, -x), where both the x and y coordinates change signs and are swapped.