4.1: The Story So Far
Summary
TLDRThis lecture explores linear models in depth, discussing how they fit hyperplanes through weighted sums of input features. In regression, the goal is to position data points close to the hyperplane, while in binary classification, the hyperplane separates data into distinct classes. The concept of margins is introduced, quantifying prediction strength and correctness. Transformations through basis expansion can create complex decision boundaries in the original feature space. However, the choice of basis functions poses challenges, particularly in high-dimensional spaces, making domain knowledge crucial for effective modeling.
Takeaways
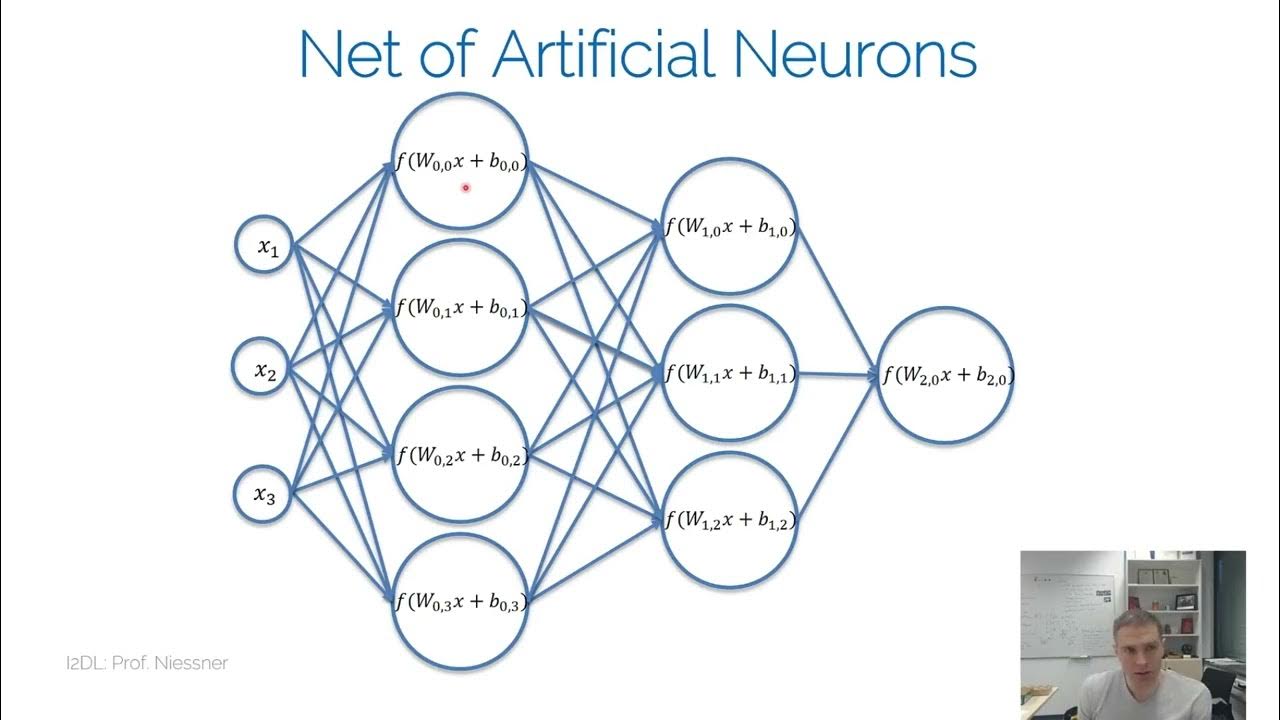
- 😀 Linear models utilize a hyperplane defined by a weighted sum of input features to represent data.
- 📈 In regression tasks, the aim is for data points to closely align with the hyperplane that predicts their values.
- 🔍 Classification problems use the hyperplane to separate feature space into distinct regions for positive and negative labels.
- ✅ Data that can be perfectly divided by a hyperplane is referred to as linearly separable.
- 🧩 Multiclass classification requires fitting multiple hyperplanes and can be approached through pairwise comparisons or softmax classification.
- 📊 Outputs of linear models are interpreted as scores indicating the confidence of sample class membership.
- ⚖️ Nonlinear functions like sigmoid or softmax are often applied to model outputs to ensure probability distributions are valid.
- 📏 The margin of a prediction, calculated as the product of the label and score, reflects the strength and correctness of the prediction.
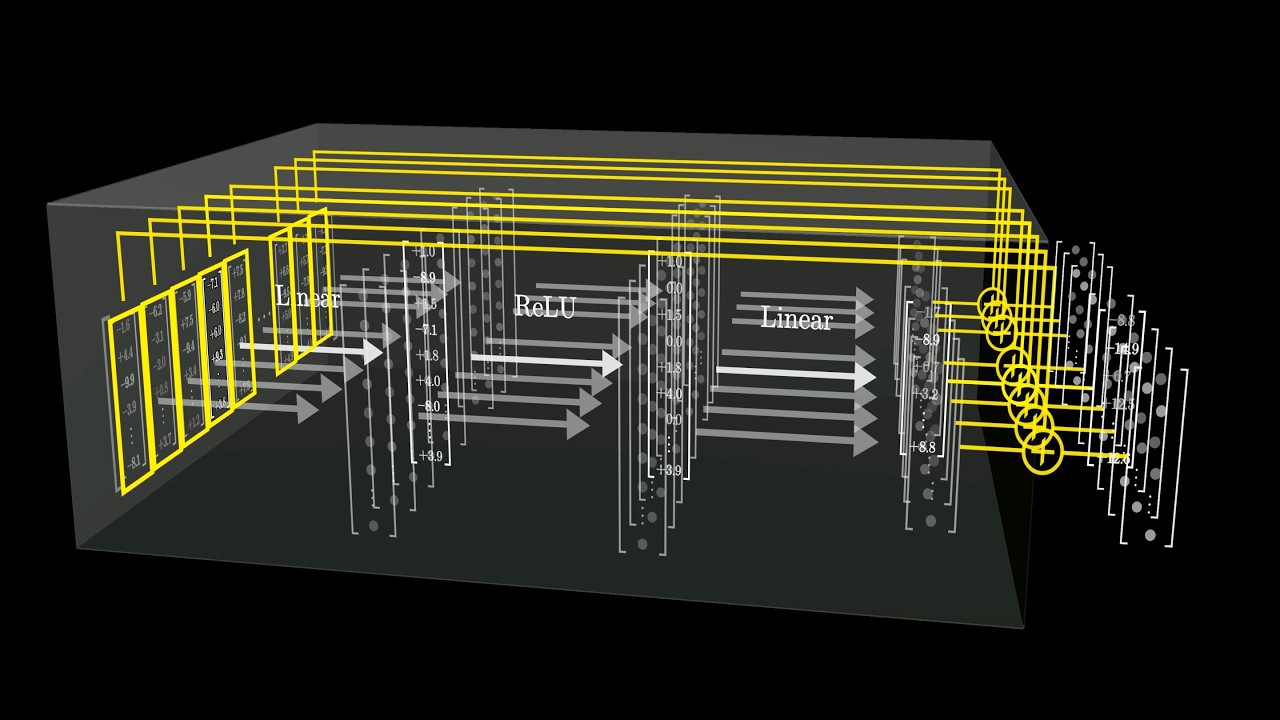
- 🔄 Basis expansion allows the application of transformations to data before it is input into linear models, leading to complex decision boundaries.
- 💡 Selecting effective basis functions for transformations can be challenging without domain knowledge, and high-dimensional computations may be costly.
Q & A
What is the primary function of linear models in machine learning?
-Linear models fit a hyperplane by taking a weighted sum of input features, aiming to predict outcomes in regression and classification tasks.
How do linear models handle regression problems?
-In regression, linear models aim for data points to be close to the hyperplane, and losses are calculated to capture this closeness.
What role does the hyperplane play in binary classification?
-In binary classification, the hyperplane divides the feature space into two disjoint half-spaces, assigning positive or negative labels to the samples.
What is meant by 'linearly separable' data?
-Data that can be perfectly split by a hyperplane is referred to as linearly separable.
How are multiple classes handled in linear models?
-For multiclass problems, multiple hyperplanes are fitted, and methods like pairwise comparisons or softmax classification can be used.
What do the outputs of a linear model represent in classification tasks?
-The outputs can be interpreted as scores that estimate the likelihood of a sample belonging to a specific class.
What is the significance of the margin in classification?
-The margin, which is the label multiplied by the score output, indicates the strength and correctness of a prediction; a positive margin means correct classification, while a negative margin indicates an error.
What is basis expansion in the context of linear models?
-Basis expansion involves transforming input data using a set of fixed functions, allowing the linear model to fit a hyperplane in a new feature space, which can represent more complex decision boundaries.
What challenges are associated with choosing basis functions for transformations?
-Choosing the right basis functions can be difficult without specific domain knowledge, and transformations can be computationally expensive, especially in high-dimensional spaces.
What are common nonlinear functions applied to linear model outputs?
-Common nonlinear functions include the sigmoid and softmax functions, which help ensure that the probabilities derived from the scores add up to one.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)