Importance of Growth Rate

Summary

In this lecture, the importance of understanding growth rates in algorithms is discussed. By using linear and binary search algorithms as examples, the video illustrates how their performance varies with input size. Linear search becomes extremely slow with large data, while binary search, which operates much faster, shows its efficiency more dramatically as the input grows. The concept of growth rate is explained as the rate at which an algorithm's running time increases with input size. The lecture concludes by introducing Big-O notation as a tool to measure and compare the growth rates of algorithms.

Takeaways

• 😀 Growth rate is essential for analyzing how fast an algorithm works as the input size increases.
• 😀 One example is not sufficient to compare the efficiency of algorithms—growth rate must be considered.
• 😀 Linear search’s running time grows linearly with input size, meaning the time taken increases proportionally with the number of items.
• 😀 Binary search's running time grows logarithmically, which allows it to be much faster for larger input sizes.
• 😀 In the case of 100 items, linear search takes 100 comparisons, while binary search only takes 7 comparisons.
• 😀 For 1 billion items, linear search would take 11 days to process, while binary search only takes 30 milliseconds.
• 😀 Binary search is dramatically faster than linear search, especially as the input size grows larger.
• 😀 Understanding growth rate allows us to make informed decisions about which algorithm to use depending on the problem's scale.
• 😀 The time difference between linear and binary search becomes vast as the size of the data increases—up to 31 million times faster in the case of 1 billion items.
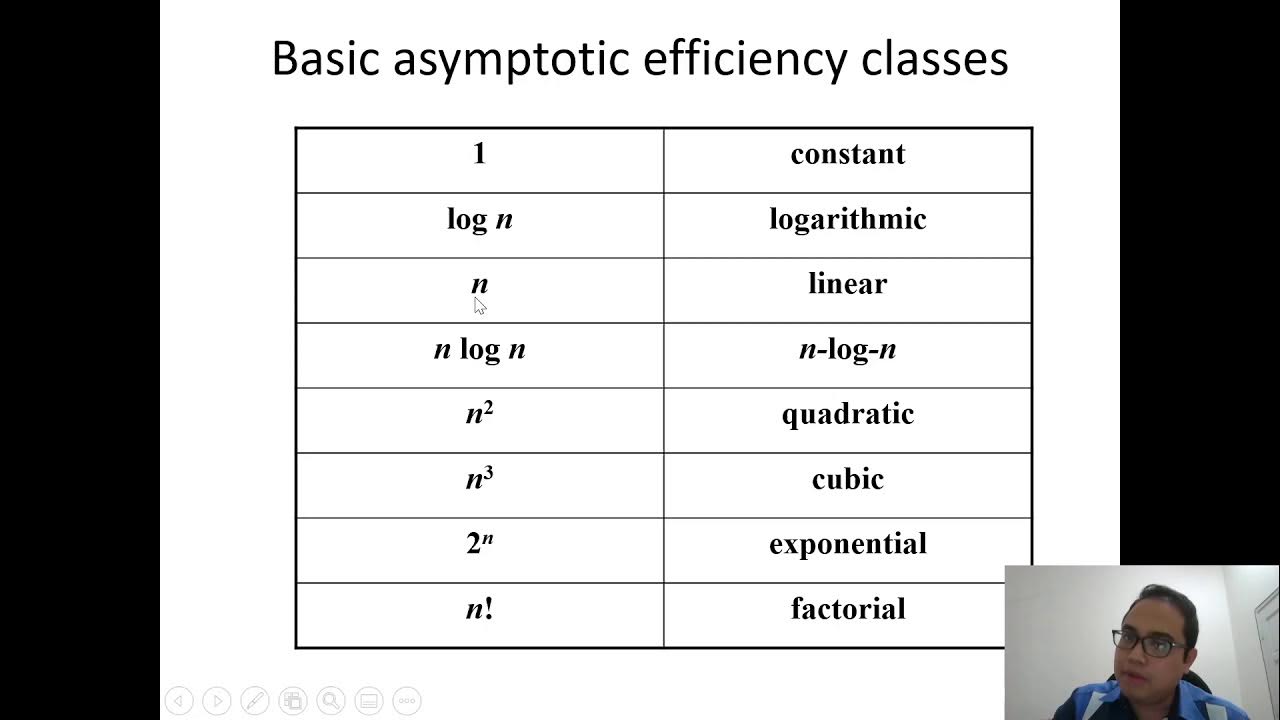
• 😀 To measure the growth rate of an algorithm, Big O notation is used, which will be covered in future lectures.
• 😀 Growth rate provides a quantitative measure of how an algorithm’s performance changes as the size of its input grows.

Q & A

What is the main focus of this lecture?

The main focus of the lecture is understanding the importance of growth rates in analyzing algorithms and why it's crucial for comparing the efficiency of different algorithms as input size increases.

What are the two algorithms compared in this lecture?

The two algorithms compared in this lecture are **linear search** and **binary search**.

How does linear search perform in the example provided?

In the example, with 100 items, linear search requires 100 comparisons to find the key, which takes 100 milliseconds of time in the worst-case scenario.

How does binary search perform in the example with 100 items?

For 100 items, binary search only requires 7 comparisons, taking 7 milliseconds to find the key, making it significantly faster than linear search in this case.

Is binary search always 14 times faster than linear search?

No, binary search is not always 14 times faster. The difference in speed depends on the input size. As the size of the input grows, binary search becomes much faster in comparison to linear search.

What happens when the input size is increased to 1 billion items?

When the input size is increased to 1 billion items, linear search would require 1 billion comparisons, taking 11 days, while binary search only requires 30 comparisons, taking 30 milliseconds. This makes binary search 31 million times faster than linear search in this scenario.

Why is one example not sufficient to compare algorithms?

One example is not sufficient because the performance of an algorithm depends on the input size. To compare algorithms effectively, we need to understand how their performance scales with increasing input sizes.

What is the definition of growth rate in the context of algorithms?

The growth rate refers to the rate at which the running time of an algorithm increases as the input size grows. It helps in understanding how efficiently an algorithm performs as the data set gets larger.

How can we measure the growth rate of an algorithm?

The growth rate of an algorithm can be measured using **Big-O notation**, which expresses the algorithm's efficiency in terms of its input size, allowing for standardized comparison with other algorithms.

Why is Big-O notation important in algorithm analysis?

Big-O notation is important because it allows us to quantify the efficiency of an algorithm and compare it with others based on how the running time increases as the input size grows, regardless of specific execution times or examples.