Distribución normal ejemplo

TutorClass

2 Mar 202006:53

Summary

TLDREste video explora la distribución normal, una forma de probabilidad con forma de campana, caracterizada por su media y desviación estándar. Se discute cómo estandarizar datos utilizando la fórmula Z para calcular probabilidades. A través de un ejemplo práctico, se calcula la probabilidad de que la temperatura en una ciudad sea inferior a 14 grados, concluyendo que la probabilidad es 0.0918. Además, se enseña cómo calcular la probabilidad complementaria para temperaturas superiores a 14 grados, resultando en 0.9082, todo ilustrado gráficamente para facilitar la comprensión.

Takeaways

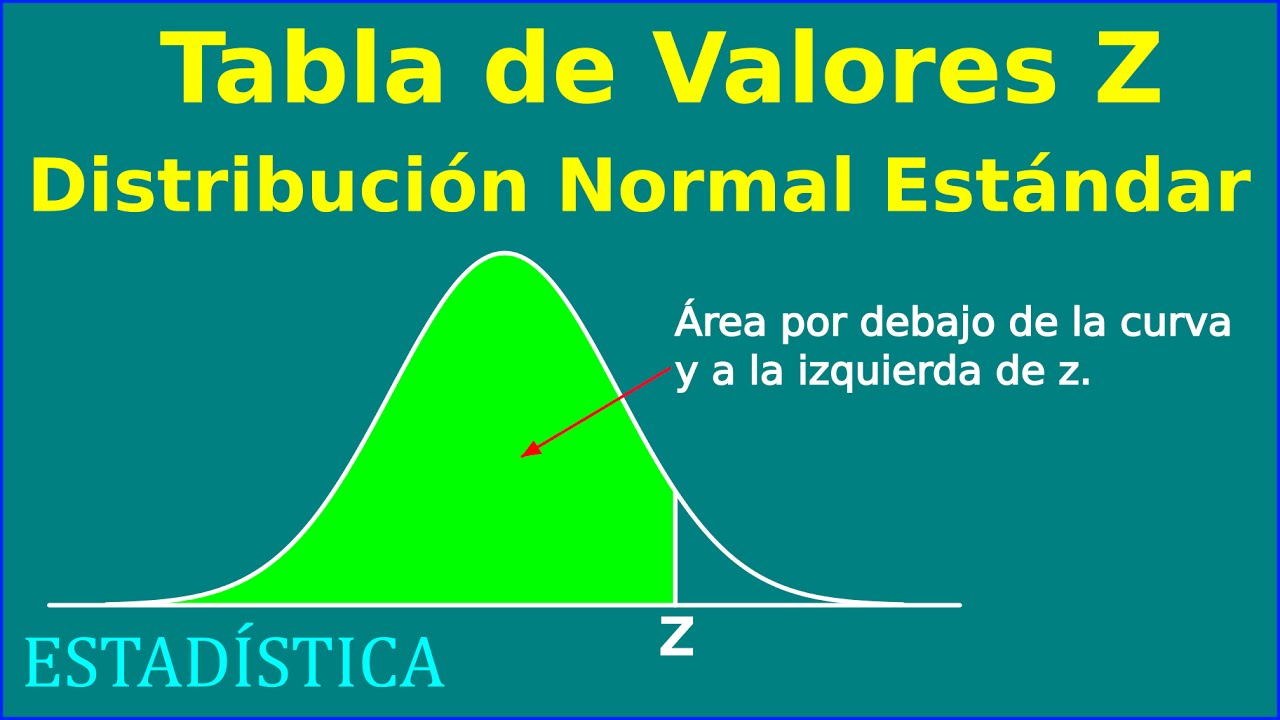
📊 La distribución normal es una distribución de probabilidad que tiene forma de campana, conocida como campana de Gauss.
⚖️ La media (μ) de la distribución normal es simétrica, lo que significa que el 50% de los datos se encuentran a cada lado de la media.
📐 La estandarización se realiza mediante la fórmula z = (x - μ) / σ, donde x es la variable a analizar, μ es la media poblacional y σ es la desviación estándar.
🌡️ Un ejemplo práctico presentado es el cálculo de la probabilidad de que la temperatura en una ciudad sea menor a 14 grados, dada una media de 18 grados y una desviación estándar de 3 grados.
📉 Para calcular la probabilidad de que x sea menor a 14 grados, se utiliza la tabla z para encontrar el valor correspondiente a z = -1.33.
📊 La probabilidad de que la temperatura sea menor a 14 grados se obtiene como 0.0918, lo que representa el área bajo la curva en esa región.
🔄 Si se desea calcular la probabilidad de que la temperatura sea mayor a 14 grados, se utiliza el complemento: P(X > 14) = 1 - P(X ≤ 14).
📈 El resultado del complemento para la probabilidad de que la temperatura sea mayor a 14 grados es 0.9082.
📏 En una distribución normal continua, las probabilidades de menor y menor o igual son equivalentes.
🎨 La presentación gráfica de la distribución normal ayuda a visualizar las áreas de probabilidad, destacando las zonas de interés como la media y los valores extremos.

Q & A

¿Qué es la distribución normal?
-La distribución normal es una distribución de probabilidad que tiene una forma característica de campana, conocida como la campana de Gauss, y es simétrica en torno a su media.
¿Cuáles son las características principales de la distribución normal?
-Las características principales son que su media, representada por 'miu', se encuentra en el centro y es simétrica, lo que significa que el 50% de los datos se encuentra a cada lado de la media.
¿Qué es la estandarización en el contexto de la distribución normal?
-La estandarización es un proceso que permite transformar los datos para que sigan una distribución normal estándar utilizando la fórmula zeta: (X - miu) / sigma.
¿Qué representan 'miu' y 'sigma' en la distribución normal?
-'miu' representa la media poblacional, y 'sigma' representa la desviación estándar de la población.
¿Cómo se calcula la probabilidad de que una variable aleatoria sea menor a un valor específico en una distribución normal?
-Se calcula utilizando la fórmula zeta y luego consultando la tabla z para encontrar la probabilidad asociada a ese valor.
En el ejemplo, ¿cuál es la probabilidad de que la temperatura sea menor a 14 grados?
-La probabilidad de que la temperatura sea menor a 14 grados es de aproximadamente 0.0918, según la tabla z.
¿Qué se entiende por complemento en probabilidad?
-El complemento se refiere a la probabilidad de que ocurra el evento opuesto. En este caso, se utiliza para calcular la probabilidad de que la temperatura sea mayor a 14 grados.
¿Qué valor representa la probabilidad de que la temperatura sea mayor a 14 grados en el ejemplo?
-La probabilidad de que la temperatura sea mayor a 14 grados es aproximadamente 0.9082, que se calcula como 1 menos la probabilidad de que sea menor o igual a 14 grados.
¿Por qué se considera que 'menor' y 'menor o igual' son equivalentes en una distribución continua?
-En una distribución continua, la probabilidad de que un valor sea menor o igual a un número es prácticamente la misma que solo ser menor, ya que la probabilidad de un punto específico es cero.
¿Qué información gráfica se puede obtener sobre la distribución normal en el ejemplo?
-La gráfica muestra la media de la temperatura en 18 grados y el área de probabilidad correspondiente a las temperaturas menores a 14 grados, así como el área que representa las temperaturas mayores a 14 grados.