Distribucion Normal | Ejercicio de Examen #3
Summary
TLDREn este video, el presentador explora problemas de distribución normal, destacando la diferencia entre trabajar con valores Z negativos y positivos. Se explica cómo calcular la probabilidad de una variable aleatoria utilizando la estandarización y la búsqueda de valores en la tabla Z. Con ejemplos prácticos, se muestran los pasos para determinar probabilidades específicas, enfatizando la importancia de entender el proceso de tipificación y la identificación de casos base. Al final, se anima a los espectadores a interactuar y compartir el contenido para ayudar a otros en su estudio de estadística.
Takeaways
- 😀 La tabla de distribución normal utilizada en el video es para valores Z negativos, lo que cambia el enfoque del problema.
- 😀 El caso base ahora es la probabilidad de que la variable Z sea menor o igual que un número negativo.
- 😀 Se utiliza la fórmula P(Z ≤ a) = 1 - P(Z ≤ -a) para calcular probabilidades con valores Z positivos.
- 😀 Para resolver problemas de distribución normal, es crucial tipificar los valores de la variable aleatoria X.
- 😀 La tipificación se realiza utilizando la fórmula Z = (X - media) / desviación estándar.
- 😀 En el primer apartado, se calculó la probabilidad de que la variable X estuviese entre 50 y 85.
- 😀 Los valores de Z correspondientes a 50 y 85 son -1.25 y 0.5, respectivamente.
- 😀 La probabilidad de que Z esté entre -1.25 y 0.5 se calcula como la diferencia de probabilidades de Z en la tabla.
- 😀 En el segundo apartado, se calculó la probabilidad de que la variable aleatoria X fuese menor que 35, resultando en un valor Z de -2.
- 😀 El tercer apartado se centró en calcular la probabilidad de que X estuviese entre 25 y 65, obteniendo valores Z de -2.5 y -0.5.
Q & A
¿Cuál es el objetivo principal del video?
-El objetivo del video es resolver un problema de examen sobre la distribución normal, enfocándose en cómo utilizar la tabla de valores Z para calcular probabilidades.
¿Qué diferencia se menciona respecto a problemas anteriores sobre la distribución normal?
-La diferencia es que en este problema se trabaja con valores de Z negativos, mientras que en los problemas anteriores se utilizaban valores de Z positivos.
¿Cómo se define el caso base en este contexto?
-El caso base es la probabilidad de que la variable Z sea menor o igual que un número negativo, que se consulta directamente en la tabla de valores Z.
¿Cuál es la fórmula utilizada para calcular la probabilidad de que Z sea menor o igual que un valor positivo?
-La fórmula es: P(Z ≤ a) = 1 - P(Z ≤ -a), donde 'a' es el valor positivo que se está considerando.
¿Qué se necesita hacer para calcular la probabilidad de que la variable aleatoria X tome valores entre 50 y 85?
-Se debe tipificar los valores de X = 50 y X = 85, utilizando la fórmula Z = (X - media) / desviación típica.
¿Qué resultados se obtienen al tipificar los valores de 50 y 85?
-Al tipificar 50 se obtiene Z = -1.25 y al tipificar 85 se obtiene Z = 0.5.
¿Cómo se calcula la probabilidad de que Z esté entre -1.25 y 0.5?
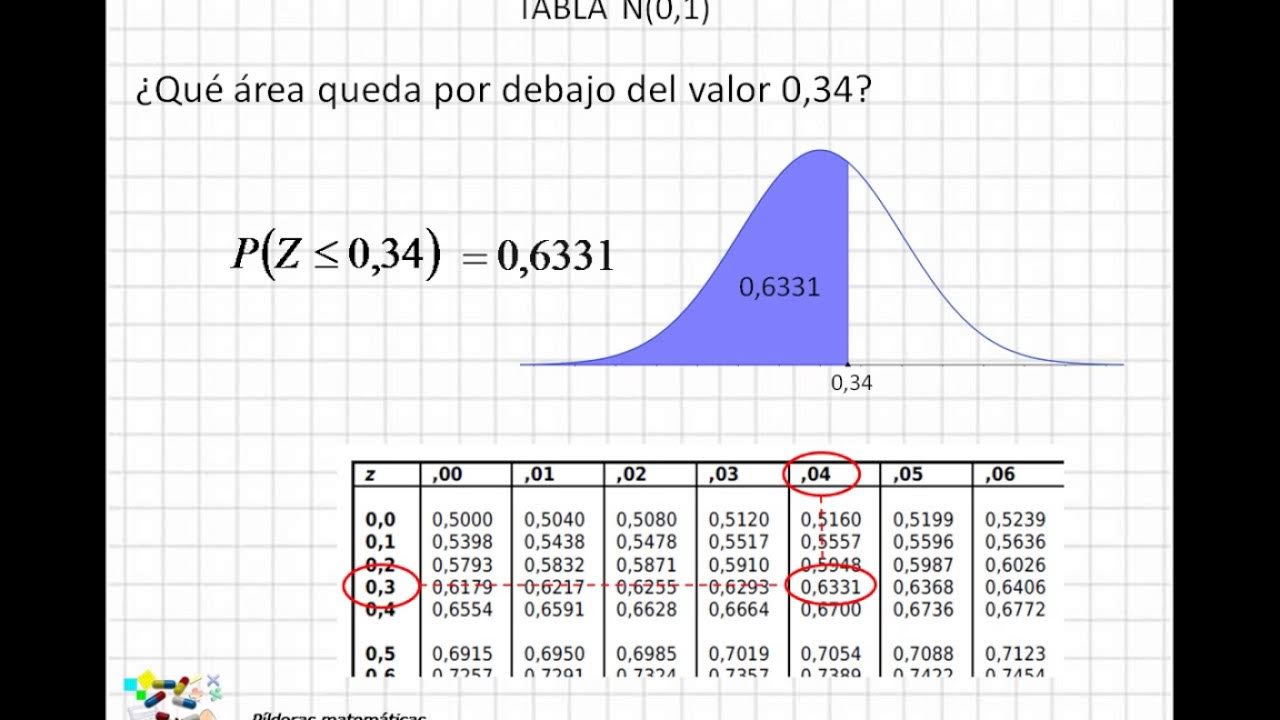
-Se calcula como P(Z ≤ 0.5) - P(Z ≤ -1.25), utilizando la tabla de valores Z para encontrar las probabilidades correspondientes.
¿Qué probabilidad se encuentra en la tabla para Z = -1.25?
-La probabilidad para Z = -1.25 es aproximadamente 0.1056.
¿Cómo se procede si se desea calcular la probabilidad de que la variable aleatoria X sea menor que 35?
-Se tipifica el valor X = 35, que resulta en Z = -2, y se busca P(Z ≤ -2) en la tabla.
¿Qué probabilidad se obtiene al calcular la probabilidad de que Z sea menor que -2?
-La probabilidad para Z = -2, según la tabla, es aproximadamente 0.0228.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)