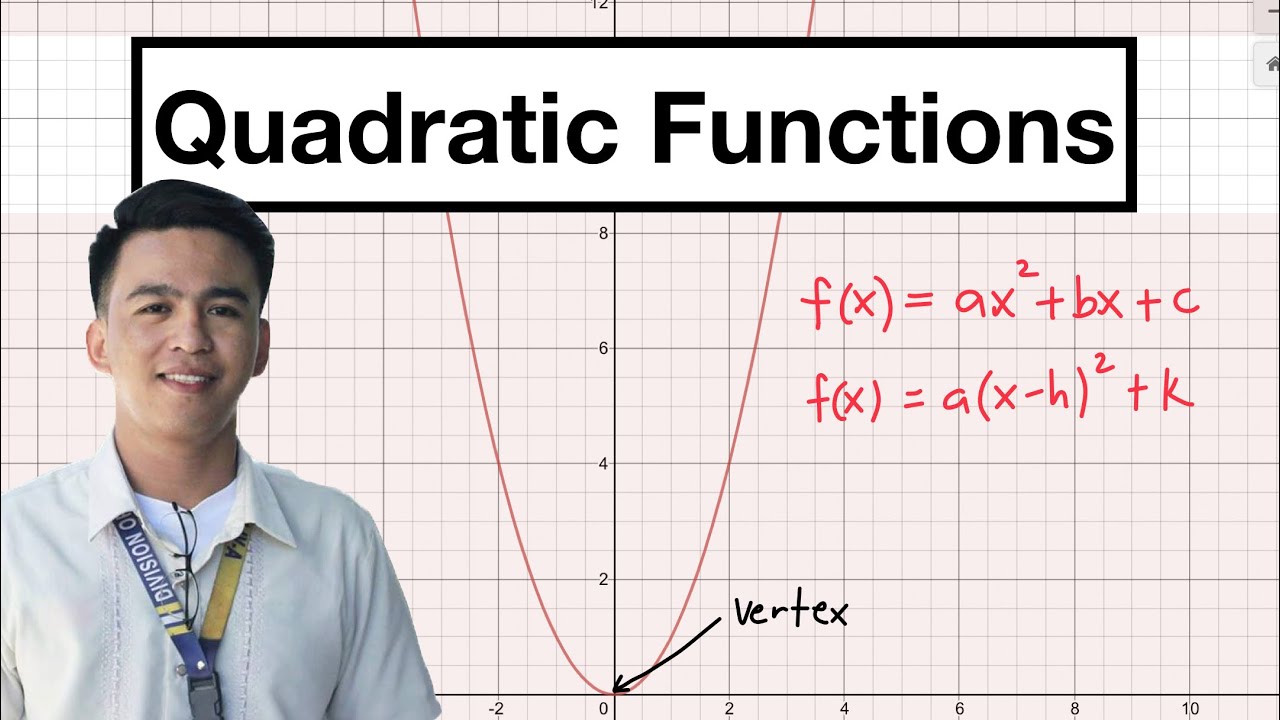
How to Graph Quadratic Functions by finding the Vertex, Axis of symmetry, X & Y intercepts
Summary
TLDRThis lesson teaches how to graph quadratic functions in standard form. It covers the essential steps: determining whether the parabola opens upward or downward, finding the axis of symmetry, vertex, Y intercept, and X intercepts. The process involves using factoring, symmetry, and substituting values into the function. The lesson includes various examples, such as parabolas crossing the X-axis twice, touching the X-axis once, or having no X intercepts at all. By the end, viewers will be equipped to graph quadratic functions with confidence, understanding both simple and more complex cases.
Takeaways
- 😀 A parabola opens upward if 'a' is greater than zero, and downward if 'a' is less than zero.
- 😀 The axis of symmetry of a quadratic function can be found using the formula x = -B / 2A.
- 😀 The vertex's x-coordinate is the same as the axis of symmetry, and the y-coordinate can be found by substituting the x-value into the original function.
- 😀 The Y-intercept occurs when x = 0; substitute x = 0 into the equation to find y.
- 😀 The X-intercepts occur when y = 0. Solve for x using factoring, the quadratic formula, or completing the square.
- 😀 Factoring may not always be straightforward, and sometimes using the quadratic formula or a calculator is necessary to find the X-intercepts.
- 😀 Points on the graph can be found symmetrically across the axis of symmetry for accuracy.
- 😀 It's important to plot at least five points to create an accurate parabola when graphing quadratic functions.
- 😀 In some cases, a quadratic may have only one X-intercept, where the vertex is on the x-axis.
- 😀 A quadratic may have no real X-intercepts if the discriminant is negative, meaning the parabola does not cross the x-axis.
- 😀 Practicing with different quadratic equations, including those that cannot be easily factored, helps improve graphing skills.
Q & A
How do you determine whether a parabola opens upward or downward?
-A parabola opens upward if the coefficient 'a' in the quadratic function is greater than zero. It opens downward if 'a' is less than zero.
What is the formula for finding the axis of symmetry of a quadratic function?
-The formula for the axis of symmetry is x = -B / 2A, where A and B are the coefficients from the standard form of the quadratic function.
How do you find the vertex of a parabola from its equation?
-The x-coordinate of the vertex is the same as the axis of symmetry. To find the y-coordinate, substitute the x-coordinate of the vertex into the original quadratic function.
What is the significance of the y-intercept in a quadratic function?
-The y-intercept occurs when x = 0. It represents the point where the parabola crosses the y-axis.
How do you find the x-intercepts of a quadratic function?
-The x-intercepts occur when y = 0. To find them, set y to zero in the quadratic equation and solve for x, typically by factoring or using the quadratic formula.
What should you do if factoring a quadratic function is difficult or time-consuming?
-If factoring is difficult, you can use the quadratic formula or find other points on the graph to plot the parabola and complete its shape.
What is the role of symmetry in graphing a parabola?
-The parabola is symmetric around the axis of symmetry. For any point on one side of the axis, there is a corresponding point on the other side at an equal distance.
What does it mean when a quadratic function has only one x-intercept?
-A quadratic with only one x-intercept occurs when the vertex lies on the x-axis. This means the parabola touches the x-axis at a single point, which is both the vertex and the intercept.
What happens if the discriminant of a quadratic equation is negative?
-If the discriminant is negative, the quadratic equation has no real solutions, meaning the parabola does not cross the x-axis at all.
How can you make a graph of a quadratic function more accurate?
-You can make the graph more accurate by plotting additional points closer to the axis of symmetry. However, five points are generally enough to plot a decent parabola.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)