Electrical Engineering: Basic Laws (8 of 31) What Are Kirchhoff's Laws?

Summary

This video introduces Kirchhoff's two fundamental laws for analyzing electrical circuits. The first law, Kirchhoff's Current Law (KCL), states that the sum of currents entering a node equals the sum of currents leaving it. The second law, Kirchhoff's Voltage Law (KVL), asserts that the sum of voltages around any closed loop in a circuit must equal zero. The video explains both concepts with examples of current and voltage flows, demonstrating how these principles apply to circuit analysis. Future videos will offer practical examples of using these laws to solve circuits.

Takeaways

• 🔌 Kirchhoff's First Law (KCL) states that the sum of currents entering a node equals the sum of currents leaving the node.
• 🔀 In a circuit, one current may enter a node, while two or more currents leave, and the sum of the outgoing currents equals the incoming one.
• 🚗 The analogy of cars entering and leaving an intersection is used to explain current flow in a node: the number of cars entering must equal the number leaving.
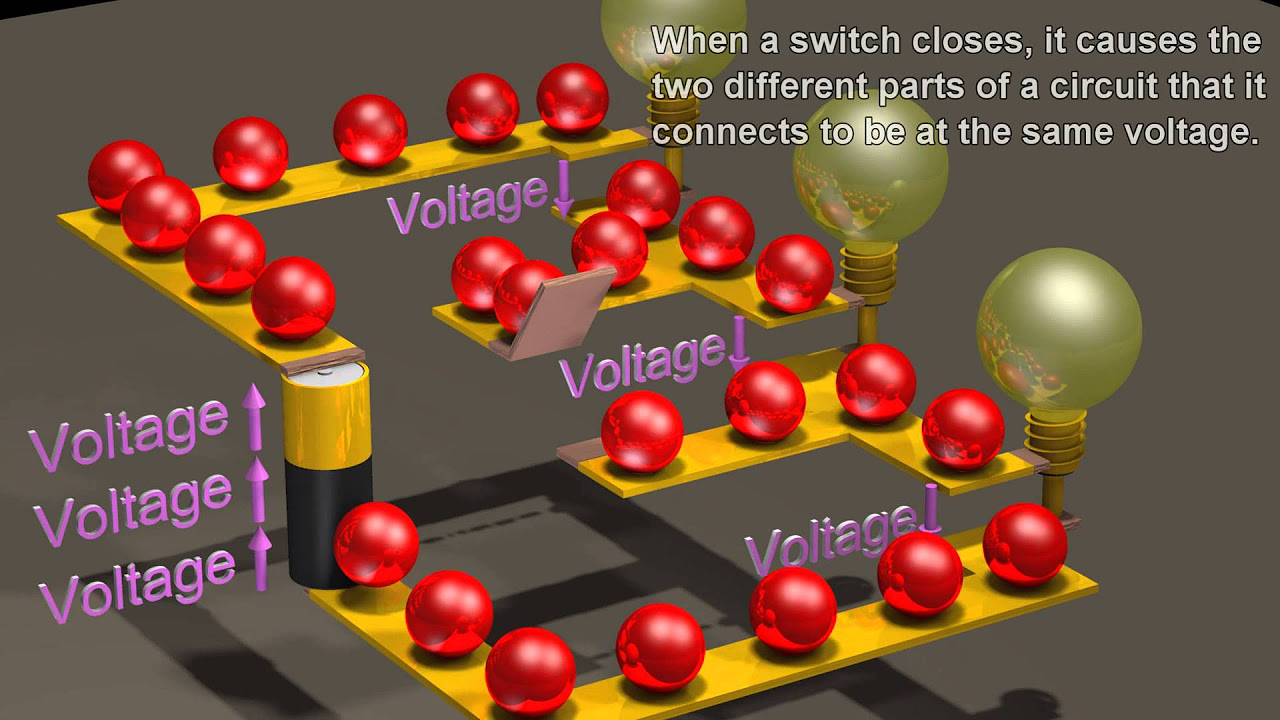
• 🔋 Kirchhoff's Second Law (KVL) states that in any closed loop, the sum of all voltages (voltage rises and drops) must equal zero.
• ⬆️ When moving across a battery from the negative to positive terminal, there's a positive voltage rise.
• 🔻 When current flows through a resistor in the same direction as the loop, it results in a voltage drop.
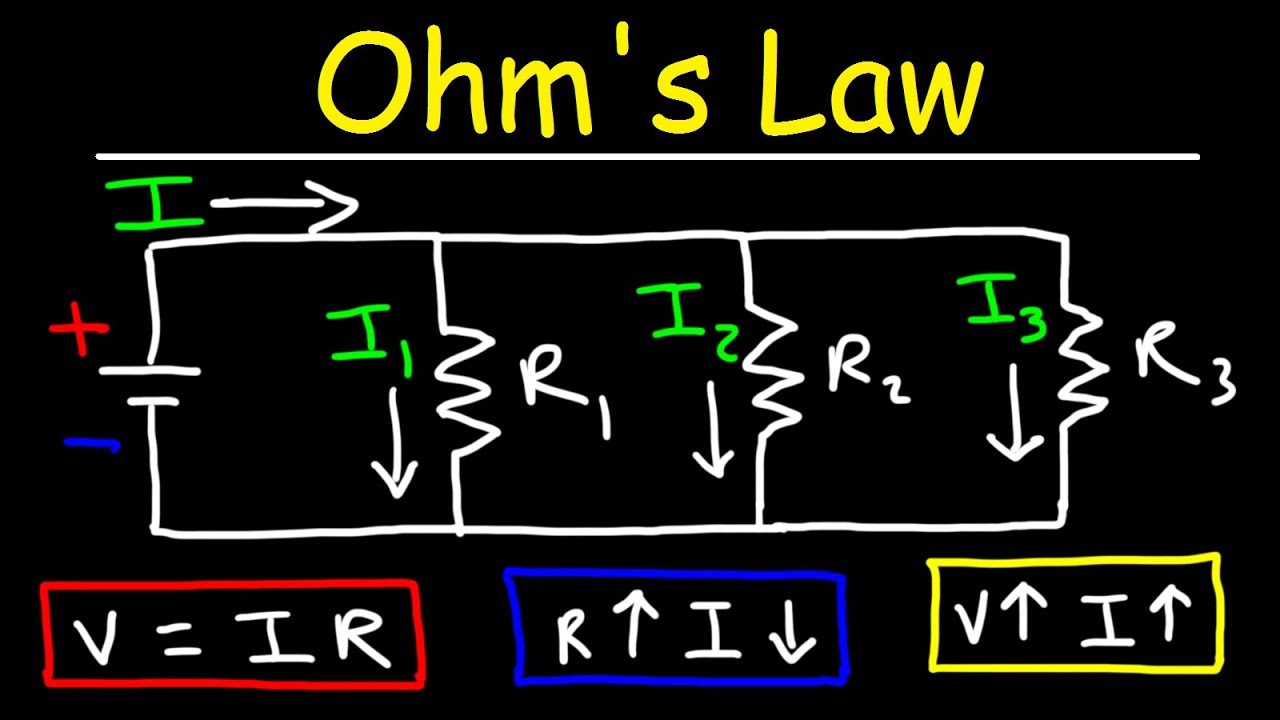
• 🔄 The voltage across a resistor is determined by the current through it and the resistor's resistance (Ohm's Law: V = IR).
• ⏩ The direction of travel in a loop relative to the current determines whether there is a voltage rise or drop across a resistor.
• 🔁 Traveling in the opposite direction of current through a resistor results in a voltage rise, not a drop.
• 💡 The two Kirchhoff laws (KCL and KVL) are essential tools for analyzing electrical circuits by balancing currents and voltages in nodes and loops.

Q & A

What is Kirchhoff's first law?

Kirchhoff's first law, also known as the Current Law, states that for any node, the sum of all currents entering the node equals the sum of all currents leaving the node. This principle is based on the conservation of charge.

Can you provide an example of Kirchhoff's first law?

In a circuit with three branches connected to a node, if current I1 enters the node and currents I2 and I3 leave the node, Kirchhoff's first law states that I1 = I2 + I3. This ensures that the total current entering the node equals the total current leaving it.

What analogy is used to explain Kirchhoff's first law?

An analogy of cars at an intersection is used. The number of cars entering the intersection must equal the number of cars leaving, unless the cars disappear. Similarly, the currents entering and leaving a node must be equal.

What does Kirchhoff's second law state?

Kirchhoff's second law, also known as the Voltage Law, states that for any closed loop in a circuit, the sum of all the voltages (voltage rises and voltage drops) must add up to zero. This is based on the conservation of energy.

How does the direction of current affect the voltage across a resistor?

When traveling in the same direction as the current across a resistor, a voltage drop occurs, and it's considered negative. When traveling in the opposite direction of the current, a voltage rise occurs, and it's considered positive.

How do you calculate the voltage drop across a resistor?

The voltage drop across a resistor is calculated using Ohm's Law, which is the current (I) in the circuit multiplied by the resistance (R) of the resistor, i.e., V = I * R.

What happens when you travel around a closed loop in a circuit?

As you travel around a closed loop, the sum of all voltage rises and voltage drops must equal zero. This is in line with Kirchhoff's second law.

Why must the sum of voltages around a closed loop equal zero?

The sum of voltages must equal zero because energy is conserved. As you move through the circuit, energy gained from sources (like batteries) must be equal to the energy lost across resistors or other components.

How do you handle voltage when traveling in the same direction as the current?

When traveling in the same direction as the current, the voltage across a resistor is a drop, and this is counted as a negative value in Kirchhoff's voltage law.

What is the importance of understanding the direction of current in Kirchhoff's laws?

Understanding the direction of current is crucial to applying Kirchhoff's laws correctly, especially when determining whether to add or subtract voltages in a loop and correctly interpreting current flows in and out of nodes.

Outlines

00:00

⚡ Understanding Kirchhoff's Current Law (KCL)

This paragraph introduces Kirchhoff's Current Law (KCL), which states that for any electrical node, the sum of currents entering the node must equal the sum of currents leaving it. The example provided illustrates this concept using a node with three resistors, where one current (I1) enters and two currents (I2 and I3) leave. The idea is compared to cars entering and leaving an intersection, emphasizing that the sum must balance unless charges disappear. Therefore, I1 equals the sum of I2 and I3, which is a fundamental principle in circuit analysis.

05:00

🔋 Exploring Kirchhoff's Voltage Law (KVL)

This paragraph introduces Kirchhoff's Voltage Law (KVL), which states that in any closed loop of an electrical circuit, the sum of all voltages (voltage rises and drops) must equal zero. The explanation uses a simple loop with a battery and resistors, showing how voltage rises across a battery and drops across resistors. The voltage drop across a resistor is proportional to the current flowing through it and its resistance. In this way, the total voltage in the loop (source voltage minus the resistor drops) must add up to zero.

🔄 Voltage Drops and Rises in Circuit Loops

This paragraph explains how voltage changes across a resistor depending on the direction of travel in relation to the current flow. When traveling in the same direction as the current, there is a voltage drop, and when traveling in the opposite direction, there is a voltage rise. This distinction is crucial when calculating voltages around a loop, as traveling in different directions can affect whether the voltage is added or subtracted in the equation for the loop's total voltage.

📚 Summary of Kirchhoff's Laws and Applications

The final paragraph summarizes the two key Kirchhoff's laws: the Current Law, which states that the sum of currents entering a node equals the sum of currents leaving it, and the Voltage Law, which dictates that the sum of voltages in any closed loop must equal zero. These laws are powerful tools for analyzing circuits, and the following videos will provide examples of their practical application in solving circuit problems.

Keywords

💡Kirchhoff's Laws

Kirchhoff's Laws consist of two fundamental principles for analyzing electrical circuits: Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL). These laws are central to understanding the behavior of electrical currents and voltages in any circuit, and are used extensively in circuit analysis. The video focuses on explaining both of these laws and their practical applications.

💡Node

A node in an electrical circuit is a point where two or more circuit elements, such as resistors or wires, are connected. Kirchhoff's Current Law (KCL) applies to nodes by stating that the sum of currents entering and leaving a node must be equal. In the video, a node is used as an example where currents are entering and leaving, showing how KCL is applied to analyze the circuit.

💡Current

Current refers to the flow of electric charge in a circuit. In the context of Kirchhoff’s Current Law (KCL), the video explains how the currents entering and leaving a node must balance out. Current is denoted by symbols such as I1, I2, and I3 in the video’s example, and is shown to either enter or exit a node in a circuit.

💡Resistor

A resistor is a component in an electrical circuit that resists the flow of current, causing a voltage drop. The video mentions resistors in the context of analyzing voltage drops across them, with the voltage being proportional to the current through the resistor. The resistance is denoted by R1 and R2 in the video.

💡Voltage

Voltage is the electrical potential difference between two points in a circuit. Kirchhoff’s Voltage Law (KVL) deals with the sum of all voltages in a closed loop, which must equal zero. In the video, voltage is discussed in the context of both voltage rises and drops, and how they balance out in a circuit loop.

💡Closed Loop

A closed loop in an electrical circuit is a complete path through which current can flow without interruption. According to Kirchhoff’s Voltage Law (KVL), the sum of all voltages in a closed loop must equal zero. The video uses the concept of a closed loop to explain how voltage rises and drops are calculated as one travels around the circuit.

💡Voltage Drop

A voltage drop occurs when electrical energy is lost as it passes through a resistor or other component in a circuit. In the video, voltage drops are associated with resistors, and the voltage drop across each resistor is equal to the current multiplied by the resistor’s value (I * R). Voltage drops are subtracted when calculating the total voltage around a loop.

💡Voltage Rise

A voltage rise refers to an increase in electrical potential as one moves across a component, typically a power source like a battery. In the video, a voltage rise is shown when moving from the negative to the positive terminal of a battery. Voltage rises are added in the calculation of total voltage around a closed loop.

💡Current Direction

Current direction refers to the flow of electric charge in a specific direction through a circuit. The video emphasizes the importance of understanding current direction when applying Kirchhoff’s Voltage Law (KVL), as the direction of travel in relation to current determines whether you experience a voltage rise or drop.

💡Battery

A battery is a source of electrical energy in a circuit that provides a voltage rise. In the video, the battery is used as an example of a component that causes a positive voltage when moving from its negative to positive terminal. It is an essential element in creating a voltage difference that drives current through the circuit.

Highlights

Introduction to Kirchhoff's laws: Two fundamental laws that help analyze electrical circuits.

Kirchhoff's first law (Current Law): The sum of all currents entering a node equals the sum of all currents leaving the node.

Example of Kirchhoff's current law: A node with one entering current (I1) and two leaving currents (I2 and I3). The equation I1 = I2 + I3 demonstrates the rule.

Analogy for current flow: Similar to cars at an intersection—the number of cars entering must equal the number of cars leaving.

Kirchhoff’s second law (Voltage Law): For any closed loop in a circuit, the sum of all voltages (both rises and drops) must equal zero.

Example of Kirchhoff's voltage law: Starting at one node and traveling around a closed loop, the voltage rises across a battery and voltage drops across resistors must balance to zero.

The voltage across a resistor: Calculated as the current (I) multiplied by the resistance (R), represented as V = I * R.

Application of Kirchhoff's voltage law: The sum of the voltage rise across the battery minus the voltage drops across two resistors equals zero.

Understanding voltage drops and rises: Voltage drops occur when traveling with the current direction, while voltage rises occur when traveling opposite to the current direction.

Directional effect on voltage: If traveling in the same direction as the current across a resistor, a voltage drop is experienced; if traveling in the opposite direction, a voltage rise is experienced.

Significance of analyzing loops: The direction of travel in a loop affects whether voltage across components is added or subtracted.

Practical implications: These two laws (current and voltage) are essential for analyzing electrical circuits.

Kirchhoff's current law is crucial for analyzing nodes, while the voltage law is used for analyzing closed loops in circuits.

The combination of Kirchhoff's laws: Allows for solving complex electrical circuits by applying both current and voltage laws.

Conclusion: Kirchhoff's laws are powerful tools in electrical circuit analysis, allowing for systematic approaches to current and voltage calculations.

Transcripts

welcome to electure online in this video

we're going to explore kirov laws there

are two kirov laws the first one says

that for any node the sum of all the

currents entering the node equal the sum

of all the currents leaving the node in

this example let's say we have this node

we have one two three resistors all

three sharing the node we have current

flowing in this direction on this

particular across this particular Branch

let's call it i1 we have a current

across this Branch let's call it I2 and

a current across this Branch let's call

it

I3 notice that in this case there's only

one current that is entering this node

it comes from this direction it's i1

that enters the node and there's two

currents that are leaving the node just

like you can stand on any intersection

watch of the number of cars entering the

intersection and watch of the number of

cars leaving the intersection the number

of cars entering must always equal the

number of cars leaving unless they

somehow disappear

same with charges and therefore same

with currents in this case we can say

that the number of currents enter the

node which is i1 must equal the two the

two currents the sum of the two currents

leaving the node therefore we can say i1

equal I2 + I3 and this is an equation

that simply stems from the fact that

kirkov said that all the currents

entering the node equals all the

currents leaving the node which is

indeed a fact now the second rule is has

to do with

voltages kirkov said that if you travel

across or around any closed loop from

any starting point ending at the same

starting point for any Loop all the

voltages added together must add up to

zero now when we say all the voltages

added together that means all the

voltage Rises and all the voltage drops

in this case since we're traveling with

the current let's say we start from this

node we cross the battery from the

negative end to the positive end we then

sum up this voltage we have a positive

voltage here traveling from the negative

end to the positive end we then travel

across this resistor that would be a

voltage drop we travel across this

resistor that would be a voltage drop

remember the voltage across any resistor

is equal to the current in the circuit

in this case I times the size of the

resistor in this case R1 and R2 so the

sum of all the voltages starting from

this note right here is equal to the

volts across the source minus the

voltage drop across the resistor which

is the current times the first resistor

minus the voltage drop across the second

resistor which is I * R2 and that

therefore must add up to zero because

CRA rule says you add up all the

voltages as you travel around any given

Loop any Clos Loop they must always add

up to

zero to get a better feel for what

happens across the resistor it does

depend what direction you travel

relative to the current for example

let's say that we're traveling around

the loop we're traveling in this

direction from left to right across the

resistor which happens to be the same

direction as the current flow in that

particular Branch therefore we

experience what we call a voltage drop

the voltage is higher on the left side

as it is compared to the right side of

this Branch therefore when we travel

around the loop in that direction we

have a voltage drop and so we call that

a negative voltage however if we travel

in the opposite direction let's say we

go around the loop in the opposite

direction we're traveling from right to

left but the current flows from left to

right so now we're traveling in the

opposite direction of the current when

we travel across the resistor we

experience a voltage rise we know that

the voltage is higher on this side as it

is compared to this side the left side I

should say the right side therefore when

we travel from the negative end of the

resistor to the ne to the positive end

meaning that the potential or the

voltage is higher here compared to here

we travel in this direction we see a

voltage rise and then we would have to

add a positive voltage instead of a

negative voltage in the next several

videos we'll do some examples of how to

deal with K kirkov rules and laws in

this case you can see that you do have

to take uh be careful when you go around

the loop to see if the direction of

travel around the loop is in the same

direction the current or in the opposite

direction to determine if you should add

the the voltage or or subtract the

voltage across that particular divis or

across that particular Branch again in

summary the two laws are for any node

the sum of the currents entering the

node must equal the sum of the currents

leaving the node and the second law for

any Loop for any closed loop I should

call it closed loop it's implied that

it's a closed loop but just in case

you're wondering for any closed loop

when you go all the way around the loop

and you add up all the voltage as you

travel around the loop the sum of all

the voltages must add up to zero those

two rules are very powerful rules which

we can use to analyze all kinds of

circuits so we'll show you some examples

in the videos to come