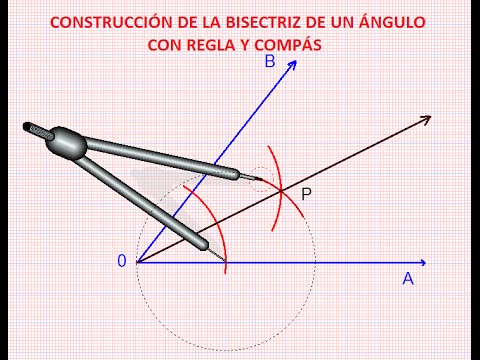
ángulos adyacentes

kpitang mate

9 Apr 202104:12

Summary

TLDREl vídeo explica qué son los ángulos adyacentes, destacando que deben compartir el mismo vértice y un lado común entre dos lados no comunes. Se ilustra con ejemplos cómo los ángulos 'a' y 'b' son adyacentes, mientras que otros como 'a' y 'b' no lo son debido a que no comparten el vértice. Se enfatiza la importancia de diferenciar entre ángulos adyacentes y otros tipos de ángulos para evitar confusiones geométricas.

Takeaways

🔍 Los ángulos adyacentes son aquellos que comparten el mismo vértice y un lado común entre dos lados no comunes.
📐 Se identifican los ángulos adyacentes usando letras, donde la letra en medio indica el vértice compartido.
⚠️ Los ángulos que solo comparten un lado pero no tienen el mismo vértice no son considerados adyacentes.
📌 La letra 'd' en notación matemática a veces se usa para señalar el vértice compartido.
👉 Los ángulos deben compartir el vértice y el lado interno entre los no comunes para ser adyacentes.
🚫 Los ángulos que comparten el lado externo no pueden ser adyacentes ni co-lineales.
📝 Se enfatiza la importancia de distinguir entre ángulos que solo comparten un lado y aquellos que son verdaderamente adyacentes.
📑 El vídeo proporciona ejemplos gráficos para ilustrar la diferencia entre ángulos adyacentes y no adyacentes.
📐 Se explica que para que dos ángulos sean adyacentes, deben cumplir con la condición específica de compartir vértice y lado interno.
🎯 El vídeo finaliza con una recapitulación de que los ángulos adyacentes tienen que compartir el vértice y el lado entre los no comunes.

Q & A

¿Qué son los ángulos adyacentes?
-Los ángulos adyacentes son aquellos que comparten el mismo vértice y tienen un lado común entre ellos que no es compartido por otros ángulos.
¿Cuál es la condición necesaria para que dos ángulos sean considerados adyacentes?
-Dos ángulos son adyacentes si tienen el mismo vértice y comparten un lado que está entre ellos y no es común con otros ángulos.
¿Por qué no son adyacentes los ángulos que comparten solo un lado?
-Los ángulos que comparten solo un lado pero no tienen el mismo vértice no son adyacentes, ya que la definición de ángulos adyacentes requiere que también compartan el vértice.
¿Cuál es la diferencia entre un lado común y un lado no común en la definición de ángulos adyacentes?
-Un lado común en la definición de ángulos adyacentes es el que está entre ellos y no es compartido por otros ángulos. Un lado no común es cualquier otro lado que no forme parte de la relación adyacente entre los dos ángulos.
¿Cómo se identifican los ángulos adyacentes en una representación gráfica?
-En una representación gráfica, los ángulos adyacentes se identifican por compartir el mismo vértice y tener un lado que los une directamente, sin que otros ángulos intervengan en ese lado.
¿Qué sucede si dos ángulos comparten un lado pero no tienen el mismo vértice?
-Si dos ángulos comparten un lado pero no tienen el mismo vértice, no son adyacentes. La condición de compartir el vértice es esencial para que sean considerados adyacentes.
¿Cómo se diferencian los ángulos adyacentes de los ángulos que son simplemente consecutivos en una figura?
-Los ángulos adyacentes son consecutivos y además comparten el mismo vértice y un lado común. Mientras que ángulos consecutivos pueden no compartir vértice ni lado común.
¿Es posible que dos ángulos adyacentes no sean co-lineales?
-No, dos ángulos adyacentes siempre son co-lineales porque comparten un lado común que está entre los no comunes, lo que significa que están alineados en una sola línea.
¿Cuál es la importancia de entender la diferencia entre ángulos adyacentes y no adyacentes en matemáticas?
-La importancia de entender la diferencia radica en la precisión en la definición y el cálculo de propiedades geométricas, como el ángulo interior y exterior, así como en la resolución de problemas geométricos.
¿Cómo se pueden usar los conceptos de ángulos adyacentes en la enseñanza de la geometría?
-Los conceptos de ángulos adyacentes pueden usarse para enseñar la relación entre ángulos en figuras geométricas, ayudar a los estudiantes a identificar y analizar patrones y propiedades en la geometría plana.