Métodos Numéricos: Método de BISECCIÓN, y colocación e interpretación gráfica.
Summary
TLDREl vídeo explica el método de la disección, un sencillo y poderoso método numérico para encontrar las raíces de una ecuación. Se describe cómo elegir valores iniciales y cómo usar el cambio de signo en los valores de la función para determinar la existencia de raíces. Se detalla el proceso iterativo de evaluación y ajuste de intervalos para aproximar la raíz, incluyendo cómo detenerse basándose en el error absoluto o un número fijo de iteraciones.
Takeaways
- 📐 El método de la bisección es un método numérico sencillo para encontrar la raíz de una ecuación.
- 🔍 Se inicia con la bisección en cualquier curso de métodos numéricos debido a su utilidad y facilidad de uso.
- 🌐 La raíz de una ecuación se encuentra cuando la gráfica intersecta el eje X, que representa la variable independiente.
- 📈 Para aplicar la bisección, se eligen dos valores iniciales que encierran a la raíz y se evalúa la función en esos puntos.
- 📉 La clave del método es observar el cambio de signo en los valores evaluados, ya que indica la presencia de una raíz en el intervalo.
- 📊 Se pueden usar herramientas de gráficas como Excel para ayudar en la selección de los valores iniciales.
- 🔢 Se evalúa la función en el punto medio del intervalo para determinar si se debe cambiar el límite superior o inferior.
- ➗ El proceso se repite iterativamente, ajustando el intervalo y evaluando en el punto medio hasta alcanzar la precisión deseada.
- 🔄 Se detendrá el proceso cuando el error absoluto sea menor que un umbral establecido o después de un número fijo de iteraciones.
- ✋ Es importante entender las bases matemáticas antes de aplicar el método de la bisección para evitar errores.
Q & A
¿Qué es el método de la disección en matemáticas?
-El método de la disección es un método numérico sencillo y poderoso para encontrar la raíz de una ecuación, es decir, el punto donde la gráfica de la función intersecta el eje X.
¿Cómo se inicia el método de la disección?
-Se inicia eligiendo dos valores iniciales, generalmente límites superior e inferior, que encierran a la raíz de la ecuación.
¿Por qué es importante que los valores iniciales encierren a la raíz?
-Es crucial para asegurar que la raíz que se busca esté entre estos valores, ya que el método se basa en la intersección de la gráfica con el eje X dentro de ese intervalo.
¿Qué significa que la función cambie de signo?
-Un cambio de signo en los valores de la función evaluada en los límites del intervalo indica que hay al menos una raíz en el intervalo.
¿Cómo se evalúa si hay más de una raíz en el intervalo?
-Si la función cambia de signo más de una vez en el intervalo, puede haber múltiples raíces.
¿Qué es la fórmula para calcular el nuevo valor medio en el método de la disección?
-La fórmula es (x_l + x_r) / 2, donde x_l es el límite inferior y x_r es el límite superior del intervalo actual.
¿Qué se hace si el resultado de la función evaluada en el nuevo valor medio es cero?
-Si el resultado es cero, entonces el nuevo valor medio es la raíz y el proceso se termina.
¿Cómo se decide cuándo detener el proceso del método de la disección?
-Se puede detener el proceso cuando el error absoluto es menor que un umbral dado, como un 0.1%, o después de un número fijo de iteraciones.
¿Qué es el error absoluto en el contexto del método de la disección?
-El error absoluto se refiere a la diferencia absoluta entre el valor actual de x_r y el valor anterior, y se puede usar para medir la precisión del método.
¿Cuál es la importancia de graficar la función antes de aplicar el método de la disección?
-Graficar la función ayuda a seleccionar los valores iniciales adecuados y a entender visualmente la distribución de las raíces.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
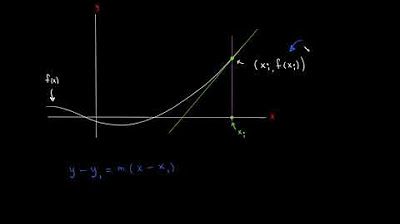
Métodos Numéricos: Newton Raphson

RESOLVER SISTEMAS DE ECUACIONES MÉTODO DE REDUCCIÓN O SUMA Y RESTA Super fácil - Para principiantes

Ecuación de Van der Waals (Volumen - Newton Raphson)

Sistemas de ecuaciones lineales 2x2 | Método de Sustitución | Ejemplo 1

RAÍCES DE UN POLINOMIO │Ejercicio 1
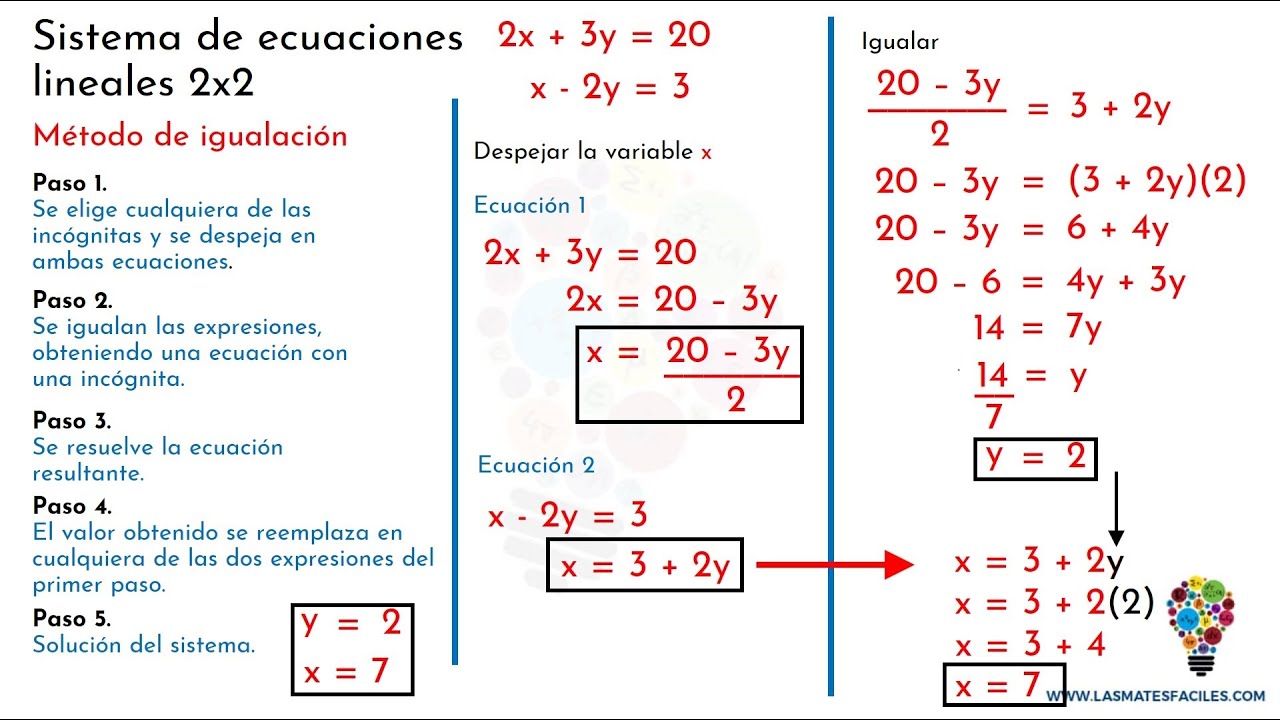
Sistemas de Ecuaciones 2x2 - Método de Igualación
5.0 / 5 (0 votes)
