How To Know Which Statistical Test To Use For Hypothesis Testing
Summary
TLDRThis lecture aims to demystify the selection of appropriate statistical tests for undergraduate students, addressing the common confusion over when to use each test. The instructor lists and explains various tests including one-sample z-tests and t-tests for both means and proportions, two-sample independent tests, matched or paired sample tests, chi-squared tests, regression tests, and one-way ANOVA tests. The focus is on understanding the purpose of each test to determine statistical significance in different scenarios, such as comparing sample means to a known average or examining the impact of treatments in experiments.
Takeaways
- 📚 The lecture introduces various statistical tests typically taught in undergraduate statistics classes.
- 🤔 Students often struggle to determine which statistical test to use, prompting the need for guidance on their appropriate applications.
- 📊 The one-sample z-test and t-test for the mean are used to compare a sample mean to a known population mean, with a t-test being more reliable.
- 📈 The one-sample z-test and t-test for proportions are used for comparing sample proportions to known population proportions, with a focus on qualitative variables.
- ⚖️ Two-sample independent tests for the mean and proportions are employed to compare averages or proportions between two different groups, such as control and treatment groups in an experiment.
- 🔗 Matched or paired sample tests are used when the same group of subjects is measured twice, such as pre- and post-tests, to determine if there's a significant change.
- 📊 Chi-squared tests are designed to assess the relationship between two qualitative variables, which cannot be easily graphed due to their binary nature.
- 📈 Regression tests are used to measure the correlation or association between two quantitative variables, helping to understand how changes in one variable may affect another.
- 🧪 One-way ANOVA tests extend the concept of the two-sample t-test to compare the means of three or more groups, useful for analyzing the effect of multiple treatments.
- 📝 The lecture emphasizes the importance of understanding when to use each test to avoid incorrect conclusions in statistical analysis.
Q & A
What is the main purpose of the lecture discussed in the transcript?
-The main purpose of the lecture is to introduce various statistical tests typically covered in undergraduate statistics classes and to explain when to use each test.
What are the two types of one-sample tests mentioned for the mean in the transcript?
-The two types of one-sample tests mentioned for the mean are the one-sample z-test and the one-sample t-test.
Why does the lecturer suggest avoiding the use of z-tests?
-The lecturer suggests avoiding z-tests because they make assumptions that are often not valid, and they are generally less reliable than t-tests.
What is the difference between a mean and a proportion in the context of statistical tests?
-A mean is used for quantitative variables and represents the average of a set of numbers, while a proportion is used for qualitative variables and represents the ratio of a particular characteristic within a group.
What is the purpose of the one-sample z-test for proportions?
-The one-sample z-test for proportions is used to determine if the proportion of a certain characteristic in a sample is statistically different from the proportion believed to exist in the population.
What are the two independent sample tests for the mean used for?
-The two independent sample tests for the mean are used to determine if there is a statistically significant difference between the means of two separate groups, such as a control group and a treatment group in an experiment.
How does the two-sample independent test for proportions differ from the test for the mean?
-The two-sample independent test for proportions is used for qualitative variables to determine if there is a significant difference in proportions between two groups, whereas the test for the mean is used for quantitative variables.
What is the key difference between paired sample tests and independent sample tests?
-Paired sample tests involve the same group of subjects measured twice (e.g., before and after an intervention), whereas independent sample tests involve two separate groups that are not related to each other.
What does the chi-squared test help to determine in the context of statistical analysis?
-The chi-squared test helps to determine if there is a relationship between two qualitative variables by analyzing the observed frequencies in a contingency table against expected frequencies.
What is the one-way ANOVA test used for, as explained in the transcript?
-The one-way ANOVA test is used to determine if there are statistically significant differences between the means of three or more independent groups.
Why might a researcher use regression tests in their statistical analysis?
-A researcher might use regression tests to measure the degree of association or correlation between two quantitative variables to understand how changes in one variable are related to changes in another.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Common Statistical Tools: Preliminary Concepts
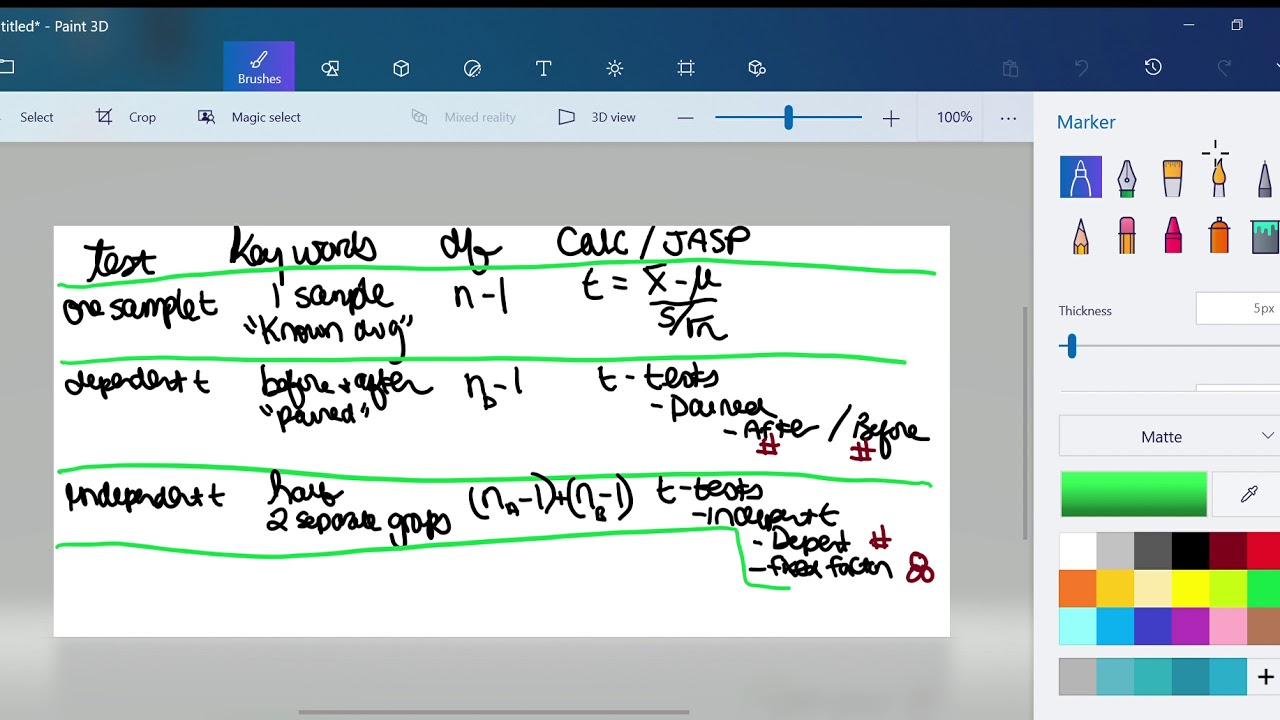
Review of t tests and ANOVA

Statistika Parametrik atau Nonparametrik? || Memilih jenis uji dan syarat uji parametrik
T-test, ANOVA and Chi Squared test made easy.

How to choose an appropriate statistical test

Perbedaan Statistika Parametrik dan Non Parametrik
5.0 / 5 (0 votes)
