✅DISTANCIA y PUNTO MEDIO | APRÉNDELO HOY FÁCIL 💯| GEOMETRÍA ANALÍTICA
Summary
TLDREn este vídeo de geometría analítica, se explora el cálculo de la distancia y el punto medio en el plano cartesiano. Se presentan dos fórmulas clave: una para determinar la distancia entre dos puntos y otra para encontrar el punto medio de un segmento. A través de un ejercicio práctico, se calculan los puntos medios y el perímetro total de un triángulo cuyo vértices están dados. El vídeo guía paso a paso a través de las operaciones matemáticas, incluyendo la simplificación de radicales y la suma de distancias para obtener el perímetro.
Takeaways
- 📐 La distancia en el plano cartesiano se calcula usando la fórmula derivada del teorema de Pitágoras.
- 📍 Para encontrar el punto medio entre dos puntos, se utiliza la fórmula del promedio de las coordenadas x e y.
- 🔢 La fórmula de distancia proporciona una medida en unidades, mientras que el punto medio da una coordenada específica.
- 📈 Se ejemplifica con una línea horizontal en el plano cartesiano para explicar la distancia y el punto medio.
- 📌 Se describe un ejercicio práctico que involucra la identificación de los vértices de un triángulo en el plano cartesiano.
- 📝 Se calcula el punto medio de cada lado del triángulo utilizando la fórmula de promedio de coordenadas.
- 📖 Se explica que el cálculo del perímetro total del triángulo requiere la aplicación de la fórmula de distancia.
- 🧮 Se detalla el proceso de cálculo de la distancia entre los vértices del triángulo, utilizando la fórmula de distancia.
- 🔄 Se menciona la importancia de racionalizar las expresiones radicales para simplificar los cálculos.
- 📉 Se destaca que la suma del perímetro total del triángulo puede ser resuelta fácilmente con una calculadora para obtener un valor decimal.
Q & A
¿Cuál es el tema principal del vídeo de geometría analítica?
-El tema principal del vídeo es la distancia y el punto medio en el plano cartesiano.
¿De qué manera se deriva la fórmula para calcular la distancia en el plano cartesiano?
-La fórmula para la distancia se deriva del teorema de Pitágoras.
Si un segmento está en el plano cartesiano y se mueve horizontalmente, ¿cómo se calcula su distancia?
-La distancia se calcula como la longitud que existe desde un punto hasta otro en el plano cartesiano, sin importar la dirección de movimiento.
¿Qué fórmula se usa para encontrar el punto medio de un segmento en el plano cartesiano?
-El punto medio se calcula como el promedio de las coordenadas de x y el promedio de las coordenadas de y de los dos puntos extremos del segmento.
¿Qué es lo que determina el cálculo del punto medio y cómo se diferencia de la distancia?
-El cálculo del punto medio determina la coordenada en la que se encuentra el punto medio del segmento, mientras que la distancia da la longitud del segmento en unidades.
En el ejercicio presentado, ¿cuántos vértices tiene el triángulo y cómo se ubican en el plano cartesiano?
-El triángulo tiene tres vértices ubicados en las coordenadas (-2, 2), (13, -3) y (6, 6).
¿Cómo se calcula el punto medio de un segmento cuando se conocen las coordenadas de sus extremos?
-Para calcular el punto medio de un segmento, se suman las coordenadas de los extremos y se dividen por dos, tanto para las coordenadas x como para las y.
En el vídeo, ¿qué método se utiliza para determinar el perímetro total de un triángulo en el plano cartesiano?
-Para determinar el perímetro total de un triángulo, se calcula la distancia entre cada par de vértices y luego se suman todas las distancias obtenidas.
¿Cuál es la fórmula para calcular la distancia entre dos puntos en el plano cartesiano?
-La fórmula para calcular la distancia entre dos puntos (x1, y1) y (x2, y2) es √((x2 - x1)² + (y2 - y1)²).
En el caso de los segmentos con coordenadas que contienen radicales, ¿cómo se manejan las raíces en el cálculo del perímetro?
-Cuando las coordenadas de los segmentos contienen radicales, se dejan los términos con radicales como están y se utilizan para calcular el perímetro, aunque es común simplificar o usar una calculadora para obtener un valor decimal.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Convertir coordenadas cartesianas (rectangulares) a polares |👇👇video actualizado en la descripción👇👇

🟢 Distancia entre dos Puntos y Punto Medio✅ [EJERCICIOS RESUELTOS]

DISTANCIA ENTRE 2 PUNTOS EN LA CIRCUNFERENCIA

Punto medio entre dos puntos | Introducción
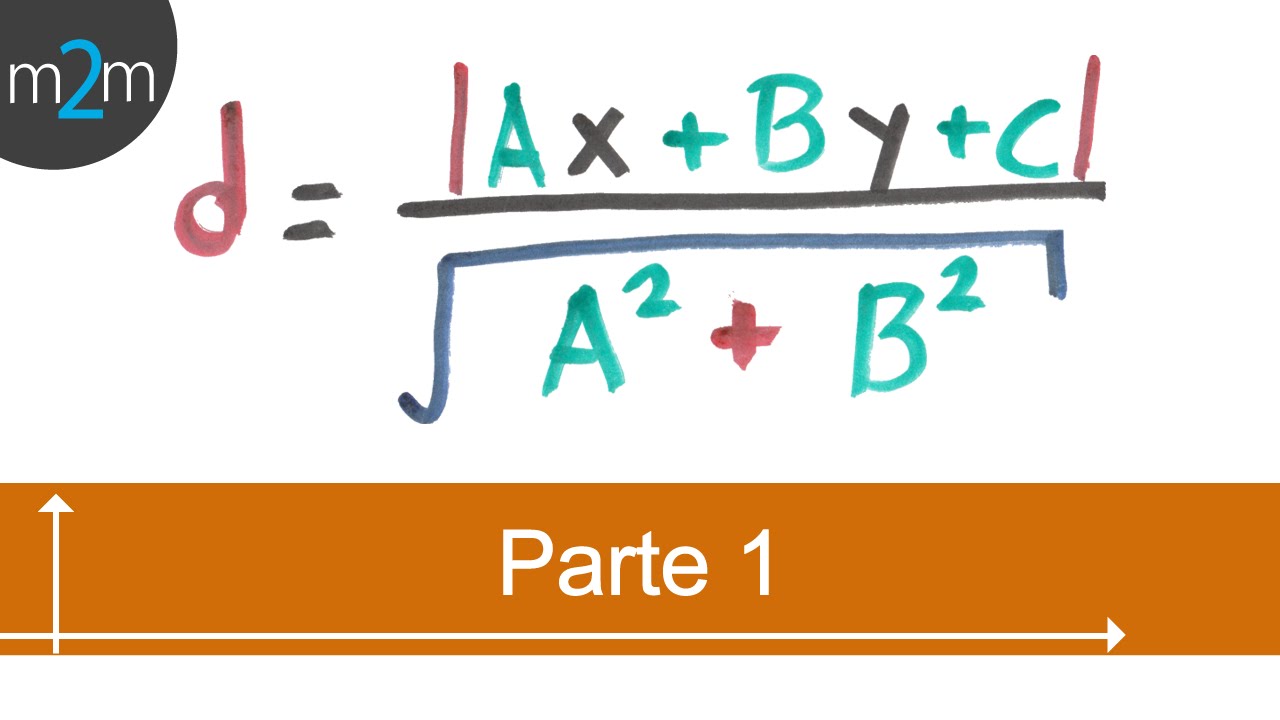
* Distancia entre un punto y una recta (PARTE 1)

Plano cartesiano introducción | Cómo dibujar el plano
5.0 / 5 (0 votes)
