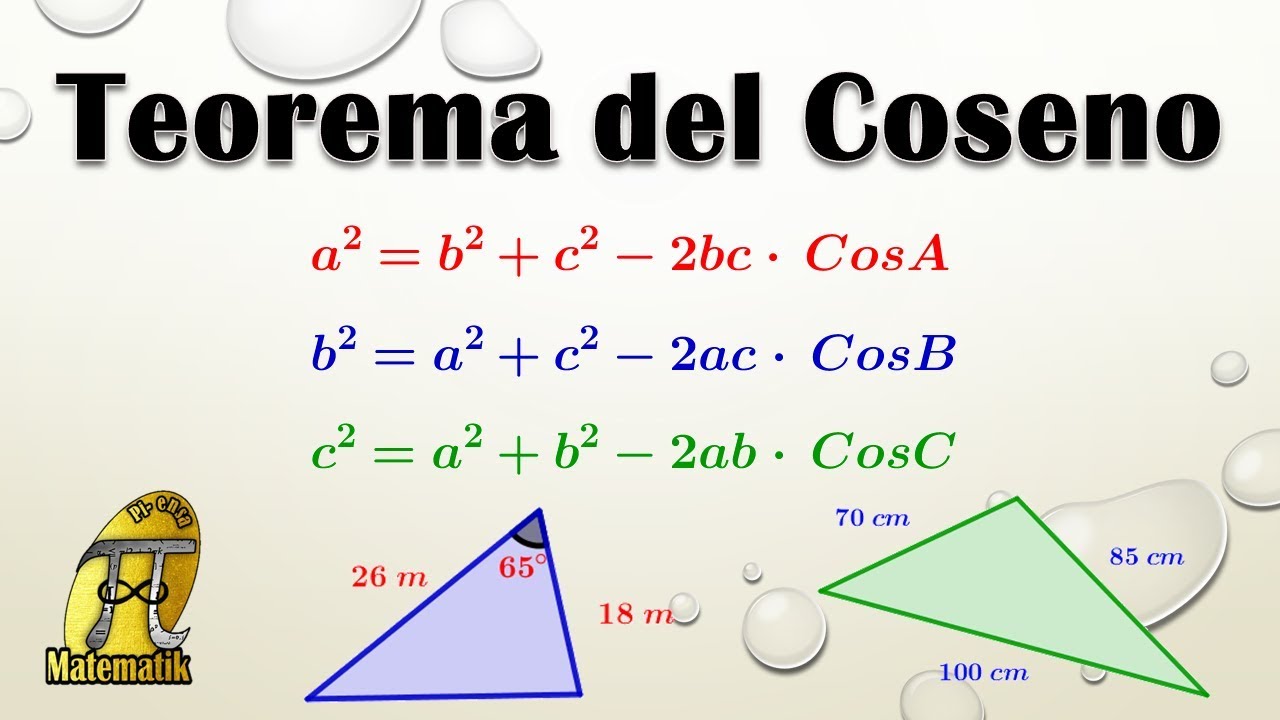
Ley de Senos | Introducción
Summary
TLDREl video ofrece una introducción al curso de la ley del seno y del coseno, explicando que esta ley se aplica en triángulos de cualquier tipo, especialmente en los que no son rectángulos. Se aclara que los ángulos en un triángulo suelen ser designados con letras mayúsculas (A, B, C) y los lados con minúsculas (a, b, c), siendo el lado opuesto al ángulo. La ley del seno se escribe como la relación del lado con el seno del ángulo opuesto, y se utiliza cuando se conoce una pareja (lado y ángulo) y algún otro dato. El video promete ejercicios prácticos en futuras sesiones y invita a suscriptores a interactuar y seguir el canal.
Takeaways
- 📚 La ley del seno se aplica a cualquier tipo de triángulo, especialmente en los que no son rectángulos.
- 🔢 En matemáticas, los ángulos de un triángulo generalmente se denotan con letras mayúsculas A, B y C, y los lados con las minúsculas a, b y c.
- 📐 La ley del seno relaciona el lado de un triángulo con el seno del ángulo opuesto a ese lado.
- 📝 La fórmula de la ley del seno se escribe como a/sen(A) = b/sen(B) = c/sen(C), pero se ajusta según los datos conocidos.
- 👉 La ley del seno es útil cuando se conoce una pareja de lado y ángulo, o cualquier otro dato adicional.
- 🔄 Aunque la ecuación completa de la ley del seno se puede escribir, en la práctica se utiliza solamente una parte de ella dependiendo de los datos disponibles.
- 📐 La ley del seno permite resolver problemas de triángulos cuando se conoce una pareja lado-ángulo y se busca encontrar otro lado o ángulo.
- ❗️ Es importante utilizar la parte correcta de la ecuación de la ley del seno en función de los datos que se conocen y los que se desean encontrar.
- 🎓 El video ofrece una introducción a la ley del seno y sugiere que hay más contenido disponible en el canal del presentador para aprender más sobre su aplicación.
- 👋 El presentador invita a los espectadores a suscribirse, comentar, compartir y dar like al vídeo para obtener más información sobre la ley del seno.
Q & A
¿Qué tipo de triángulos se pueden trabajar con la ley del seno?
-La ley del seno se puede aplicar a cualquier tipo de triángulo, aunque se utiliza especialmente en los triángulos oblicuángulos, es decir, aquellos que no son rectángulos.
¿Es necesario que los triángulos rectángulos usen la ley del seno?
-No, los triángulos rectángulos generalmente se trabajan con el teorema de Pitágoras o razones trigonométricas.
¿Cómo se designan los ángulos y los lados en un triángulo?
-Los ángulos se designan con letras mayúsculas (A, B, C), y los lados opuestos a estos ángulos se designan con letras minúsculas correspondientes (a, b, c).
¿Cómo se relaciona el seno de un ángulo con su lado opuesto?
-La ley del seno relaciona el lado de un triángulo con el seno del ángulo opuesto. Se puede expresar como: a/sin(A) = b/sin(B) = c/sin(C).
¿Es posible reorganizar la fórmula de la ley del seno?
-Sí, se puede escribir de otras formas, como colocando los senos de los ángulos en la parte superior y los lados en la inferior, por ejemplo: sin(A)/a = sin(B)/b = sin(C)/c.
¿Cuándo es útil aplicar la ley del seno?
-La ley del seno se utiliza cuando se conoce una pareja de datos (un ángulo y su lado opuesto) y algún otro dato adicional, como otro ángulo o lado.
¿Es necesario usar toda la ecuación de la ley del seno en un ejercicio?
-No, generalmente solo se usan dos partes de la ecuación, dependiendo de los datos que se conocen. Por ejemplo, se puede usar a/sin(A) = b/sin(B) si se conocen los valores correspondientes.
¿Qué significa conocer una 'pareja' en la ley del seno?
-Conocer una pareja significa saber el valor de un ángulo y su lado opuesto en el triángulo. Este par de datos es fundamental para aplicar la ley del seno.
¿Qué ocurre si se conoce una pareja y un dato adicional en un triángulo?
-Si se conoce una pareja y algún otro dato adicional (como otro ángulo o lado), se puede aplicar la ley del seno para resolver el triángulo.
¿Cuál es el objetivo del curso mencionado en el vídeo?
-El objetivo del curso es enseñar la ley del seno y del coseno, proporcionando una introducción teórica y ejercicios prácticos que ayudan a aplicar estos conceptos en diferentes tipos de triángulos.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)